
- •Свойства определителей
- •Ортогональность векторов.
- •11.Линейные операции в координатной форме
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •13 Вопрос
- •14 Вопрос
- •15 Вопрос
- •16 Вопрос
- •17. Свойства непрерывных на отрезке функций.
- •Определение производной; задачи, приводящие к понятию производной.
- •Геометрический и механический смысл производной функции.
- •Техника дифференцирования функций. Таблица производных
- •Дифференцируемость функции. Определение дифференциала функции.
- •Связь дифференциала с производной. Геометрический смысл дифференциала. Понятие дифференциала. Геометрический смысл дифференциала. Инвариантность формы первого дифференциала.
- •Основные теоремы дифференциального исчисления.
- •23. Основные теоремы дифференциального исчисления: Ферма, Ролля, Коши, Лагранжа
- •24. Условия возрастания и убывания функций. Стационарные точки.
- •25. Необходимые и достаточные признаки максимума и минимума.
- •26. Отыскание наибольшего и наименьшего значений непрерывной на отрезке функции.
- •27. Исследование на максимум и минимум с помощью производных второго порядка.
- •28. Асимптоты графиков функции
- •29. Исследование функций на выпуклость и вогнутость. Точки перегиба
- •30. Алгоритм общего исследования функции с помощью производных, построение графика.
13 Вопрос
Бесконечно малые функции
Функция f (x) называется бесконечно малой функцией в точке х = х0, если
![]()
Аналогично определяются бесконечно малые функции при x → ∞, x → + ∞, x → – ∞, x → x0 – 0, x → x0 + 0. Можно дать равносильное определение бесконечно малой функции «на языке ε – δ: функция f (x) называется бесконечно малой в точке х = х0, если для любого как угодно малого ε > 0 существует δ = δ(ε) > 0, такое, что для всех х, удовлетворяющих неравенству 0 < | х – x0 | < δ, выполняется неравенство | f (x) | < ε. Или в символьном виде
(![]() ε > 0) (
ε > 0) (
![]() δ
= δ(ε) > 0)(
0
< |х
– х0|
< δ ) : | f
(x)
| < ε.
δ
= δ(ε) > 0)(
0
< |х
– х0|
< δ ) : | f
(x)
| < ε.
Бесконечно большие функции
Функция f (x) называется бесконечно большой функцией в точке х = x0 (или x → x0), если для любого как угодно большого положительного числа K > 0 существует δ = δ(K) > 0, такое, что для всех х, удовлетворяющих условию 0 < | x – х0 | < δ , выполняется неравенство | f (x) | > К. В этом случае пишут
![]()
и говорят, что функция стремится к бесконечности при х → х0 , или что она имеет бесконечный предел в точке х = х0. Если же в определении выполняется неравенство f (x) > K (f (x) < – K) , то пишут
![]() или
или
![]()
и говорят, что функция имеет в точке х0 бесконечный предел, равный + ∞ (– ∞). По аналогии с конечными односторонними пределами определяются и бесконечные односторонние пределы:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Так, например, пишут если для любого как угодно большого положительного числа K > 0 существует δ = δ(K) > 0, такое, что для всех х, удовлетворяющих условию х0 < x < х0 + δ , выполняется неравенство f (x) > К. Или в символической записи
( K > 0) ( δ = δ(K)> 0)( x0 < х < x0+δ ) : f (x) > K.
Предлагается самостоятельно сформулировать определение бесконечно большой функции при x → + ∞, x → – ∞.
14 Вопрос
Свойства бесконечно малых функций
Опираясь на правила вычисления пределов, можно сформулировать свойства бесконечно малых: алгебраическая сумма и произведение конечного числа бесконечно малых функций при x → x0, а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при x → x0:
1. |
|
2. |
|
3. |
|
4. |
|
Все сказанное о бесконечно малых функциях при x → x0 справедливо и для бесконечно малых функций при x → ∞, x → + ∞, x → – ∞, x → x0 – 0, x → x0 + 0.
15 Вопрос
Сравнение бесконечно малых функций
Пусть α(x) и β(x) две бесконечно малые функции при x → x0 и β(x) отлична от нуля в некоторой окрестности точки х0 (за исключением, быть может, самой точки х0). Если
![]() =
0,
=
0,
то α(x) называется бесконечно малой более высокого порядка, чем β(x) . В этом случае пишут α(x) = o(β(x)) и говорят α(x) есть о − малое от β(x). Если
= А ≠ 0 ( A - число),
то бесконечно малые α(x) и β(x) имеют одинаковый поряок малости. В этом случае пишут α(x) = O(β(x)), (α(x) есть O - большое от β(x). Если
= ∞,
то α(x) называется бесконечно малой более низкого порядка, чем β(x). Если
= 1,
то α(x) и β(x) называется эквивалентными бесконечно малыми, α(x) ~ β(x). В некоторых случаях недостаточно знать, что одна из двух бесконечно малых является бесконечно малой более высокого порядка, чем другая. Нужно еще оценить, как высок этот порядок. Поэтому вводится следующее правило: если
![]() ,
,
то α(x) является бесконечно малой n -го порядка относительно β(x).
Таблица эквивалентных бесконечно малых функций
Так как
 ,
то в точке х
= 0 имеем sin x
~ x,
и в этом случае имеет место равенство
sin x = x
+ o(x).
,
то в точке х
= 0 имеем sin x
~ x,
и в этом случае имеет место равенство
sin x = x
+ o(x).
Так как
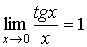 ,
то в точке х
= 0 имеем tg x
~ x,
и в этом случае имеет место равенство
tg x = x
+ o(x).
,
то в точке х
= 0 имеем tg x
~ x,
и в этом случае имеет место равенство
tg x = x
+ o(x).
Так как
 ,
то в точке х
= 0 имеем arcsin x
~ x,
и в этом случае имеет место равенство
arcsin x = x
+ o(x).
,
то в точке х
= 0 имеем arcsin x
~ x,
и в этом случае имеет место равенство
arcsin x = x
+ o(x).
Так как
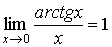 ,
то в точке х
= 0 имеем arctg x
~ x,
и в этом случае имеет место равенство
arctg x = x
+ o(x).
,
то в точке х
= 0 имеем arctg x
~ x,
и в этом случае имеет место равенство
arctg x = x
+ o(x).
Так как
![]() ,
то
,
то
![]() ,
и в этом случае имеет место равенство
,
и в этом случае имеет место равенство
![]()
В точке х = 0 многочлен эквивалентен своему моному младшей степени
![]() .
.
Поэтому при х
= 0 имеем
![]() .
Использование
теоремы о замене функции на эквивалентную
под знаком предела упрощает вычисление
предела. Например,
.
Использование
теоремы о замене функции на эквивалентную
под знаком предела упрощает вычисление
предела. Например,
![]() .
.
Так как
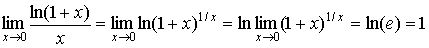 ,
то ln (1 + x)
~ x,
,
то ln (1 + x)
~ x,
и в этом случае имеет место равенство ln (1 + x) = x + o(x).
Так как
 ,
то
,
то
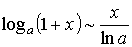
 .
.
Так как
 ,
то ex
~ 1 + x,и
в этом случае имеет место равенство
,
то ex
~ 1 + x,и
в этом случае имеет место равенство
ex ~ 1 + x + o(x).
В случае натурального k имеем

поэтому для
натурального k
имеем
![]() ,
и в этом случае имеет место равенство
,
и в этом случае имеет место равенство
(1 + x)k = 1 + k·x + o(x)
Так как
![]() ,
то ax
~ 1 + x·ln
a,
и в этом случае имеет место равенство
ax
~ 1 + x·ln
a
+ o(x)
,
то ax
~ 1 + x·ln
a,
и в этом случае имеет место равенство
ax
~ 1 + x·ln
a
+ o(x)
Так как
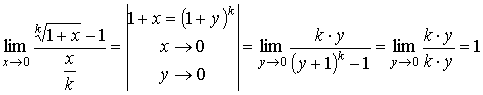 ,
то
,
то
![]() ,
и в этом случае имеет место равенство
,
и в этом случае имеет место равенство
![]()
