1. Предмет теории вероятностей, два признака случайного явления, постулат теории вероятностей. Примеры построения пространств элементарных исходов.

Предметом теории вероятностей является математический анализ случайных явлений, т. е. таких эмпирических феноменов, которые - при заданном комплексе условий — могут быть оха­рактеризованы тем, что

Для них отсутствует детерминистическая регулярность (наблюдения над ними не всегда приводят к одним и тем же исходам)

и в то же самое время

Они обладают некоторой статистической регулярностью (проявляющейся в статистической устойчивости частот).

Поясним сказанное на классическом примере «честного» подбрасывания «правильной» монеты. Ясно, что заранее невоз­можно с определенностью предсказать исход каждого подбрасы­вания. Результаты отдельных экспериментов носят крайне не­регулярный характер (то «герб», то «решетка») и кажется, что это лишает нас возможности познать какие-либо закономерно­сти, связанные с этими экспериментами. Однако, если провести большое число «независимых» подбрасываний, то можно заме­тить, что для «правильной» монеты будет наблюдаться вполне определенная статистическая регулярность, проявляющаяся в том, что частота выпадания «герба» будет «близка» к Уг.

Статистическая устойчивость частот делает весьма правдопо­добной гипотезу о возможности количественной оценки «случай­ности» того или иного события А, осуществляемого в резуль­тате экспериментов. Исходя из этого, теория вероятностей посту­лирует существование у события Л определенной числовой характеристики Р (А), называемой вероятностью этого события, естественное свойство которой должно состоять в том, что с ростом числа «независимых» испытаний (экспериментов) часто­та появления события А должна приближаться к Р (А).

Применительно к рассмотренному примеру это означает, что вероятность события Л, состоящего в выпадании «герба» при бросании «правильной» монеты, естественно считать равной 1/2.

2+3.Вероятностная модель эксперимента с конечным числом исходов

1. Рассмотрим некоторый эксперимент, все мыслимые исходы которого описываются конечным числом различных исходов ω₁…ω_N. Для нас несущественна реальная природа этих исхо­дов, важно лишь то, что их число N конечно.

Исходы ω₁…ω_N - будем называть элементарными событиями, а их совокупность

Ω = { ω₁…ω_N }

(конечным) пространством элементарных событий или простран­ством исходов.

Выделение пространства элементарных событий представляет собой первый шаг в формулировании понятия вероятностной модели того или иного эксперимента.

«Вероятностное пространство в задаче выбора с возвращением: набор упорядоченный и неупорядоченный.»

2. Пример 4. Выбор с возвращением. Так называют экспе­римент, в котором на каждом шаге извлеченный шар возвращается обратно. В этом случае каждая выборка из п шаров может быть записана в виде (а₁ ..., а_п), где а_i— номер шара, извлеченного на i-м шаге. Понятно, что в случае выбора с возвращением каж­дое а_i может принимать любое из М значений 1, 2, ..., М. Описание пространства элементарных сооытнй существенно зави­сит от того, считаем ли мы выборки тождественного состава такие, как, скажем, (4, 1, 2, 1) и (1, 4, 2, 1), различными или одинаковыми. В связи с этим принято различать два случая: упорядоченные выборки и неупорядоченные выборки. В первом случае выборки, состоящие из одних и тех же элементов, но отличающиеся порядком следования этих элементов, объявляются различными. Во втором случае порядок следования элементов не принимается во внимание и такие выборки объявляются тождест­венными. Чтобы подчеркнуть, какие конкретно выборки мы рас­сматриваем, будем для упорядоченных выборок использовать обозначение (a₁ ..., а_n), а для неупорядоченных — [a₁ ..., а_n].

Итак, в случае упорядоченных выборок пространство элемен­тарных событий □ имеет следующую структуру:

Ω = {ω: ω = (а₁, ..., а_п), а₁ =1, ..., М}

и число (различных) исходов

N(Ω ) = Mⁿ (1)

Если же рассматриваются неупорядоченные выборки, то Ω = {ω: ω = (а₁, ..., а_п), а₁ =1, ..., М}.

Понятно, что N (Ω) (различных) неупорядоченных выборок меньше, чем число упорядоченных. Покажем, что для этого случая

N (Ω) =Cⁿ_M +n-1, (2)

где С_k^l = 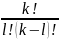число сочетаний из k элементов по l.

Будем вести доказательство по индукции. Обозначим N (М, п) число интересующих нас исходов.

Ясно, что для всех k≤М

N(k, l) = k = С_k^l.

Предположим теперь, что N (k,n) =C^k_k+n-1, k≤М, и покажем,

что эта формула остается справедливой при замене n на n+1.

При рассмотрении неупорядоченных выборок [a₁,…,a_n+1] можно считать, что их элементы расположены в порядке неубывания: a₁≤a₂≤ а_п+1. Очевидно, что число неупорядоченных выборок с а₁=1 равно N (М, п), с а_х = 2 равно N(М —1, п) и т. д. Сле­довательно,

N(М, п + 1) = N(М, п) + N{М- 1, п) + ... + N(1, п) =

=Cⁿ_M+n-1+ Cⁿ_M-1+n-1+…+C_nⁿ⁼

=(C_M+nⁿ⁺¹- C_M+nⁿ⁺¹-1)+( C_M-1-nⁿ⁺¹- C_M-1+n-1ⁿ⁺¹)+…+(C_n+1ⁿ⁺¹-C_nⁿ)+ C_nⁿ=C_M+nⁿ⁺¹

где мы воспользовались следующим легко проверяемым свойством биномиальных коэффициентов:

C_k^l-1+ C_k^l= C_k^l_+1.

«Вероятностное пространство в задаче выбора без возвращения: набор упорядоченный и неупорядоченный.»

Пример 5. Выбор без возвращения. Будем предполагать, что n≤M и что извлеченные шары обратно не возвращаются. В этом случае также рассматриваются две возможности, связанные с раз­личением упорядоченных и неупорядоченных выборок.

В случае упорядоченных выборок без возвращения простран­ство исходов

Ω = {ω: ω = (а₁, ..., а_п), a₁≠a₂≠a_n,a_i= 1, .... М},

а число элементов этого множества (называемых размещениями) равно М (М — 1)... (М — п + 1). Для этого числа используется обозначение (М)_п, или Ам, называемое «числом размещений из М по n».

В случае неупорядоченных выборок (называемых сочетаниями) пространство исходов

Ω = {ω: ω = [a₁, ..., a_n], a₁≠a₂≠a_n,a_i= 1, .... М},

состоит из

N(Ω)=C_Mⁿ (3)

элементов. Действительно, из каждого неупорядоченного набора [a₁, ..., a_n], состоящего из различных элементов, можно получить ровно n! упорядоченных наборов. Следовательно,

N(Ω)*n!=(M)_n

и, значит, N(Ω)=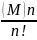 =C_Mⁿ

Результаты о числе исходов в случае п извлечений из урны с М шарами сведем в табл. 1.

Таблица 1

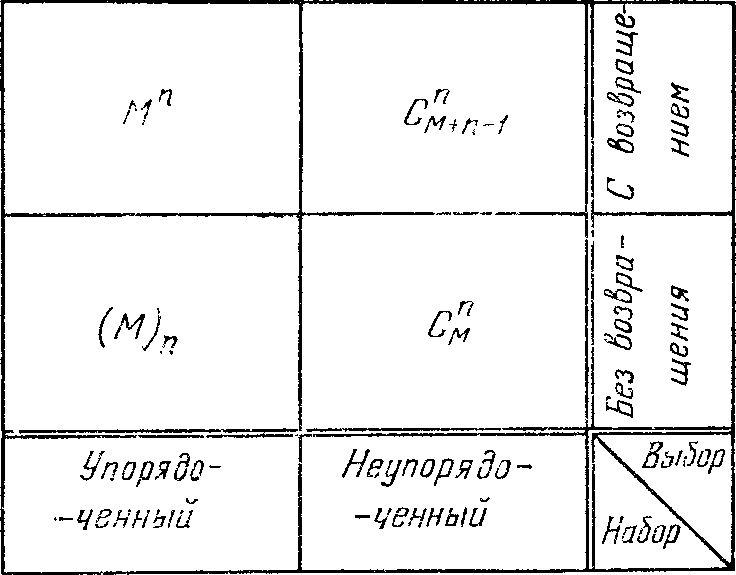
Для случая М = 3 и п = 2 структура соответствующих пространств элементарных событий приводится в табл. 2.

Таблица 2

4+5. «Вероятностное пространство в задаче размещения различных частиц по уровням: размещение с запретом и без запрета. Статистика Максвелла-Больцмана.»

«Вероятностное пространство в задаче размещения различных частиц по уровням: размещение с запретом и без запрета. Статистика Бозе-Энштейна и Ферми-Дирака.»

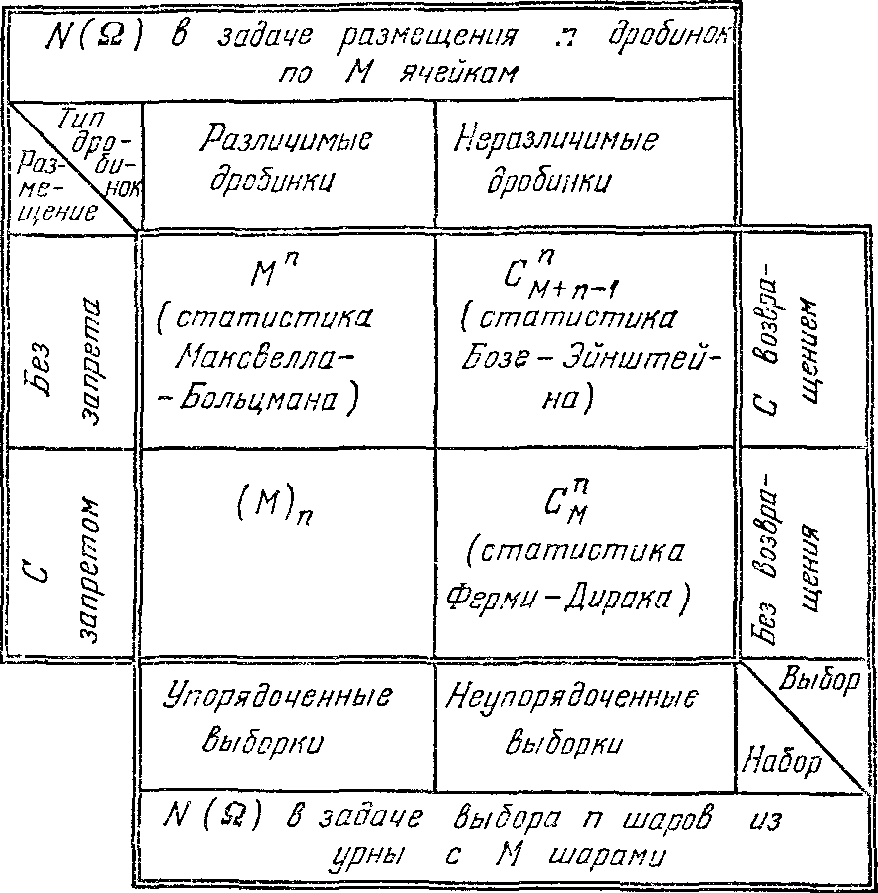
Пример 6. Размещение дробинок по ячейкам.. Рассмотрим вопрос о структуре пространства элементарных событий в задаче размещения n дробинок (шаров и т. п.) по M ячейкам (ящикам и т. п.). В статистической физике подобная задача возникает, например, при изучении распределения п частиц (это могут быть протоны, электроны, ...) по М состояниям (это могут быть энер­гетические уровни).

Пусть ячейкам присвоены номера 1, 2, ..., М, и предположим сначала, что дробинки различимы (имеют номера 1, 2, ..., п). Тогда распределение n дробинок по М ячейкам полностью опи­сывается (упорядоченным) набором (а₁, ..., а_п), где а_{i— номер ячейки, куда попала дробинка с номером i. Если же рассматри­ваемые дробинки неразличимы, то их распределение по М ячей­кам полностью описывается (неупорядоченным) набором [а₁,…,a_n], где а_i — номер ячейки, в которую попала дробинка на i-м шаге.

Сравнивая рассматриваемую ситуацию с примерами 4 и 5, видим, что имеют место следующие соответствия:

(упорядоченные выборки)↔ (различимые дробинки),

(,неупорядоченные выборки)↔ (неразличимые дробинки),

означающие, что случаю упорядоченных (неупорядоченных) выбо­рок в задаче выбора п шаров из урны с М шарами соответствует (один и только один) случай расположения различимых (неразли­чимых) дробинок в задаче размещения п дробинок по М ячейкам.

Аналогичный смысл имеют также следующие соответствия;

(выбор с возвращением)↔( в ячейке может находиться любое число дробинок),

(выбор без возвращения) ↔(в ячейке может находиться не более одной дробинки)

Из этих соответствий можно сконструировать соответствия типа:

(неупорядоченные выборки, (неразличимые дробинки в задаче их размещения по ячейкам, когда в каждой

е задаче выбора без возвращения)↔ из них не может находиться более одной дробинки)

и т. д., что дает возможность использовать примеры 4 и 5 для описания структуры пространства элементарных событий в задаче распределения различимых и неразличимых дробинок по ячейкам с запретом (в ячейке может находиться не более одной дробинки) или без запрета (в ячейке может находиться любое число дро­бинок).

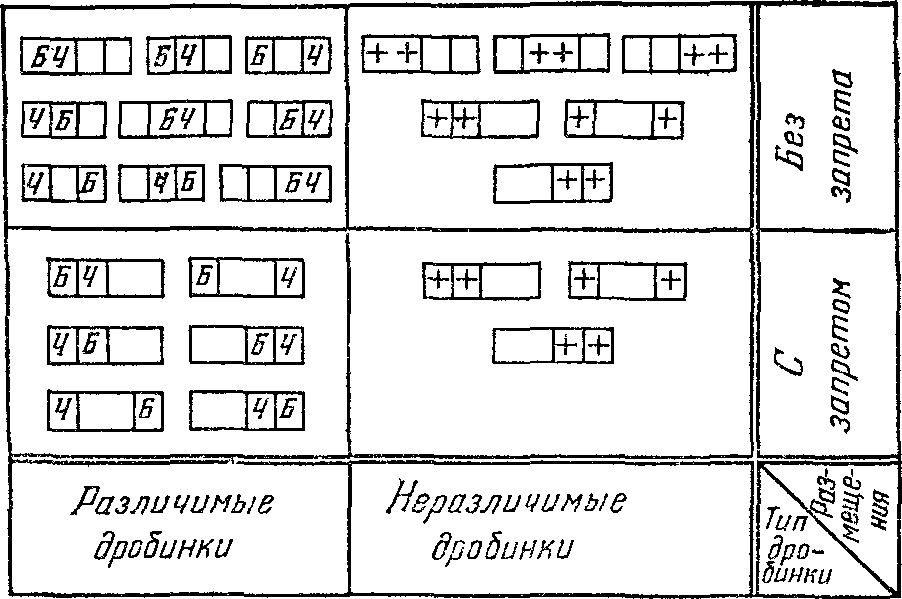
Табл. 3 показывает структуру расположения двух дробинок по трем ячейкам. В случае различимых дробинок они обозна­чаются Б (белая) и Ч (черная). В случае неразличимых дробинок их наличие в ячейке обозначается знаком +.

Указанная выше двойственность между рассматриваемыми задачами позволяет очевидным образом найти число исходов в задаче размещения дробинок по ячейкам. Соответствующие результаты, включающие в себя также и результаты табл. 1, сведены в табл. 4.

В статистической физике говорят, что различимые (неразли­чимые) частицы, не подчиняющиеся принципу запрета Паули, удовлетворяют (физической) статистике Максвелла — Больцмана (соответственно — статистике Бозе—Эйнштейна). Если же частицы неразличимы и подчиняются принципу запрета, то —статистике Ферми —Дирака (см. табл. 4). Известно, например, что электроны,

протоны и нейтроны подчиняются статистике Ферми — Дирака. Фотоны и пи-мезоны — статистике Бозе —Эйнштейна. Известно также, что случай различимых частиц, подчиняющихся принципу запрета, в физике не встречается.

Таблица 3

6. Понятие случайного события, операции над событиями.

Случайным событием или просто событием будем на­зывать любое подмножество множества Ω, если Ω конечно или счетно:

Ω = {ω₁, ω₂, . . ω_N} или Ω = {ω₁, ω₂, . . ω_n….}

В случае произвольного Ω событиями будем называть только подмножества из некоторого класса ϗ подмножеств Ω, который будет определен после введения опе­раций над событиями, совпадающих с операциями над множествами.

Суммой двух событий А и В назовем событие А + В (или АU В), состоящее из всех элементарных событий, принадлежащих по крайней мере одному из событий А или В. Можно сказать, что в реальном опыте событие, соответствующее А + В_, состоит в том, что произошло по крайней мере одно из событий А или В. Пусть в при­мере 5 из § 1 событиями А и В являются попадания соответственно в большой и малый круг (рис. 1) . Тогда событием А + В является заштрихованная область на рис. 1, а.

Произведением АВ (или А ∩ B называется событие, состоящее из элементарных событий, принадлежащих и А и В. Событие А В происходит тогда и только тогда, когда происходит и А и В. Для примера 5 событие А В изображено заштрихованной фигурой на рис* 1, б*

Разностью А \ В называется событие, состоящее из элементов множества А, не принадлежащих В (см. рис. 1_А в)_Ф

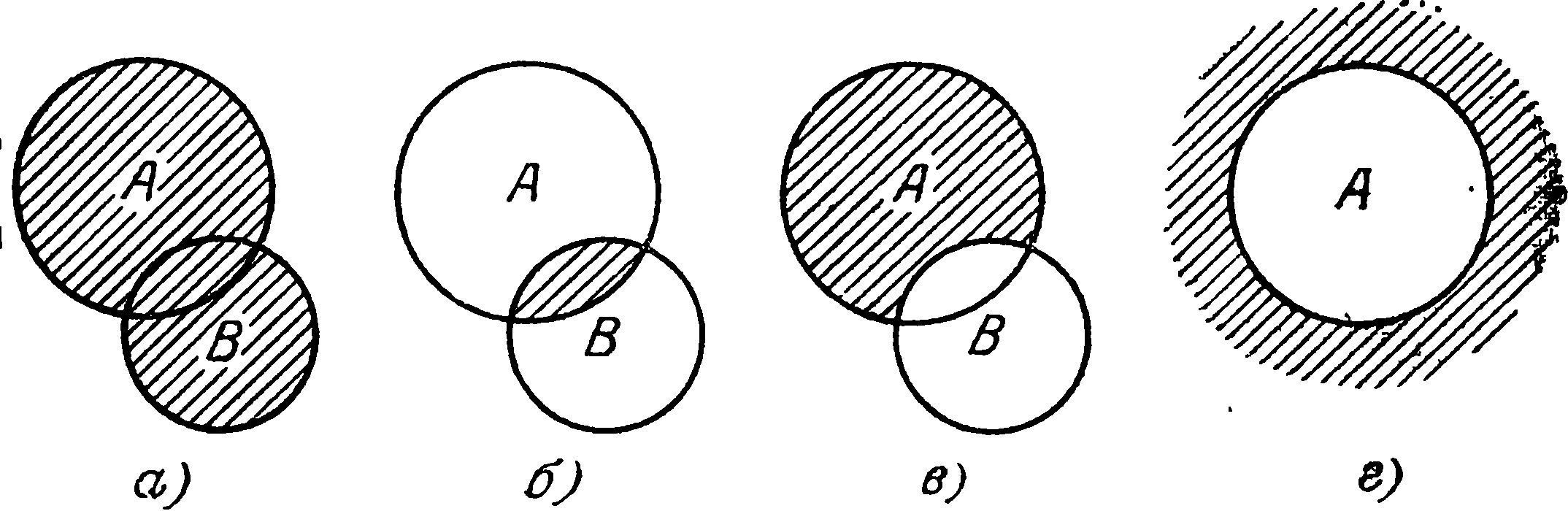
9. Определение вероятностной меры, вероятность суммы событий (для несовместных и произвольных событий). Общая формула.

Припишем каждому элемен­тарному событию (исходу) ω_iϵΩ, i=1,…, N, некоторый «вес», обозначаемый

р (ω_i), и называемый вероятностью исхода ω_i, кото­рый будем считать удовлетворяющим следующим условиям:

1. 0 ≤ р (ω_i) ≤1 (неотрицательность),

2. р (ω_i) +…+ р (ω_N) = 1 (нормированность).

Отправляясь от заданных вероятностей р (ω_i) исходов ω_i, опре­делим вероятность Р (А) любого события АϵǍ по формуле:

Наконец, скажем, что тройка

(Й, Р),

где Ω = { ω₁…ω_N }, Ǎ— некоторая алгебра подмножеств Ω, Р = {Р(A); A ϵ Ǎ}определяет (задает) вероятностную модель, или вероятностное пространство, эксперимента с (конечным) про­странством исходов ω и алгеброй событий Ǎ.

Перечислим очевидные в случае дискретного пространства свойства вероятности, которые мы скоро докажем сразу в общем случае.

1. 

  ;   ;   ;

2.  

Если   и   несовместны, то  ;

3.  

В общем случае  ;

4.  

Если  , то  .

(Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим. Далее укажем слабые стороны этого определения и приведем другие определения, позволяющие преодолеть недостатки классического определения.

Рассмотрим пример. Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них - красные, 3 - синие и 1 - белый. Очевидно, возможность вынуть наудачу из урны цветной (т. е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.

Поставим перед собой задачу дать количественную оценку возможности того, что взятый наудачу шар цветной. Появление цветного шара будем рассматривать в качестве события А. Каждый из возможных результатов испытания (испытание состоит в извлечении шара из урны) назовемэлементарным исходом (элементарным событием). Элементарные исходы обозначим через w₁, w₂, w₃ и т.д. В нашем примере возможны следующие 6 элементарных исходов: w₁ - появился белый шар; w₂, w₃ - появился красный шар; w₄, w₅, w₆ - появился синий шар. Легко видеть, что эти исходы образуют полную группу попарно несовместных событий (обязательно появится только один шар) и они равновозможны (шар вынимают наудачу, шары одинаковы и тщательно перемешаны).

Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию. В нашем примере благоприятствуют событию A (появлению цветного шара) следующие 5 исходов: w₂, w₃, w₄, w₅, w₆.

Таким образом, событие А наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих A; в нашем примере А наблюдается, если наступит w₂, или w₃, или w₄, или w₅, или w₆. В этом смысле событие А подразделяется на несколько элементарных событий (w₂, w₃, w₄, w₅, w₆); элементарное же событие не подразделяется на другие события. В этом состоит различие между событием А и элементарным событием (элементарным исходом).

Отношение числа благоприятствующих событию А элементарных исходов к их общему числу называют вероятностью события А и обозначают через Р (А). В рассматриваемом примере всего элементарных исходов 6; из них 5 благоприятствуют событию А. Следовательно, вероятность того, что взятый шар окажется цветным, равна Р (A) = 5 / 6. Это число и дает ту количественную оценку степени возможности появления цветного шара, которую мы хотели найти. Дадим теперь определение вероятности.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой

Р (A) = m / n,

где m - число элементарных исходов, благоприятствующих A; n - число всех возможных элементарных исходов испытания.

Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу. Из определения вероятности вытекают следующие ее свойства:

С в о й с т в о 1. Вероятность достоверного события равна единице.

С в о й с т в о 2. Вероятность невозможного события равна нулю.

С в о й с т в о 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.)

10. Определение вероятностной меры, примеры классической и геометрической вероятностей.

Классическое определение вероятности

Предположим, что мы имеем дело с пространством элементарных исходов, состоящим из конечного числа N элементов: Ω = {ω_1, ω₂, … ω_N}. Более того, предположим, что из каких-либо соображений мы можем считать элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной 1/ N.

Эти соображения чаще всего не имеют отношения к математической модели и основаны на какой-либо симметрии в эксперименте (симметричная монета, хорошо перемешанная колода карт, правильная кость). Либо мы можем заранее считать исходы эксперимента равновозможными, но тогда рано или поздно все равно возникнет вопрос о соответствии такой математической модели реальному эксперименту.

Если событие А = {} состоит из k элементарных исходов, то вероятность этого события равняется

отношению k / N:

где символом │А│ обозначено число элементов конечного множества А.

Определение 7.

Говорят, что эксперимент удовлетворяет классическому определению вероятности (или классической вероятностной схеме), если пространство элементарных исходов состоит из конечного числа │А│ = Nравновозможных исходов.

В этом случае вероятность любого события А вычисляется по формуле

называемой классическим определением вероятности. Эта формула читается так: «вероятность событияА равна отношению числа исходов, благоприятствующих событию А, к общему числу исходов».

Пример 6. Рассмотрим, скажем, выбор двух шариков из двух или, что то же самое, дважды подбросим монету. Если учитывать порядок, то исходов получится 4, и все они равновозможны, то есть имеют вероятность по 1/4:

(герб, герб), (решка, решка), (решка, герб), (герб, решка).

Если порядок не учитывать, то следует объявить два последних исхода одним и тем же результатом эксперимента, и получить три исхода вместо четырех: выпало два герба, либо две решки, либо один герб и одна решка.

При этом первые два исхода имеют вероятность 1/4, а последний — вероятность 1/4+1/4=1/2.

Геометрическая вероятность

2.1 Что это такое

Рассмотрим какую-нибудь область Ω в R^m ,(на прямой, на плоскости, в пространстве). Предположим, что «мера» Ω (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а. Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть А Í Ω не зависит от формы или расположения А внутри Ω, а зависит лишь от «меры» области.

Определение 9. Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можно изобразить точками некоторой области Ω в R^m так, что вероятность попадания точки в любую А Í Ω не зависит от формы или расположения А внутри Ω, а зависит лишь от меры области А (и, следовательно, пропорциональна этой мере):

«Мерой» мы пока будем называть длину, площадь, объем и т.д.

Если для точки, брошенной в область Ω, выполнены условия геометрического определения вероятности, то говорят, что точка равномерно распределена в области Ω.

Пример 8. Точка наудачу бросается на отрезок [0,1]. Вероятность точке попасть в точку {0,5} равна нулю, так как мера множества, состоящего из одной точки («длина точки»), есть 0. Вместе с тем попадание в точку {0,5} не является невозможным событием — это один из элементарных исходов эксперимента.

13. Определение условной вероятности, ее свойства.

Вероятность появления события  А  при условии, что событие  В  произошло, называется  условной вероятностью события  А  и вычисляется по формуле:

                                       

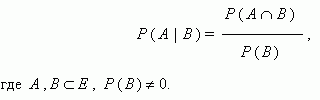
События  А , В   Е называются независимыми, если  Р ( А   В ) = Р ( А ) · Р ( В ) .

В противном случае события  А и В называются зависимыми.

15. Полная группа событий, формула полной вероятности.

Определение 21. Конечный или счётный набор попарно несовместных событий   таких, что   для всех   и  , называется полной группой событий или разбиением пространства  .

События  , образующие полную группу событий, часто называют гипотезами. При подходящем выборе гипотез для произвольного события   могут быть сравнительно просто вычислены   (вероятность событию   произойти при выполнении «гипотезы»  ) и собственно   (вероятность выполнения «гипотезы»  ). Как, используя эти данные, посчитать вероятность события  ?

Теорема 8  (формула полной вероятности). Пусть   — полная группа событий. Тогда вероятность любого события   может быть вычислена по формуле:

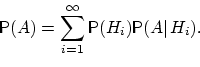
Доказательство. Заметим, что

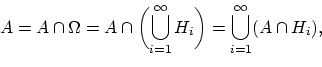
и события  ,   попарно несовместны. Поэтому

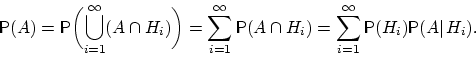
Во втором равенстве мы использовали  -аддитивность вероятностной меры (а что это?), а в третьем — теорему 6 умножения вероятностей.

16. Полная группа событий, понятие априорной и апостериорной вероятностей, теорема Байеса.

Априорные величины

Для вычисления относительной апостериорной вероятности для некоторой сети необходимо определить априорную структуру сети   и априорные параметры распределения  .

17) Определение n независимых в совокупности событий. Доказать, что из по парной независимости не следует независимость в совокупности.