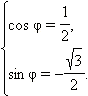2. Скалярное произведение, его геометрический смысл и вычисление:

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю

2. Угол между прямыми на плоскости:

Определение: Если заданы две прямые y = k₁x + b₁,  y = k₂x + b₂, то острый угол между этими прямыми будет определяться как:

Две прямые параллельны, если k₁ = k₂.

Две прямые перпендикулярны, если k₁ = -1/k₂.

Теорема: Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = А, В₁ = В. Если еще и С₁ = С, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы  уравнений этих прямых

2. Найти:

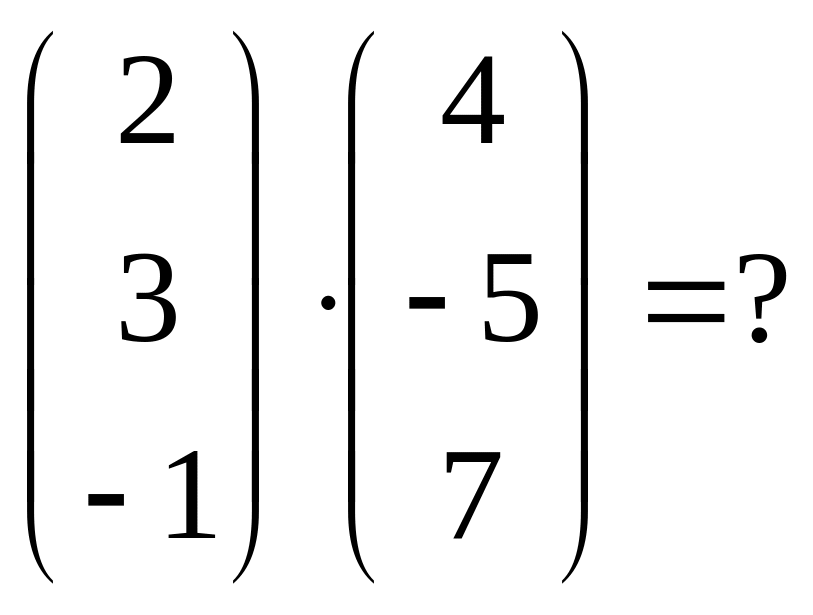
Решение:

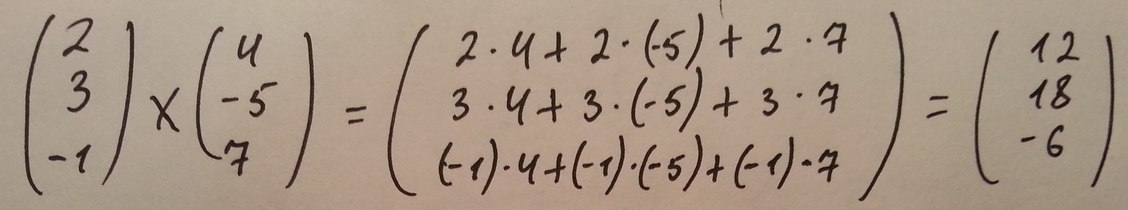
2. Найти угол между :

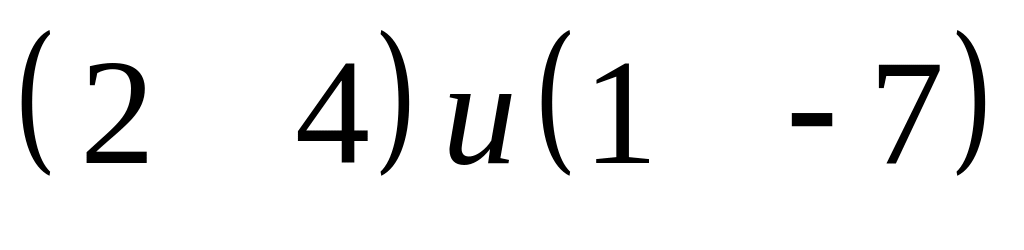Решение:

2. Тригонометрическая форма комплексного числа :

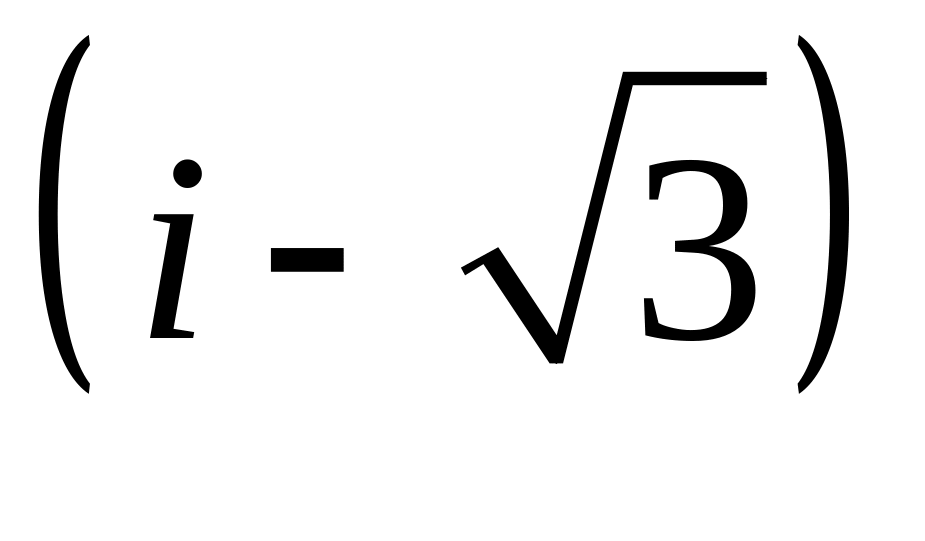Найдём модуль этого числа:   Аргумент данного числа находится из системы:

Значит, один из аргументов числа   равен   

Получаем:

Ответ: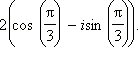 

2. Тригонометрическая форма комплексного числа :

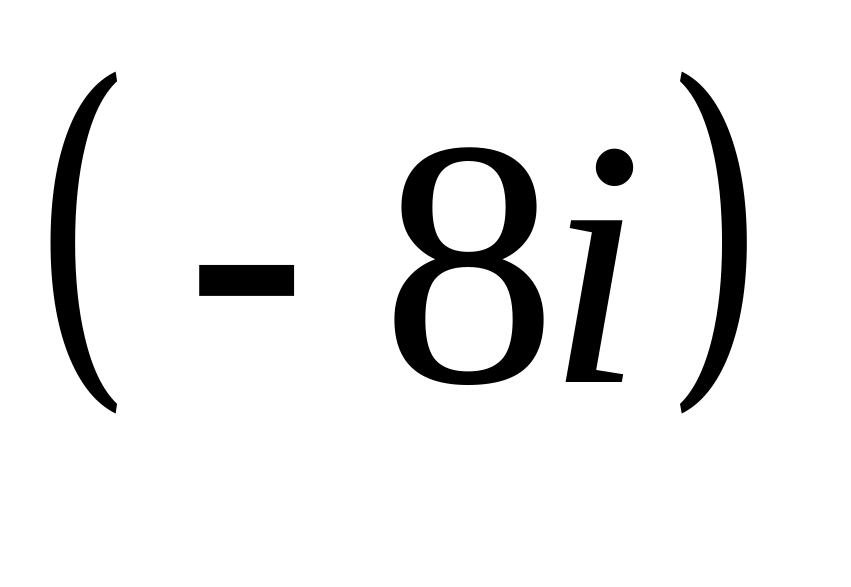Ответ: 8 • [ cos ( 270° 0´ 0˝ ) + i • sin ( 270° 0´ 0˝ ) ]

2. Параметрическое уравнение прямой, проходящей через точки :

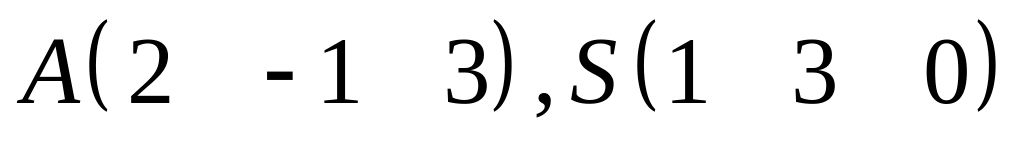2. Виды уравнений прямой по плоскости:

Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

•  C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

•  А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

•  В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

•  В = С = 0, А ≠0 – прямая совпадает с осью Оу

•  А = С = 0, В ≠0 – прямая совпадает с осью Ох

Уравнение прямой может быть представлено в различном виде в зависимости, от каких – либо заданных начальных условий.

2. Найти нормаль к плоскости :

2. В кубе A,B,C,D, A1,B1,C1,D1; AA1 = i; AB = j; AD = k. Найти AB; AA1; AC1 A1D:

Решение:

2. Найти матрицу поворота на угол 60 градусов:

Решение:

2. Найти ранг матрицы :

Решение:

Ваша матрица

№	A1	A2	A3	A4
1	3	0	-4	0
2	2	1	0	3
3	0	0	3	3
4	1	0	2	2

Занулили элементы в 1-ом столбце под 1-ым элементом

№	A1	A2	A3	A4
1	3	0	-4	0
2	0	1	8/3	3
3	0	0	3	3
4	0	0	10/3	2

Занулили элементы в 3-ем столбце под 3-им элементом

№	A1	A2	A3	A4
1	3	0	-4	0
2	0	1	8/3	3
3	0	0	3	3
4	0	0	0	-4/3