2. Свойства определителей:

1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером.

2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1.

3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

4. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

5. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же.

2. Геометрический смысл определителей:

Если есть векторы с координатами (Ax, Ay) и (Вх, Ву), то площадь параллелограмма, построенного на этих векторах, равна определителю матрицы, столбцами которой являются эти векторы.

2. Правило Крамера:

Система линейных уравнений:

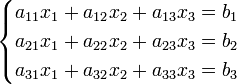
Определители:

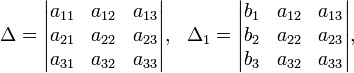
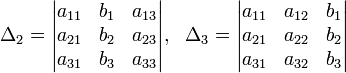
Решение:

Пример:

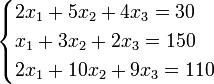
Определители:

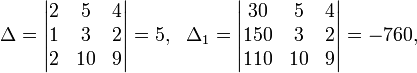
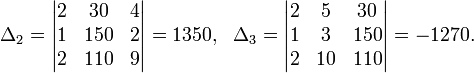
2. Метод Гаусса. Возможные завершения метода Гаусса:

Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Покажем, как методом Гаусса можно решить следующую систему:

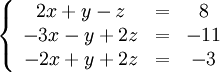
Обнулим коэффициенты при   во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на   и  , соответственно:

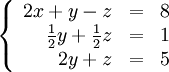
Теперь обнулим коэффициент при   в третьей строке, вычтя из неё вторую строку, умноженную на  :

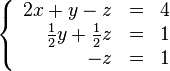
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

 из третьего;

 из второго, подставив полученное 

 из первого, подставив полученные   и  .

Таким образом исходная система решена.

В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.

2. Теорема Кронекера-Капелли:

Теорема Кронекера-Капелли — критерий совместности системы линейных алгебраических уравнений. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

2. Теорема о ранге матрицы и базисном миноре:

Определение: Ранг матрицы А - максимальный порядок неравного нулю минора (минор - определитель квадратной матрицы  ). Обозначается  .

Определение: Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие БМ, назвыаются базисными строками и столбцами.

Определение: Система столбцов   называется линейно зависимой   числа  , не все равные нулю и такие что: 

Теорема о базисном миноре:  Столбцы матрицы А, входящие в БМ, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через столбцы из БМ.