
14042,75 Долларов
Формулу вывожу следующим образом – строим геометрическую последовательность для каждого элемента аннуитета, рассчитывая наращение сложными процентами. Используя формулу суммы первых т членов геометрической последовательности получаем формулу для расчета искомого.
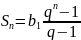
Где b1 первый элемент прогрессии, а q – знаменатель прогрессии.
Г-н N инвестировал 70 тыс. руб. в пенсионный контракт. На основе анализа таблиц смертности страховая компания предложила условия, согласно которым определенная сумма будет выплачиваться ежегодно в течение 20 лет исходя из ставки 15% годовых. Какую сумму будет получать ежегодно г-н N?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (70 тыс. рублей);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов начисления процентов (20 лет);
r – процентная ставка (15 %).
Преобразуем исходную формулу для нахождения решения задачи:
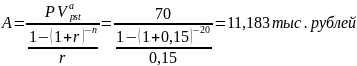
К моменту выхода на пенсию, т.е. через 8 лет, г-н N хочет иметь на счете 30 тыс. руб. Для этого он намерен делать ежегодный взнос в банк по схеме пренумерандо. Определить размер взноса, если банк предлагает 7% годовых.
Решение:
Имеется постоянный аннуитет пренумерандо с периодом один год и равным ему периодом начисления процентов.
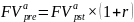 ,
где
,
где
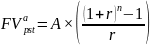
– будущая стоимость аннуитета пренумерандо (30 тыс. рублей);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов аннуитета, равное числу периодов начисления сложных процентов (8 лет);
r – сложная процентная ставка за период начисления (7 %).
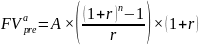 ,
,
Преобразуем исходную формулу для нахождения искомого:
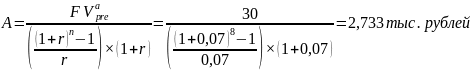
Стоит ли покупать за 5500 руб. ценную бумагу, генерирующую ежегодный доход в размере 1000 руб. в течение семи лет, если банк предлагает процентную ставку 8% годовых?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (искомое тыс. рублей);
A – размер аннуитета, сумма ежегодного платежа (1000 рублей);
n – число периодов начисления процентов (7 лет);
r – процентная ставка (8 %).
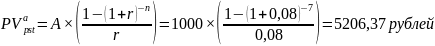
- это меньше цены бумаги (5500 рублей), следовательно приобретать ее не стоит.
Предприятие приобрело здание за 20 тыс. долл. на следующих условиях: а) 25% стоимости оплачиваются немедленно; б) оставшаяся часть погашается равными годовыми платежами в течение 10 лет с начислением 12% годовых на непогашенную часть кредита по схеме сложных процентов. Определите величину годового платежа.
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (75% от 20 тыс. долларов = 15 тыс. долларов);
A – размер аннуитета, сумма ежегодного платежа (искомое);
n – число периодов начисления процентов (10 лет);
r – процентная ставка (12 %).
Преобразуем исходную формулу для нахождения решения задачи:
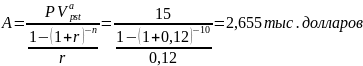
Г-н N хочет приобрести пенсионный контракт, по которому он мог бы получать ежегодно по 7000 руб. в течение оставшейся жизни. Страховая компания, используя таблицы смертности, оценила, что клиент сможет прожить 20 лет, и установила 6% годовых. Сколько нужно заплатить за контракт? А если установлено 8% годовых?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.
Базовая формула , где
– исходная (приведенная) стоимость аннуитета (искомое);
A – размер аннуитета, сумма ежегодного платежа (7000);
n – число периодов начисления процентов (20 лет);
r – процентная ставка (6 % ,8 %).
Стоимость контракта при ставке в 6 %:
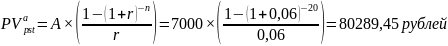
Стоимость контракта при ставке равной 8 % годовых:
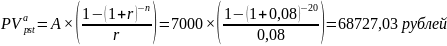
Раз в полгода делается взнос в банк по схеме пренумерандо в размере 500 долл. на условии 8% годовых, начисляемых каждые 6 месяцев. Какая сумма будет на счете через 5 лет? Как изменится эта сумма, если проценты будут начисляться раз в год?
Решение:
Имеется постоянный аннуитет постнумерандо с периодом один раз в полгода и полугодовым периодом начисления процентов.
, где
– будущая стоимость аннуитета пренумерандо (искомое);
A – размер аннуитета, сумма ежегодного платежа (1000);
n – период аннуитета (2);
m – число периодов начисления процентов, в году (2, 1);
l – срок аннуитета (5);
r – сложная процентная ставка за период начисления (8 %).
Получаем искомое:
