109,332 Тыс. Рублей.

13. Господин N инвестирует 40 тыс. руб. на 33 месяца под процентную ставку 26% годовых на условиях единовременного возврата основной суммы долга и начисленных сложных процентов. Проанализируйте, какую сумму предстоит вернуть банку при различных вариантах и схемах начисления процентов: а) полугодовое; б) квартальное.

Решение:

а) Наращения сложными процентами можно рассчитать, используя базовую формулу:

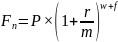, где

P – размер ссуды (40 тыс. рублей);

r – годовая ставка (26%);

m – количество начисления процентов в год (2;4)

w – число целых периодов начисления (5; 11);

f – дробная часть периода начисления (0,5; 0).

Получаем

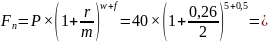78,431 тыс. рублей.

79,966 тыс. рублей.

б) Наращения по смешанной схеме можно рассчитать, используя базовую формулу:

78,488 Тыс. Рублей.

79,966 Тыс. Рублей.

14. Предлагается оформить вклад под следующие процентные ставки: 110% годовых или 22% за квартал, причем во обоих случаях используется смешанная схема начисления процентов. Какой вариант выгоднее, если срок хранения вклада составляет: а) 9 месяцев; б) один год? Финансовый год принять равным 360 дней (месяц - 30 дней).

Решение:

Наращение по смешанной схеме можно рассчитать, используя базовую формулу:

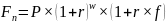, где

P – размер вклада (1);

r – годовая ставка (110%);

r⁴ – номинальная квартальная ставка (22%)

m – количество начисления процентов в год (1;4)

w – число целых периодов начисления (1, 3; 1; 4);

f – дробная часть периода начисления (-0,25, 0; 0; 0).

Получаем:

а)

110% годовых, 9 месяцев

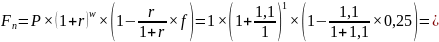1,825

22% квартальных, 9 месяцев

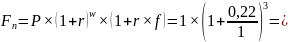1,816

Выгоднее вариант с годовым начислением процентов.

б)

110% годовых, 1 год

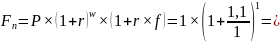2,1

22% квартальных, 1 год

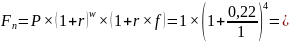2,22.

Выгоднее вариант с квартальным начислением процентов.

15. Некоторая сумма инвестируется под процентную ставку 30% годовых. Определите время, необходимое для увеличения первоначальной суммы: а) в 4 раза, б) в 2 раза при начислении в конце года сложных и простых процентов.

Решение:

Расчет наращения простыми процентами.

Базовая формула , где

R_n – возвращаемая сумма (4, 2);

P – исходная сумма (1);

n – число лет начисления процентов (искомое);

r – годовая процентная ставка (30 %).

Преобразуем исходную формулу для вычисления неизвестного (n).

Получаем .

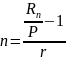Расчет наращения сложными процентами.

Базовая формула 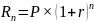, где

R_n – возвращаемая сумма (4, 2);

P – исходная сумма (1);

n – число лет начисления процентов (искомое);

r – годовая процентная ставка (30 %).

Преобразуем исходную формулу для вычисления неизвестного (n).

Получаем

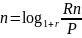
а) Простые проценты при 4-х кратном увеличении капитала

.

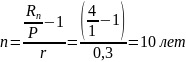Сложные проценты при 4-х кратном увеличении капитала

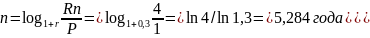
б) Простые проценты при 2-х кратном увеличении капитала

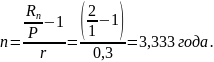
Сложные проценты при 4-х кратном увеличении капитала

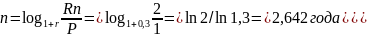
16. Вкладчик хотел бы за 7 лет утроить сумму, помещаемую в банк на депозит. Какова должна быть годовая номинальная процентная ставка при начислении сложных процентов: а) каждые полгода, б) каждый месяц.

Решение:

Расчет наращения сложными процентами при внутригодовом начислении процентов.

Базовая формула 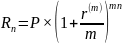, где

R_n – возвращаемая сумма (3);

P – исходная сумма (1);

m – число начислений сложных процентов в год (2, 12);

n – число лет начисления процентов (7 лет);

r^(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке r^m/m (искомое).

Преобразуем исходную формулу для вычисления неизвестного (r^(m)).

Получаем 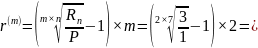0,1633 = 16,33 %

для полугодового начисления сложных процентов и

Получаем 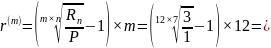0,158 = 15,80 %

для ежемесячного начисления сложных процентов.

17. В долг на 28 месяцев предоставлена сумма в 50 тыс. руб. с условием возврата 85 тыс. руб. Найдите эффективную ставку в этой финансовой сделке.

Решение:

Годовая эффективная ставка при однократном начислении сложных процентов за год обеспечивает результат как и номинальная процентная ставка. Расчет осуществляется по базовой формуле:

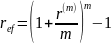
Номинальная процентная ставка - ставка, при которой за период 1/m года, проценты начисляются по ставке r^m/m.

Базовая формула , где

R_n – возвращаемая сумма (85 тыс. рублей);

P – исходная сумма (50 тыс. рублей);

m – число начислений сложных процентов (1);

n – число лет начисления процентов (28 месяцев/12 месяцев = 2,(3) года);

r^(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке r^m/m.

Получаем

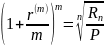, или ,

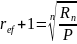Откуда вычисляем искомое значение

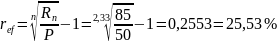
18. Из какого капитала можно получить 45 тыс. руб. через 6 лет наращением сложными процентами по процентной ставке 36%, если наращение осуществлять: а) ежегодно; б) ежеквартально?

Решение:

Расчет наращения сложными процентами при внутригодовом начислении процентов.

Базовая формула , где

R_n – возвращаемая сумма (45 тыс. рублей);

P – исходная сумма (искомое);

m – число начислений сложных процентов в год (1, 4);

n – число лет начисления процентов (6 лет);

r^(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке r^m/m (36 %).

Преобразуем исходную формулу для нахождения искомого:

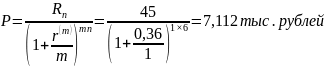
при годовом начислении.

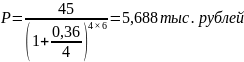
при ежеквартальном начислении.

19. Какую сумму необходимо поместить на банковский депозит, чтобы при непрерывном начислении процентов по ставке 25% получить 30 тыс. руб. через: а) 4 года; б) 9 лет?

Решение:

Расчет при непрерывном начислении процентов ведется по базовой формуле

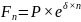, где

F_n – возвращаемая сумма (30 тыс. рублей);

P – исходная сумма (искомое);

e - математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. (e = 2,718281828)

n – число лет начисления процентов (4, 9 лет);

δ – непрерывная ставка (сила роста) (25 %).

Преобразуем исходную формулу для нахождения искомого:

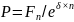
а)

б)

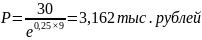
20. Банк выдает ссуду на 7 лет под сложную процентную ставку 36% годовых с начислением процентов каждые полгода. Какую непрерывную ставку должен установить банк, чтобы за 7 лет получить тот же доход?

Решение:

Расчет наращения сложными процентами при внутригодовом начислении процентов.

Базовая формула , где

R_n – возвращаемая сумма (искомое);

P – исходная сумма (1);

m – число начислений сложных процентов в год (2);

n – число лет начисления процентов (7 лет);

r^(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке r^m/m (36 %).

Определяем доход для начисления сложными процентами каждые полгода:

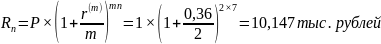
Расчет при непрерывном начислении процентов ведется по базовой формуле

, где

F_n – возвращаемая сумма (10,147 тыс. рублей);

P – исходная сумма (1);

e - математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. (e = 2,718281828)

n – число лет начисления процентов (7 лет);

δ – непрерывная ставка (искомое).

Преобразуем исходную формулу для нахождения искомого:

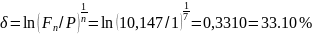
21. На вклад в 16 тыс. руб. начисляются непрерывные проценты. Определите наращенную сумму за 6 лет, если интенсивность наращения изменяется следующим образом: в первые два года равна 20%, следующие три года - 24% и в последний год - 26%. Какую постоянную силу роста необходимо взять, чтобы за 6 лет получить такую же наращенную сумму?

Решение:

Расчет при непрерывном начислении процентов ведется по базовой формуле

, где

F_n – возвращаемая сумма (рассчитываем);

P – исходная сумма (16 тыс. рублей);

e - математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. (e = 2,718281828)

n – число лет начисления процентов (2, 3, 1);

δ – непрерывная ставка (20 %,24 %,26 %).

Рассчитаем наращенную сумму за три периода начисления:

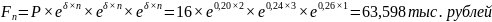
Преобразуем исходную формулу для нахождения решения задачи:

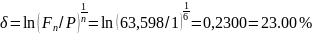
Более простое решение (без вычисления натурального логарифма)

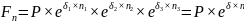
Путем преобразований получаем

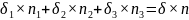
Искомое

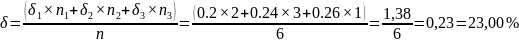
22. Господин N собирается поместить на некоторый срок свободные денежные средства либо под сложную процентную ставку 30% годовых с ежеквартальным начислением процентов, либо под простую процентную ставку 48% годовых. Выясните как выгоднее поступить при сроке: а) 3 года; б) 4 года.

Решение:

Расчет наращения сложными процентами при внутригодовом начислении процентов.

Базовая формула , где

R_n – возвращаемая сумма (искомое);

P – исходная сумма (1);

m – число начислений сложных процентов в год (4);

n – число лет начисления процентов (3, 4 года);

r^(m) – номинальная процентная ставка, такая ставка при которой за период 1/m года, проценты начисляются по ставке r^m/m (30 %).

Расчет наращения простыми процентами.

Базовая формула , где

R_n – возвращаемая сумма (искомое);

P – исходная сумма (1);

n – число лет начисления процентов (3, 4 года);

r – годовая процентная ставка (48 %).

а) ,

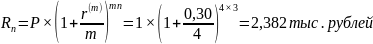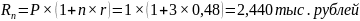
Выгоднее размещать денежные средства под простой процент.

б) ,

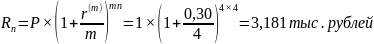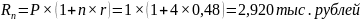
Выгоднее размещать денежные средства под сложный процент с ежеквартальным начислением процентов.

23. Банк принимает вклады до востребования под сложную процентную ставку 20% годовых при временной базе 365 дней. Какую простую годовую учетную ставку должен применить банк при учете векселя за 250 дней до срока его погашения, чтобы обеспечить себе такую же доходность, как и по вкладам до востребования? При учете используется временная база 360 дней.

Решение:

Расчет наращения сложными процентами.

Базовая формула 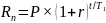, где

R_n – возвращаемая сумма (неизвестно);

P – исходная сумма (1);

t – число дней начислений сложных процентов (250);

T₁ – количество дней в году (365 дней);

r – годовая процентная ставка (20 %).

Базовая формула 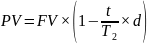, где

FV – возвращаемая сумма, сумма к погашению, номинальная стоимость (неизвестно);

PV – сумма покупки векселя банком (1);

t – количество дней до момента предъявления векселя (250 дней);

T₂ – количество дней в году (360 дней);

d – учетная ставка (искомое).

По условиям задачи доходность от обеих операций должна быть одинаковой, следовательно используем тождество, которое преобразуем для нахождения искомого значения.

.

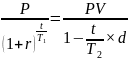Получаем путем преобразований

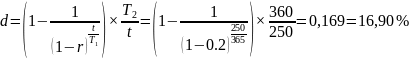
24. Вы заняли на четыре года 10 тыс. руб. под процентную ставку 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите величину годового платежа.

Решение:

Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.

Базовая формула 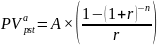, где

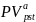– исходная (приведенная) стоимость аннуитета (10 тыс. рублей);

A – исходная (приведенная) стоимость (искомое);

n – число периодов начисления процентов (4 года);

r –процентная ставка (14 %).

Преобразуем исходную формулу для нахождения решения задачи:

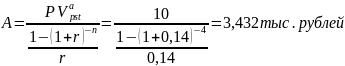
25. Вы заняли на пять лет 12 тыс. руб. под процентную ставку 12% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите какая часть основной суммы кредита будет погашена за первые два года.

Решение:

Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.

Базовая формула , где

– исходная (приведенная) стоимость аннуитета (12 тыс. рублей);

A – размер аннуитета, сумма ежегодного платежа (искомое);

n – число периодов начисления процентов (5 лет);

r – процентная ставка (12 %).

Преобразуем исходную формулу для нахождения решения задачи:

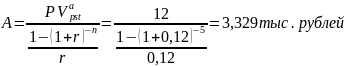
Год	Остаток основного долга на начало года, рублей	Величина годового платежа, рублей	В том числе, рублей		Остаток основного долга на конец года, рублей
			Проценты за год	Погашаемая часть долга
1	12000	3329	1440	1889	10111
2	10111	3329	1213	2116	7995
3	7995	3329	959	2370	5626
4	5626	3329	675	2654	2972
5	2972	3329	357	2972	0
∑		16 645	4645	12000

Остаток основного долга на начало первого года 12000 рублей.

Начисленные проценты за первый год 12000*0,12 = 1440 рублей.

Выплачена часть основного долга 3329-1440 = 1889 рублей.

Остаток основного долга на начало первого года 12000-1889 = 10111 рубль.

Начисленные проценты за второй год 10111*0,12 = 1213 рублей.

Выплачена часть основного долга 3329-1213 = 2116 рубля.

Итого за первые два года выплачено 1889+2116 = 4005 рубля

Или 33,4%

26. Вы заняли на пять лет 10 тыс. долл. под процентную ставку 8% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите общую сумму процентов к выплате.

Решение:

Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.

Базовая формула , где

– исходная (приведенная) стоимость аннуитета (10 тыс. долларов);

A – размер аннуитета, сумма ежегодного платежа (искомое);

n – число периодов начисления процентов (5 лет);

r – процентная ставка (8 %).

Преобразуем исходную формулу для нахождения ежемесячного платежа:

Общая сумма процентов равна

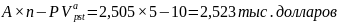
27. Предприниматель занял на шесть лет 45 тыс. руб. под 20%, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите величину процентов, которые будут уплачены предпринимателем в четвертом году.

Решение:

Имеется постоянный аннуитет постнумерандо с периодом один год и равным ему периодом начисления процентов.

Базовая формула , где

– исходная (приведенная) стоимость аннуитета (45 тыс. рублей);

A – размер аннуитета, сумма ежегодного платежа (искомое);

n – число периодов начисления процентов (6 лет);

r – процентная ставка (20 %).

Преобразуем исходную формулу для нахождения решения задачи:

Год	Остаток основного долга на начало года, рублей	Величина годового платежа, рублей	В том числе, рублей		Остаток основного долга на конец года, рублей
			Проценты за год	Погашаемая часть долга
1	45000	13532	9000	4532	40468
2	40468	13532	8094	5438	35030
3	35030	13532	7006	6526	28504
4	28504	13532	5701	7831	20672
5	20672	13533	4134	9399	11274
6	11274	13532	2258	11274	0
∑		81193	36189	45000

Остаток основного долга на начало первого года 45000 рублей.

Начисленные проценты за первый год 45000*0,2 = 9000 рублей.

Выплачена часть основного долга 13532-9000 = 4532 рубля.

Остаток основного долга на начало первого года 45000 - 4532 = 40468 рублей. И так далее.

Начисленные проценты за четвертый год – 5701 рубль.

28. На взносы в банк каждые полгода в течение 5 лет по 1000 долл. по схеме пренумерандо банк начисляет ежеквартально проценты по сложной процентной ставке 12% годовых. Какая сумма будет на счете в конце срока?

Решение:

Имеется постоянный аннуитет постнумерандо с периодом один раз в полгода и квартальным периодом начисления процентов.

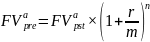, где

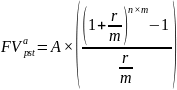
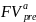– будущая стоимость аннуитета пренумерандо (искомое);

A – размер аннуитета, сумма ежегодного платежа (1000);

n – период аннуитета (2);

m – число периодов начисления процентов, в году (4);

l – срок аннуитета (5);

r – сложная процентная ставка за период начисления (12 %).

Получаем искомое: