Умножении целых чисел в дополнительных кодах

При представлении целых чисел в дополнительном коде знаковый разряд входит в число n разрядов. Следовательно, при умножении целых чисел (в отличие от дробных) в дополнительных кодах знаковый разряд участвует в умножении наряду со значащими. То есть умножение ведется на [Mт]_доп , а не на Мт.

1) Mн > 0,

Mт > 0.

Как отмечалось выше, в этом случае умножение выполняется по правилам умножения чисел в прямых кодах.

2) Мн>0,

Mт<0,

[Мт]_доп = 2ⁿ – Мт.

Т ак как сомножители имеют разные знаки, то произведение Мн∙Мт<0, сле­довательно, [Mн∙Мт]_доп=2²ⁿ - Mн∙Мт. Однако при умножении Мн∙[Мт]_доп получается Mн ∙(2ⁿ-Mт) =2ⁿ Mн - Mн∙Мт. Следовательно, погрешность в этом случае равна Δ = 2²ⁿ–Mн∙Мт–2ⁿ Mн+Mн∙Мт = 2²ⁿ–2ⁿ Mн = [–Мн]_доп∙2²ⁿ = [ [Мн]_доп]_доп∙2²ⁿ.

Пример: Mн = +110

Mт = -101

[Mн]_доп = 0.110

[Mт]_доп = 1.011

= [- Mн]_доп = 1.010

0.000

⁺ 0.110 = Mн∙b₄

0.110

0.011 0 ∙2^-1

⁺ 0.110 = Mн∙b₃

1.001 0 (возникло переполнение)

0.100 10 ∙2^-1 (коррекция)

0.010 010 ∙2^-1

⁺ 0.110 = Mн∙b₁

1.000 010 (возникло переполнение)

0.100 0010 ∙2^-1 (коррекция)

⁺ 1.010 (поправка)

1.110 0010 [MнMт]_доп

- 001 1110 MнMт

3) Мн<0,

Мт>0.

Здесь, как и при умножении дробных чисел, возможны два случая:

a) с вводом поправки в получаемое произведение

[Мн]_доп = 2ⁿ – Mн.

Как и ранее, требуется получить [Мн∙Мт]_доп= 2²ⁿ - Мн∙Мт. Получаем

(2ⁿ - Мн) ∙ Мт = 2ⁿ ∙ Мт - Мн∙Мт.

= 2²ⁿ - Мн∙Мт - 2ⁿ ∙ Мт + Мн∙Мт = 2ⁿ(2ⁿ - Мт) = [-Мт]_доп ∙ 2ⁿ ;

б) вариант без ввода поправки рассмотрим применительно к алгоритму умножения Г (как и ранее это справедливо и для других алгоритмов):

Mн∙Mт = A∙B = [A ∙ b₁ ∙ 2^-1 ]_доп + [A ∙ b₂ ∙ 2 ^-2]_доп+^- ... + [A ∙ b_n ∙ 2^-n]_доп=

=[A ∙ b₁ ∙ 2^-1 + A ∙ b₂ ∙ 2 ^–2 +^- ... + A ∙ b_n ∙ 2^-n]_доп=[Мн∙Мт]_доп.

Пример: Мн = -110 Мт = 101 [Мн]_доп = 1.010

[Мт]_доп = 0.101

b₁ ... b₄

0.0000000

⁺ 0.0000000 = [M_H ∙ b₁]_доп ∙ 2^-1

0.0000000

⁺ 1.1101000 = [M_H ∙ b₂]_доп ∙ 2^-2

1.1101000

⁺ 1.1111010 = [M_H ∙ b₄]_доп ∙ 2^-4

1.1100010

4) Mн < 0

Mт < 0

При этом сочетании знаков сомножителей в результате должно быть получено:

[Mн]_доп = 2ⁿ – Mн,

[Mт]_доп = 2ⁿ – Mт,

Mн ∙Mт = 2²ⁿ - [Mн Mт]_доп.

При умножении [Mн]_доп∙[Mн]_доп получается:

[Mн]_доп∙[Mн]_д =[Mн]_доп ( 2ⁿ - Mт ) = 2ⁿ [Mн]_доп -

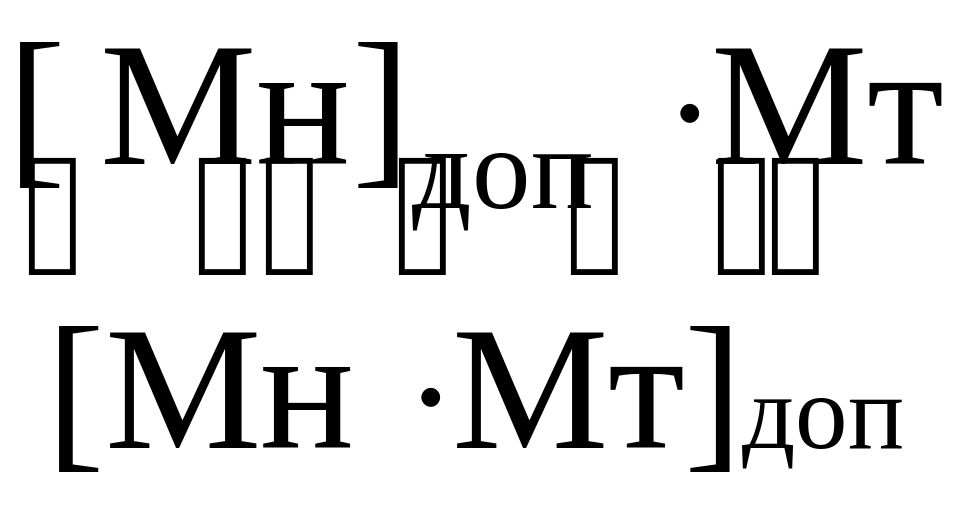
Пример: Мн = -110

Mт = -101

[Mн]_доп = 1.010

[Mт]_доп = 1. 011

b₁ ... b₄

= [[Mн]_доп]_доп= 0.110

При умножении используем алгоритм Г.

0.0000000

1.1010000 = [Mн∙b₁]_доп∙2^-1

1.1010000

1.1110100 = [Mн∙b₃] _доп∙2^-3

1.1000100

1.1111010 = [Mн∙b₄] _доп∙2^-4

1.0111110

0.110 (поправка)

0.0011110 Mн Mт