Симметричный магнитный вибратор. Конструкция, использование принципа перестановочной двойственности для определения поля в дальней зоне, а также проводимости излучения и входной проводимости.

Рассмотрим вибратор цилиндрической формы длины 2l и радиуса а, выполненный из идеального магнитного проводника и симметрично возбуждаемый в середине магнитодвижущей силой (МДС) , действующей в зазоре шириной b. Так как векторный потенциал магнитных токов подчиняется тому же уравнению, что и векторный потенциал электрических токов, и граничные условия в отношении магнитного поля в случае магнитного вибратора совпадают с граничными условиями в отношении электрического поля в случае электрического вибратора, то распределение магнитного тока в симметричном магнитном вибраторе, должно удовлетворять такому же интегральному уравнению (типа Г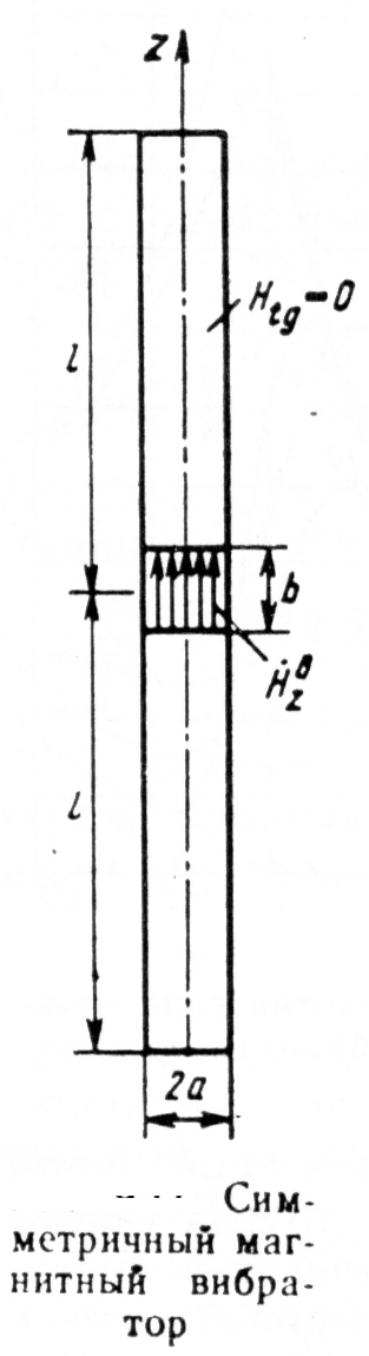 аллена или Поклингтона), как и для симметричного электрического вибратора. Следовательно, при а0 распределение магнитного тока по плечам симметричного магнитного вибратора в первом приближении является синусоидальным: , где - магнитный ток в пучности распределения. Следующие из принципа перестановочной двойственности замены , ЕН и z_C-1/Z_C дают возможность исходя из формулы: для поля электрического вибратора в дальней зоне сразу же получить дальнее электромагнитное поле симметричного магнитного вибратора:

; ; а также установить связи проводимости излучения и входной проводимости магнитного вибратора с сопротивлением излучения и входным сопротивлением электрического вибратора (имеются в виду вибраторы одинаковой формы и размеров): , . Отсюда следует, что входная проводимость магнитного вибратора имеет такую же частотную зависимость, как и входное сопротивление соответствующего электрического вибратора. В частности если полуволновый электрический вибратор в окрестности своей резонансной частоты эквивалентен (по схеме замещения) последовательному колебательному контуру с потерями, то магнитный полуволновый вибратор в окрестности резонансной частоты эквивалентен параллельному колебательному контуру.

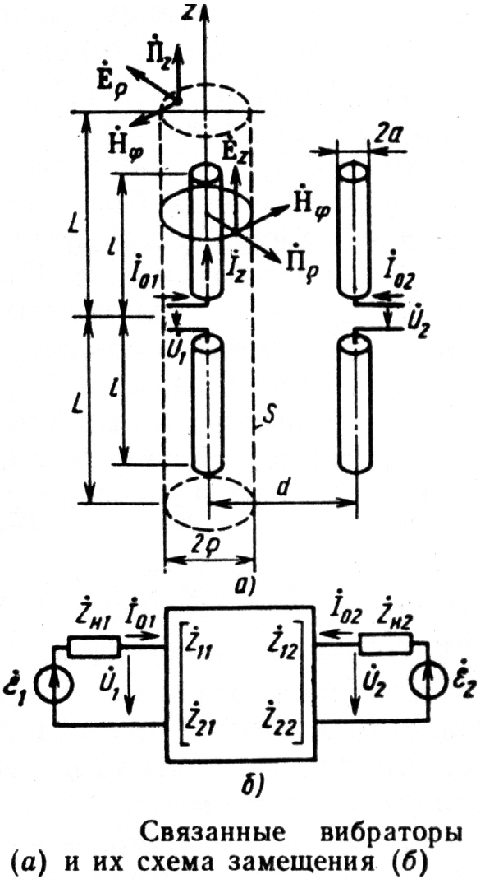
Связанные вибраторы. Метод наводимых ЭДС. Система связанных вибраторов. Схема замещения системы связанных вибраторов. Использование метода наводимых ЭДС для определения элементов матрицы сопротивлений.

Для увеличения КНД и получения одностороннего излучения используют антенную систему состоящую из нескольких вибраторов. Различают активные и пассивные вибраторы. Активные - подсоединенные непосредственно к вибратору, пассивные - не подсоединенные. Пусть имеется два параллельно расположенных вибратора.

Для определения токов и напряжений на входах вибратора систему можно

представить схемой замещения здесь z_Hi - комплексное сопротивление нагрузки; _i-ЭДС от генератора (в случае пассивного вибратора ₁=0), комплексные сопротивления z₁₁, z₂₂, …- комплексные сопротивления вибраторов. z₁₂=z₂₁ - взаимные сопротивления, учитывающие связь между вибраторами. Расстояние d обычно составляет от 0 до /4. При условии что d много больше а, а а<<l можно считать, что ток = ; где начало отсчета в центре вибратора, а l_1,2 - длины первого и второго вибраторов соответственно, токи и определяются из системы:

(*)

где и - внутренние сопротивления генераторов. Все числа в данной формуле являются комплексными. Для нахождения взаимных и собственных сопротивлений вибраторов применяется приближенный метод наводимых ЭДС.

Мощность на входе вибраторов можно представить в виде:

г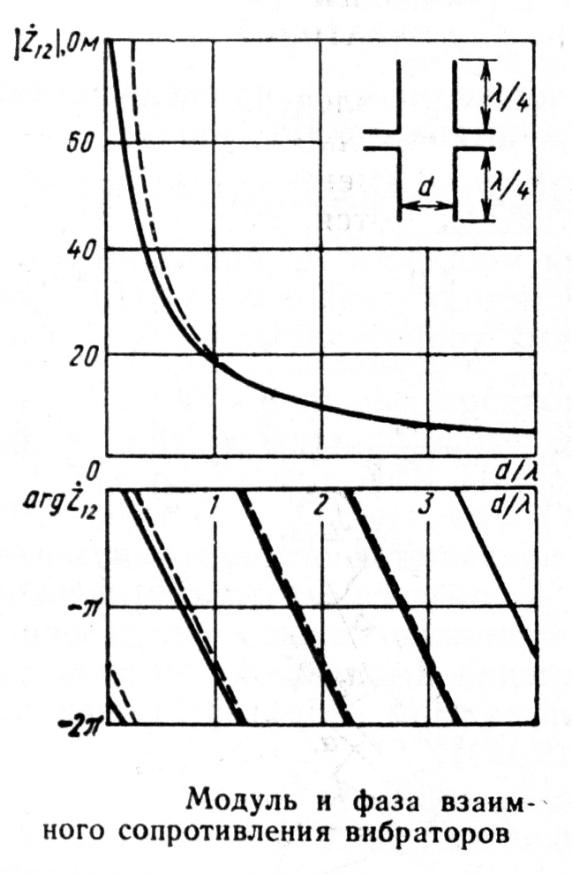 де Е_Z11 - составляющая порождаемая токами первого вибратора, Е_Z12 - составляющая порождаемая токами второго вибратора.

Из системы (*) можно записать, что

.

Сопоставляя мощности, приходим к соотношению:

Выражение для z₂₂ и z₂₁=z₁₂ получаются очевидной заменой индексов 12. Касательные составляющие Е_Z11 по существу представляют собой ЭДС, приходящееся на единицу длины вдоль боковой поверхности вибратора и порождаемые токами либо второго, либо первого вибратора, что и объясняет название метода наводимых ЭДС. Особенность: небольшие ошибки в задании распределения тока приводят к значительно меньшим ошибкам во взаимных и собственных сопротивлениях этим и объясняется широкое применение метода наводимых ЭДС в расчетах, он также положен в основу стандартных программ ЭВМ. В предельном случае при d=0 взаимное сопротивление превращается в собственное сопротивление полуволнового одновибратора и принимает собственное значение порядка 73,1 +j42,5 Ом, с увеличением расстояния d модуль z₁₂ плавно уменьшается. Фаза изменяется почти по линейному закону, соответствующего запаздыванию на 2 при увеличении d на одну длину волны .