15. Правила суммы и произведения.

Правило суммы гласит, что если А и В — несвязанные события, и существует n1 возможных исходов события A, и n2 возможных исходов события B, то возможное число исходов события «А или B» равно сумме n1 +n2.

Правило произведения утверждает, что если дана последовательность к событий с n1 возможными исходами первого, n2 — второго, и т. д., вплоть до nk возможных исходов последнего, то общее число исходов последовательности к событий равно произведению n1*n2…*nk. Правило суммы, по существу, — частный случай формулы включений и исключений. Действительно, если рассматривать А и В как множества исходов, то |А| = n₁, |В| =n₂; а поскольку события А и В не связаны друг с другом, то можно считать, что соответствующие множества не пересекаются. Тогда, по формуле включений и исключений, |A ∪ B| = |A| + |B|, т.е. множество AU В содержит n₁ +n₂ элементов. Это означает, что существует n₁ +n₂ возможных

исхода события «А или В». Правило произведения тоже можно сформулировать на языке теории множеств. Пусть A₁ обозначает множество n₁ исходов первого события, A₂ — множество n₂ исходов второго, и т. д. Тогда любую

последовательность k событий можно рассматривать как элемент декартова произведения A₁*A₂*…*A_k, чья мощность равна |A₁|*|A₂|…|A_k|.

16. Принцип включений и исключений. Принцип включений и исключений.

|А∪В| = |А| + |В|-|А⋂В|.

Доказательство. Как показано на рисунке множество A∪В состоит из подмножеств: А\В, А⋂В и В\А, которые не имеют общих элементов. Более того,

А = (А\В)∪(А⋂В) и В = (В\А)∪(А⋂В).

Введем обозначения:

|А\В|= m, |А⋂В| = n, |В\А|=р.

Тогда |А| =m+n, |B|=n+p и

|А∪В| = m+n+p =

= (m + n) + (n + р) — n =

= |А|+|В| + |А⋂В|.

17. Перестановки без повторений.

18. Сочетания без повторений. Предположим, что мы берем элементы x₁, x₂, ..., х_k из множества X мощности k. Каждый такой набор принято называть выборкой объема k из n элементов или, иначе, (n, k)-выборкой. Когда порядок следования элементов в выборке не имеет значения, то выборка называется неупорядоченной. Неупорядоченная (n, k)-выборка без повторяющихся элементов называется (n, k)-сочетанием без повторений. Число всех (n, k)-сочетаний без повторений обозначается символом C(n, k). Найдем его. Мы воспользуемся уже известным нам фактом: число всех (n, k)-размещений без повторений равно

Р(n, k)= . Дано (n, k)-сочетание без повторений, т. е. выбрано подмножество В ⊂ А, где |В| =k и |А| =n. Сколько из него можно получить разных (n, k)-размещений без повторений? Фактически, нам нужно подсчитать количество (k, k)-размещений без повторений. Это число мы знаем: P(k, k)= =k! Таким образом, на каждое (n, k)-сочетание без повторений приходится k! различных (n, k)-размещений без повторений. Стало быть, C(n, k)= =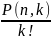

19. Сочетания с повторениями.

Предположим, что мы берем элементы x₁, x₂, ..., х_k из множества X мощности k. Каждый такой набор принято называть выборкой объема k из n элементов или, иначе, (n, k)-выборкой. Когда порядок следования элементов в выборке не имеет значения, то выборка называется неупорядоченной.

Неупорядоченная (n, k)-выборка с повторяющимися элементами называется (n, k)-сочетанием с повторениями.

Поскольку порядок в наших выборках значения не имеет, а повторы разрешены, мы можем сгруппировать вместе одинаковые элементы, разделив группы какими-нибудь метками.

Предположим, например, что мы сделали выборку, состоявшую из пяти букв, каждая из которых может быть одной из а, б и в. Выборку, состоящую из двух «а», одной «б» и двух «в», можно записать как аа|б|вв, а выборка из одной буквы «а» и четырех букв «в»

будет выглядеть так: а||вввв. Договоримся, что слева от первой метки либо стоят буквы «а», либо ничего, справа от второй метки — либо «в», либо ничего, а буквы «б», если они присутствуют в выборке, стоят между метками. Таким образом, можно считать, что

мы всегда смотрим на семь ячеек (пять букв и две метки), причем различные выборки будут отличаться ячейками, в которых стоят метки. Значит, число всех таких сочетаний с повторениями совпадает с количеством способов, которыми мы можем поместить две метки в семь ячеек. Осталось понять, что это количество есть не что иное, как число всех (7, 2)-сочетаний без повторений, т. е. равно С(7, 2). Действительно, первую метку можно поставить в любую из семи ячеек, а вторую — в любую из шести, поскольку одна ячейка уже занята. Это дает нам 7 * 6 возможностей. Заметим теперь, что поменяв расставленные метки местами, мы получим то же самое заполнение ячеек. Стало быть, 7*6 нужно разделить на 2. Итак, количество способов равно:

= = = =С(7,2) Возвращаясь к общему случаю (n, k)-сочетаний без повторений, заметим, что нам потребуется n -1 мет­

ка и k объектов. Таким образом, у нас будет (n - 1) + k ячеек для заполнения. Значит, число (n, k)-сочетаний без повторений совпадает с количеством способов размещения (n - 1) метки в (n+k - 1) ячейку. Итак, общее число (n, k)-сочетаний без повторений равно C(n+k-1, n-1)= =

20. Размещения без повторений. Предположим, что мы берем элементы x₁, x₂, ..., х_k из множества X мощности k. Каждый такой набор принято называть выборкой объема k из n элементов или, иначе, (n, k)-выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней задан. (n, k)-размещением без повторений называется упорядоченная (n, k)-выборка, элементам в которой повторяться запрещено; Для числа всех (n, k)-размещений без повторений зафиксировано специальное обозначение: P(n, k). Подсчитаем это число. На первое место выборки мы можем поставить любой из n элементов. Поскольку здесь нам не разрешены повторения, то для второго места мы можем выбрать любой из (n — 1) оставшихся элементов. На третье — из (n — 2) и так далее, вплоть до k-го места, куда можно написать любой из (n-k +1) элементов. Теперь для окончательного ответа нам нужно применить правило произведения. Имеем Р(n, k) = n(n - 1)(n - 2) • • • (n - k +1) Для сокращения записи проделаем легкие, хоть и не очевидные преобразования:

Р(n, k) = n(n - 1)(n - 2) • • • (n - k +1)= = n(n - 1)(n - 2) • • • (n - k +1) =

= =

Итак, число различных (n, k)-размещений без повторений равно P(n, k)=