13. Инъективные, сюръективные и биективные отображения. Примеры.

Функции — это частный случай бинарных отношений, на которые наложены дополнительные ограничения.

Функцией из множества А в множество В называется бинарное отношение, при котором каждый элемент множества А связан с единственным элементом множества В. Другими словами, для каждого a∈A существует ровно одна пара из отношения вида (а, b).

В графических терминах функция описывается таким графом, у которого из каждой вершины,изображающей элементы множества А, выходит ровно одна стрелка.

Например, на рисунке изображен граф, представляющий функцию из множества {а, b, с} в {1, 2}, состоящую из пар (а, 1), (b, 1) и (с, 2)

Пусть f : А —> В — функция. Мы будем называть ее инъективной или инъекцией, если f (a1) = f(a2) => ai=a2 для всех a1,a2 э А.

Это определение логически эквивалентно тому, что

а 1 не равно а2 => f( a 1) не равно (а2), т. е. у инъективнои функции нет повторяющихся значений. Иными словами, разные входные данные дают различные выходные данные.

Будем называть функцию f сюръективной или сюръекцией, если множество ее значений совпадает с областью значений. Это означает, что для каждого b э В найдется такой а э А, что b= f(a). Таким образом, каждый элемент области значений является образом какого-то элемента из области определения f.

Мы называем f биективной функцией или просто биекцией, если она как инъективна, так и сюръективна.

Например:

Данная функция не инъективна, поскольку значение 1 соответствует как а, так и b. Она не является и сюръекцией, ввиду того, что в элемент 2 ничего не переходит.

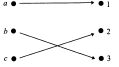
Данная функция инъективна, так как не имеет повторяющихся значений. Она же и сюръективна, поскольку множество ее значений совпадает со всей областью значений. Биективна, т.к. является и инъекцией и сюръекцией.

14. Обратные отображения. Критерий биективности отображения в терминах обратимого отображения. Напомним, что любая функция f : А —> В — бинарное отношение. Поэтому мы можем построить обратное отношение f^—1 . Если при этом мы снова получим функцию, то исходную функцию будем называть обратимой и писать f^—1 :B —> А для обозначения

обратной функции. Функция f состоит из пар вида (а, b), где b = f(a). Когда f обратима, обратная функция f ^–1 состоит из пар (b, а), где а = f^—1(b). Значит, обратимая функция должна удовлетворять условию: если f(а) = b, то f^—1(b) = а. Другими словами, обратная функция переворачивает действие исходной. Обратимы только биекции. Сейчас мы докажем критерий обратимости для общей функции f : А —> В. Теорема. Функция f обратима тогда и только тогда, когда она биективна.

Доказательство. Доказательство состоит из двух частей. Сначала мы докажем, что биективная функция обратима. Пусть f : А —> В — биекция. Как отношение, f можно определить с

помощью предикатов:

f= {(а,b): а∈А и f(а) = b}.

По определению обратного отношения имеем:

f^—1 = {(b,а): а∈A и f(а) = b}.

Поскольку f сюръективна, для любого элемента b ∈ В найдется такой а ∈ А, что f(а) = b. Кроме того, ввиду инъективности функции f такой элемент а определяется по b единственным образом. Следовательно, все пары отношения f^—1 обладают тем свойством, что каждый элемент множества В соответствует единственному

элементу множества А. А это, по определению, и означает, что f^—1 является функцией, как и утверждалось.

Теперь покажем, что обратимая функция обязана быть биективной. Предположим, что обратное отношение

f^—1 — функция. Тогда для любого b ∈ В существует единственный элемент а ∈ А, для которого (b, а) ∈f^—1 . Следовательно, (а, b) ∈ f, т.е. b = f(a). Этим доказана сюръективность f.

Для проверки инъективности функции f поступим следующим образом. Предположим, что f(a₁) = f(a₂)- Тогда обе пары: (f(a₁), a₁) и (f(a₂), a₂) — лежат в f^—1 . Так как f^—1 является функцией, имеет

место равенство: a₁ = а₂, так что f инъективна.

Таким образом, f является биекцией, как и утверждалось. Доказательство проведено полностью: обратимая функция биективна и, в обратную сторону, биективная функция обратима.