10. Булева алгебра множеств.

Булевой алгеброй называется непустое множество X с двумя бинарными операциями ⋂ (аналог конъюнкции), ∪ (аналог дизъюнкции), унарной операцией ¬ (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина).

Теорема 1. Для любых множеств X,Y,Z выпишем следующие свойства: 1. X⋂X=X и X∪X=X –св-во идемпатентности

2. X⋂X^C=∅ и X⋂X^C=U 3. X⋂Y=Y⋂X и X∪Y=Y∪X –св-во коммутативности 4. X⋂(Y⋂Z)=(X⋂Y)⋂Z и X∪(Y∪Z)=(X∪Y)∪Z-св-во

ассоциативности 5. (X⋂Y)^C=X^C∪Y^C и (X∪Y)^C=X^C⋂Y^C- законы де

Моргана

6.X⋂(Y∪Z)=(X⋂Y)∪(X⋂Z) и

X∪(Y⋂Z)=(X∪Y)⋂(X∪Z)-св-во дистрибутивности 7. (X^C)^C=X-закон двойного отрицания 8. X⋂∅=∅ и X∪∅=X X⋂U=X и X∪U=U

9. X⋂(X∪Y)=X и X∪(X⋂Y)=X-законы поглощения Док-во: (X⋂Y)^C содержится в X^C∪Y^C и X^C∪Y^C содержится в (X⋂Y)^C. Предположим, что x принадлежит (X⋂Y)^C, значит x не принадлежит X⋂Y. Пусть x не принадлежит X и не принадлежит Y. Иначе говоря: x принадлежит X^C и x принадлежит Y^C. Т.о., x принадлежит X^C∪Y^C. Значит, (X⋂Y)^C⊆X^C∪Y^C. Пусть x принадлежит X^C∪Y^C, т.о., x принадлежит X^C и х принадлежит Y^C. Значит, x не принадлежит X и не принадлежит Y.

11. Отношения. Представления отношений в виде орграфов и в виде логических матриц.

Бинарным отношением между множествами A и В называется подмножество R прямого произведения А х В. В том случае, когда А=В, мы говорим просто об отношении R на А. Имеется 2 удобных наглядных способа перечисления упорядоченных пар, принадлежащих данному отношению.

Первый способ основан на понятии «ориентированный граф», второй способ – использование логических матриц.

1)Пусть А и В – два конечных множества и R – бинарное отношение между ними. Мы изобразим элементы этих множеств точками на плоскости. Для каждой упорядоченной пары отношения R нарисуем стрелку, соединяющую точки, представляющие компоненты пары. Такой объект называется ориентированным графом или орграфом , точки же, изображающие элементы множеств, принято называть вершинами графа.

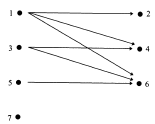
2)Второй способ задания бинарного отношения на конечных множествах основан на использовании логических матриц.

Предположим, что мы хотим определить бинарное отношение R между множествами А и В. Необходимо обозначить элементы множеств и выписать их в каком-нибудь порядке.

А={а₁,а₂,…,а_n} В= {b₁,b₂,…,b_m}

Для определения отношения R заполним таблицу M с n строками и m столбцами. Строки «перенумеруем» элементами множества А, а столбцы — элементами множества В в соответствии с порядком, в котором мы выписали элементы. Ячейку таблицы, стоящую на пересечении i-той строки и j-того столбца будем обозначать через М(i, j), а заполнять ее будем следующим образом:

М(i, j) = И, если (а_i, bj) принадлежит R,

M{i, j) = Л, если (а_i, b_j) не принадлежит R

Такого сорта таблицы называются n х m матрицами.

12. Свойства отношений: рефлексивность, симметричность, антисимметричность и транзитивность. Отношение R на множестве А рефлексивно, если для всех x∈А xRx;

симметрично, если xRyyRx для каждой пары x и y из А; кососимметрично, если (xRy и yRxx=y) для всех x и y из А; транзитивно, если (xRy и yRzxRz) для любой тройки элементов x,y,z∈A. В терминах упорядоченных пар эти свойства определяются следующим образом. Данное отношение R рефлексивно, если (x,x)∈R для любого возможного значения переменной x; симметрично, если из включения (x, y)∈R следует, что (y,x)∈R; кососимметрично, если из предположений : (x,y)∈R и x≠y вытекает, что (y,x)∉R; транзитивно, если включения (x,y)∈R и (y,z)∈R влекут (x,z)∈R. У ориентированного графа, изображающего рефлексивное отношение,каждая вершина снабжена петлей,т.е.стрелкой,начинающейся и заканчивающейся в одной и той же вершине. Орграф симметричного

отношения вместе с каждой стрелкой из вершины х в

вершину у имеет стрелку, направленную в обратную сторону: из у в X. Если отношение антисимметрично, то при наличии стрелки из вершины X в несовпадающую с ней вершину у, стрелка из у в х будет обязательно отсутствовать. И, наконец, орграф транзитивного отношения устроен так, что вместе со стрелками из вершины х в у и из у в z у него будет стрелка и из х в z.

Перечислим свойства матриц, задающих отношения. Прежде всего заметим, что матрица отношения на отдельном множестве А будет квадратной, т. е. количество ее строк будет равно количеству столбцов. Так вот, матрица М, задающая рефлексивное отношение, отличается от других тем, что каждый ее элемент, стоящий на главной диагонали (М(i, i)), равен И; матрица М симметричного отношения будет симметричной, т.е. M(i, j) = M(j, i); в матрице антисимметричного отношения выполнено условие:

(М(i, j) = И и i не равно j) => M(j, i) = Л.