4.Предикаты. Примеры предикатов.

Логика высказываний применяется к простым декларированным высказываниям, где базисные высказывания либо истинны, либо ложны. Утверждения, содержащие одну и более переменных, могут быть верными при некоторых значениях переменных и ложными при других.

Предикатом называется утверждение, содержащее переменные, принимающее значение истины или лжи в зависимости от значений переменных. Например, выражение «х — целое число, удовлетворяющее соотношению х = х²» является предикатом, поскольку оно истинно при x=0 или x=1 и ложно в любом другом случае.

Логические операции можно применять и к предикатам. В общем случае истинность составного предиката в конечном счете зависит от значений входящих в него переменных. Однако существуют логические операторы, называемые кванторами, применение которых к предикатам превращает последние в ложные или истинные высказывания.

5. Кванторы. Примеры высказываний, содержащих кванторы.

Выражения «для всех» и «найдется» («существует») называются кванторами и обозначаются, соответственно, ∀ и ∃. Включая в предикат кванторы, мы превращаем его в высказывание. Поэтому предикат с кванторами может быть истинным или ложным. Примеры: а)Сумма внутренних углов любого треугольника равна 180^о. P(x)={сумма внутренних углов треугольника x равна 180^о } (∀(x))(P(x)) б) Q(x)={целое число x удовлетворяющее соотношению x²=2} (∃(x))(Q(x))

6. Построение отрицания высказываний вида .

Отрицание высказываний (∀x(P(x)) и ∃x(P(x)) записывается в следующем виде: не(∀x(P(x))≡∃x(не P(x)) не(∃x(P(x))≡∀x(не P(x))

7. Методы доказательств: прямое доказательство, контрапозиция, метод доказательства от противного.

При доказательстве теорем применяется логическая аргументация. Доказательства в информатике — неотъемлемая часть проверки корректности алгоритмов. Необходимость доказательства возникает, когда нам нужно установить истинность высказывания вида (Р => Q). Существует несколько стандартных типов доказательств, включающих следующие:

1. Прямое рассуждение или прямое доказательство. Предполагаем, что высказывание Р истинно и показываем справедливость Q. Такой способ доказательства исключает ситуацию, когда Р истинно, а Q — ложно, поскольку именно в этом и только в этом случае импликация (Р => Q)

принимает ложное значение.

2. Обратное рассуждение или контрапозиция Предполагаем, что высказывание Q ложно и показываем ошибочность Р. То есть, фактически, прямым способом проверяем истинность импликации ((не Q) => (не Р)), что логически эквивалентно истинности исходного утверждения (Р => Q).

3. Метод «от противного». Предположив, что высказывание Р истинно, а Q ложно, используя аргументированное рассуждение, получаем противоречие. Этот способ опять-таки основан на том, что импликация (Р => Q) принимает ложное значение только тогда, когда Р истинно, а Q ложно.

8. Принцип математической индукции. Примеры доказательств утверждений с использованием принципа математической индукции. Проверка корректности алгоритма, содержащего циклы, нуждается в довольно мощном методе доказательства, который называется «математическая индукция». Принцип математической индукции

Пусть Р(n) — предикат, определенный для всех натуральных чисел n.

Предположим, что

1. Р(1) истинно и

2. ∀k ≥ 1 импликация (Р(k) =>Р{k+1)) верна.

Тогда Р(n) истинно при любом натуральном значении n. Пример: Методом математической индукции докажите, что 7ⁿ - 1 делится на 6 при любом натуральном показателе n.

Решение. Прежде всего напомним, что целое число а делится на целое число b тогда и только тогда, когда выполняется равенство а = mb при каком-то целом числе m. Кроме того, для наших рассуждений потребуется простое свойство делимости чисел, которое утверждает, что сумма делящихся на b чисел делится на b.

Пусть Р(n) обозначает предикат «7ⁿ -1 делится на 6».

При n = 1 имеем 7ⁿ - 1 = 7 - 1 = 6,

т.е. предикат Р(1) имеет истинное значение.

Предположим, что 7^k - 1 делится на 6 при каком-то натуральном k. Тогда:

7^k+1-1=7(7^k)-1=

=7(7^k-1)+7-1=7(7^k-1)+6

Так как 7^k-1 делится на 6, то по упомянутому свойству делимости сумма 7(7^k- 1) + 6 тоже делится на 6.

Итак, 7^k+1 - 1 делится на 6, так что при любом натуральном k импликация (Р(k) => Р(k + 1)) истинна.

Индуктивным рассуждением мы доказали истинность предиката Р(n) для всех натуральных n.

9. Множества. Дополнение, пересечение и объединение множеств. Множество — это совокупность объектов, называемых элементами множества. Например:

• {Гродно, Минск, Москва};

• {2, 3, 5, 7, 11};

• {сыр, яйцо, молоко, сметана}.

Порядок, в котором записываются элементы множества, значения не имеет.

∅ — пустое множество;

N = {1, 2, 3, ...} — множество натуральных чисел;

Z = {0, ±1, ±2, ±3, ...} — множество целых чисел;

Q ={ : p, q∈Z, q≠0} — множество рациональных чисел;

R = {все десятичные дроби} — множество вещественных чисел. Подмножеством множества S называется множество А, все элементы которого принадлежат S. Этот факт обозначается так: А ⊂ S. Два множества считаются равными, если они состоят из одних и тех же элементов. Объединением двух множеств А и В называется множество

А∪В = {х : х∈А или х∈В}

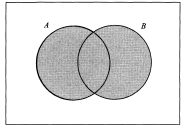
Пересечением двух множеств А и В называется множество

А⋂В = {х : x∈А и х∈В}.

Относительным дополнением множества В до множества А называется

А\В = {х : x∈А и x∉В}.

Дополнение множества A и B называется

Ā = {х : х∉А}