38. Бинарный сумматор

2-битный сумматор — это устройство, которое вычисляет сумму двузначных двоичных чисел, выдавая в качестве ответа трехзначное двоичное число.

На входе 2-битный сумматор получает два двузначных двоичных числа, а на выходе у него оказывается трехзначное число, равное сумме вводимых чисел. Иными словами, 2-битный сумматор складывает

числа в двоичной системе счисления.

Обозначим через а и b цифры первого вводимого в сумматор числа, а через с и d — цифры второго. Пусть е, f и g —цифры вычисляемой суммы.

Далее мы могли бы заполнить таблицы истинности цифр е, f и g, считая их булевыми функциями от вводимых цифр, упростить полученные выражения с

помощью карты Карно и начертить функциональную схему. Однако используем полубитный сумматор в качестве блока функциональной схемы. Схема, представленная на рисунке:

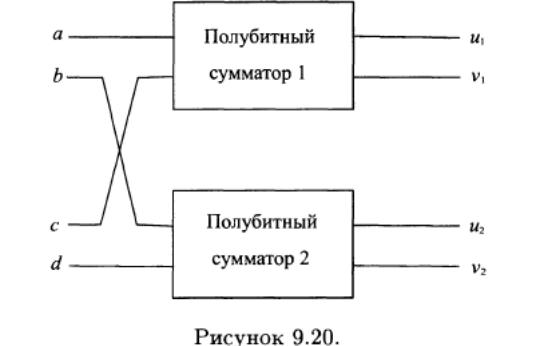
использует два полубитных сумматора для вычисления сумм: а+₂с и b +₂d.

Сумма по модулю 2 (переменная v₂) дает нам цифру g. Складывая разряд переноса u₂ с v₁ с помощью третьего полубитного сумматора, мы получаем двузначное число с цифрами u₃ и f . Наконец, последняя цифра суммы, е, может быть получена из u₁ и u₃ с

помощью функционального элемента ИЛИ.