54. Затухающие колебания.

Колебательный контур всегда обладает сопротивлением R, если подводящие провода и катушка индуктивности собраны не из сверхпроводящих материалов.

Проходя по такой цепи, ток выделяет джоулево тепло и расходует энергию, первоначально запасенную в колебательной системе.

К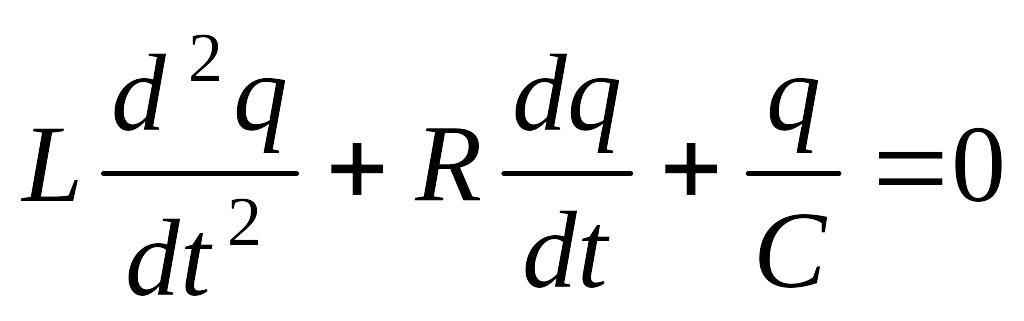 олебания в такой системе описываются уравнением, аналогичным незатухающим, но с добавлением слагаемого, описывающего потери энергии на сопротивлении RI:

По мере рассеяния энергии амплитуда колебаний затухает.

В этом случае решение уравнения естественно выбрать с амплитудой, убывающей со временем:

q(t) = eb-t a(t)

Разделим уравнение на L и введем обозначения:

2b º R/L,

w₀² º 1/СL,

b- коэффициент затухания.

У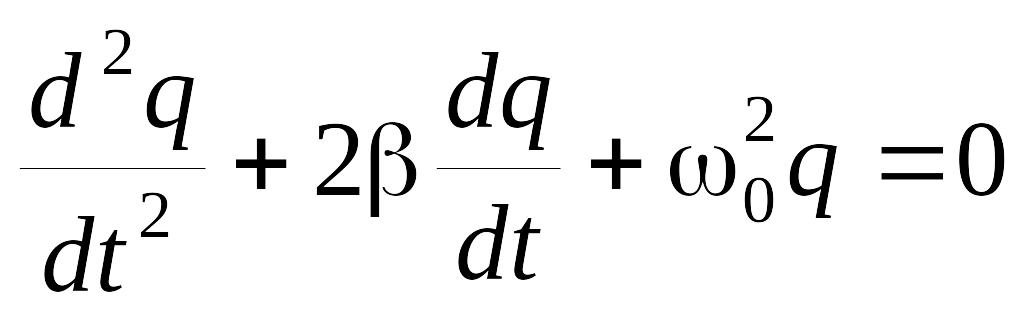 равнение преобразуется к виду

П одставив в него , придем к уравнению для переменной a(t):

Если величина w² = w₀² - b² > 0, то решение уравнения совпадает с ранее найденным для незатухающих колебаний:

a(t) = q₀ cos(wt + j ).

Величина заряда на обкладках конденсатора описывается зависимостью

q(t) = q₀ e-bt cos(wt + j ).

Функция q(t) не периодична в смысле q(t) = q(t + T), но она периодически обращается в нуль через равные промежутки времени Т/2 = p/w.

В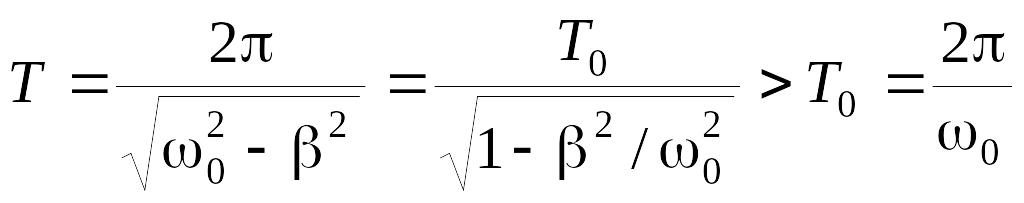 еличину Т = 2p/w называют периодом затухающих колебаний в смысле периодического обращения заряда в нуль

С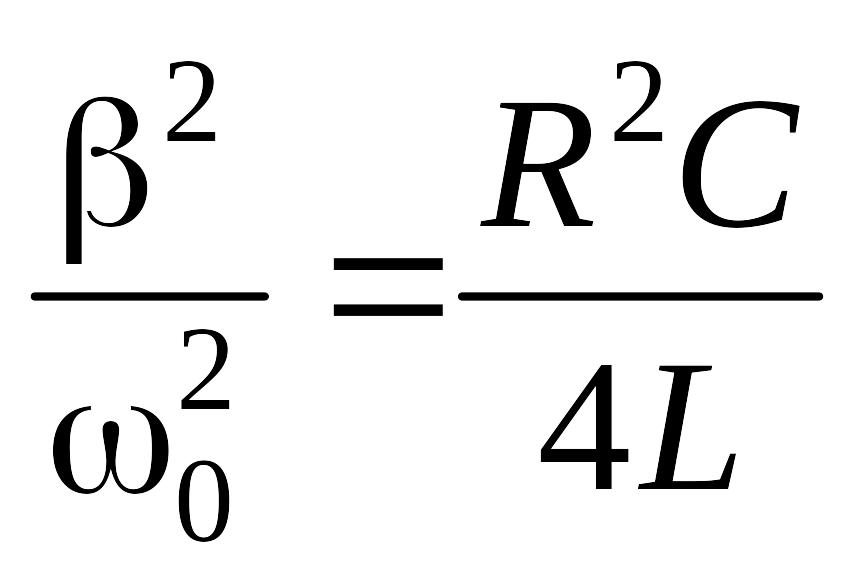 опротивление цепи понижает частоту колебаний в контуре и увеличивает период колебаний тем сильнее, чем больше отношение

Множитель q₀e^-bt называется амплитудой затухающих колебаний.

А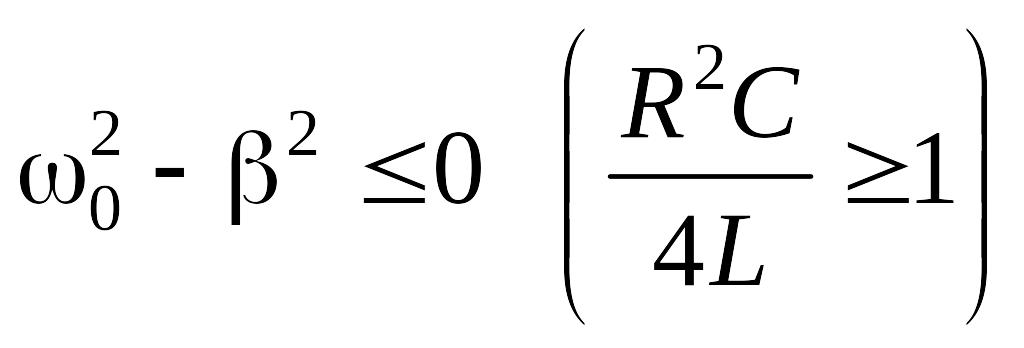 мплитуда колебаний при наличии сопротивления экспоненциально убывает со временем.

Если сопротивление цепи так велико, что , то процесс изменения заряда в цепи не будет колебательным,

а станет апериодическим.

55. Логарифмический декремент затухания. Добротность.

Затухание колебаний характеризуется логарифмическим декрементом затухания l.

О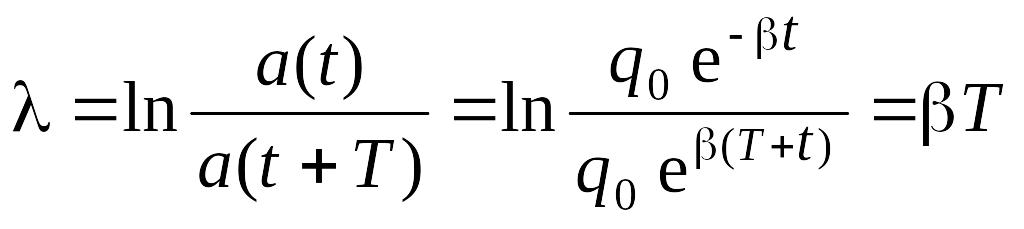 н равен натуральному логарифму отношения амплитуд колебаний, отличающихся по времени измерения на период

Здесь a(t) - амплитуда колебаний изучаемой величины, например q, I, U и пр.

В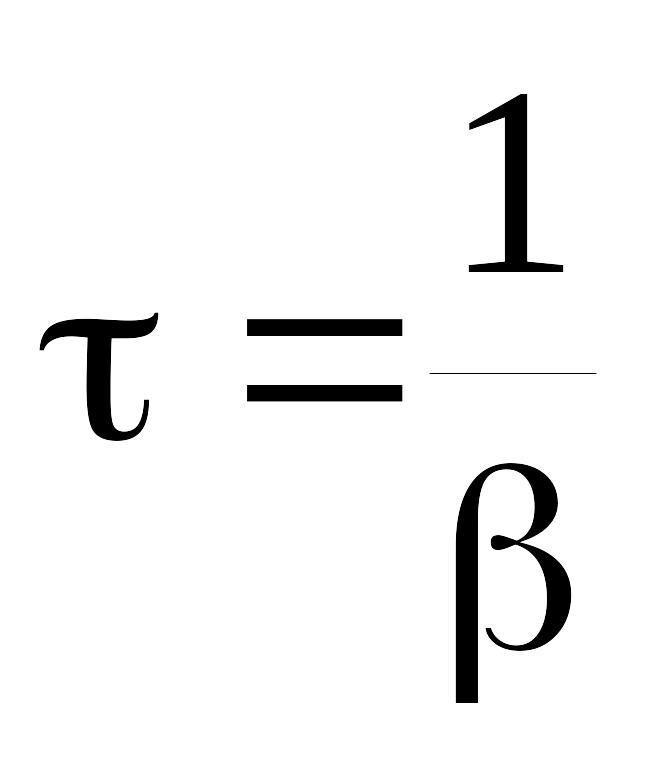 ремя t, по истечении которого амплитуда колебаний убывает в е раз, называется временем затухания:

З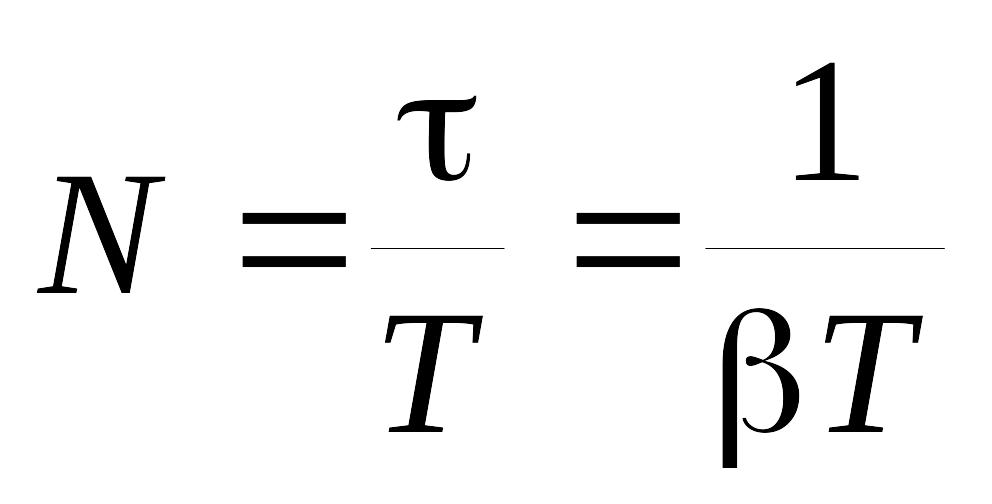 а время t система совершит N полных колебаний, где

Т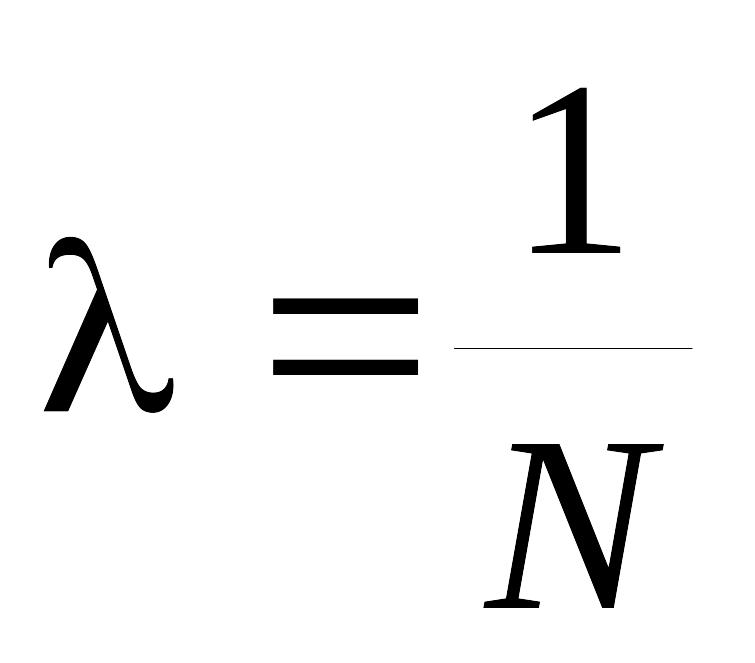 аким образом, логарифмический декремент затухания связан с числом колебаний N, приводящим к уменьшению амплитуды в е раз соотношением

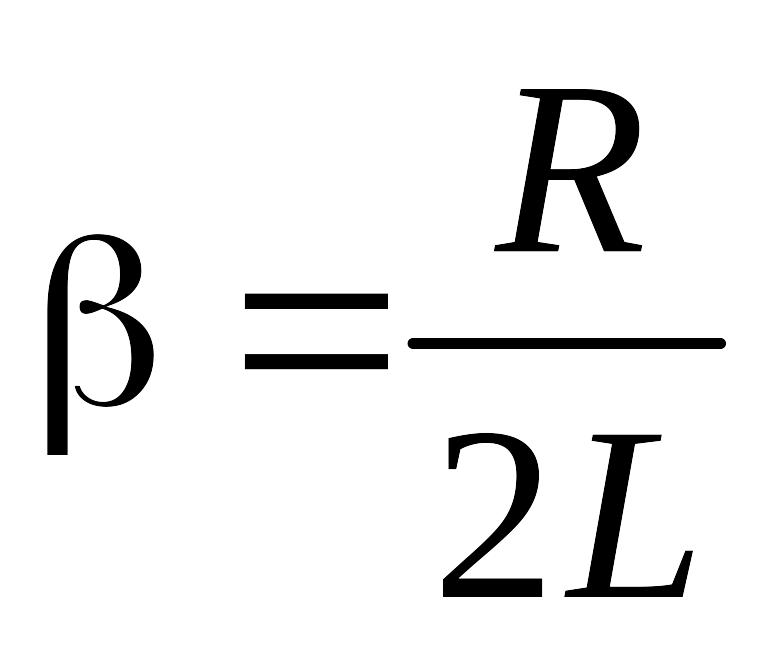
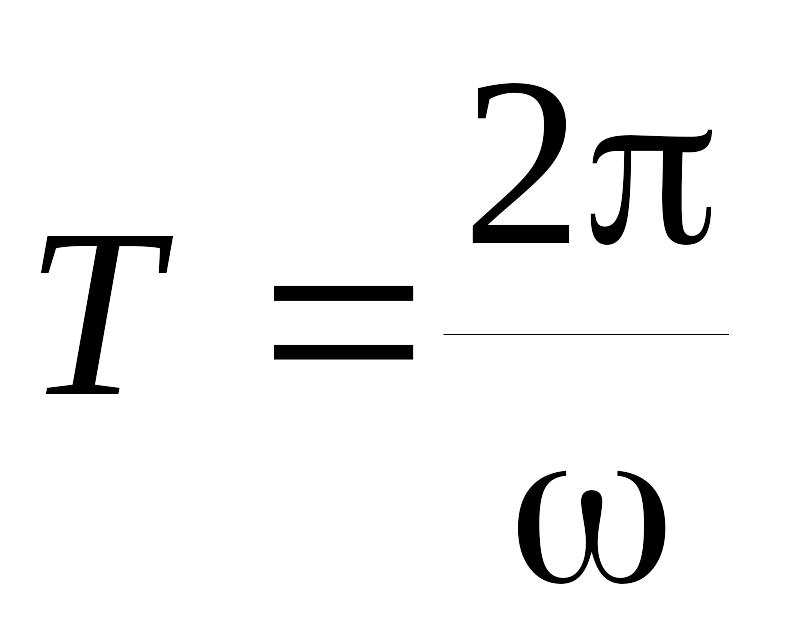
Подставляя в выражение для l значения и , получаем

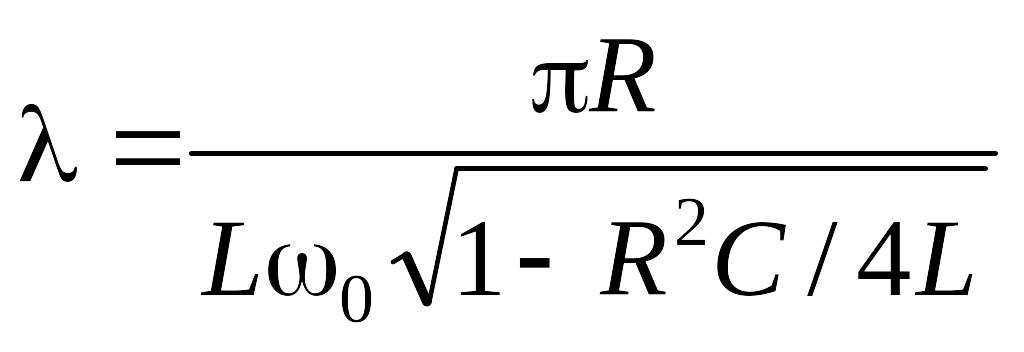
Если затухание в системе невелико , то .

В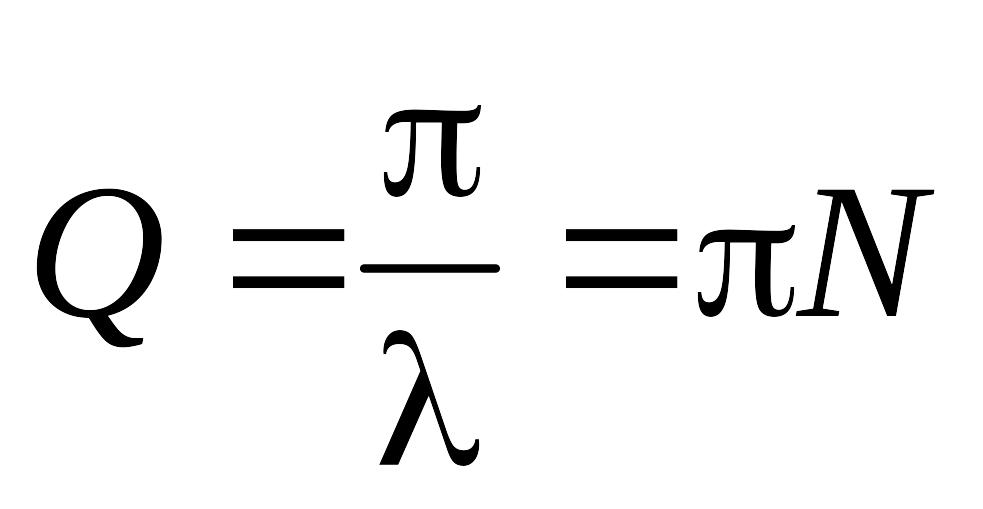 ажнейшей характеристикой колебательного контура является добротность Q, величина, обратно пропорциональная логарифмическому декременту:

Ч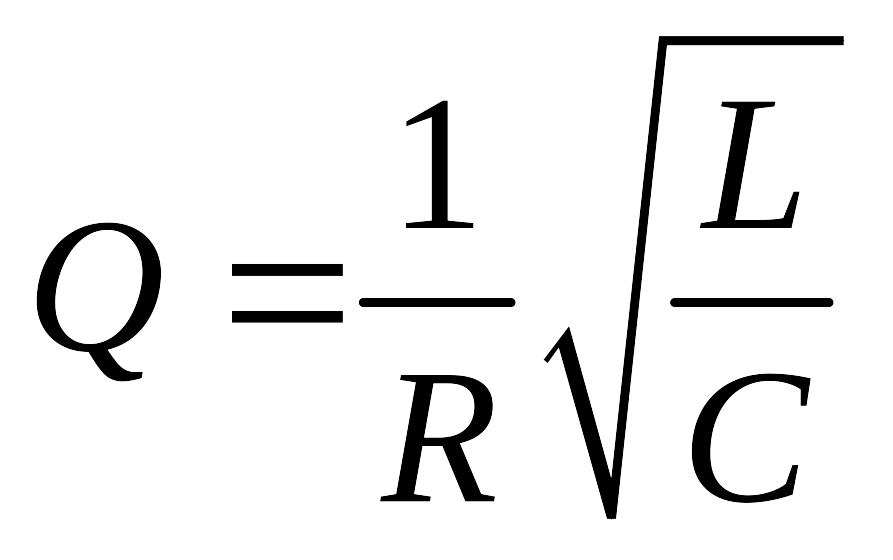 ем выше добротность, тем большее число колебаний успеет совершить система, прежде чем амплитуда колебаний уменьшится в е (2,71826) раз. При слабом затухании

Добротность тем выше, чем меньше относительные потери энергии в контуре за период.