Аппроксимация ортогональными многочленами.

Рассмотрим задачу аппроксимации функции F(x), заданной на интервале [a, b] , т.н. обобщенным многочленом

P_m(x)= ( 17 )

где _i(x) - система линейно независимых и ортогональных на [a, b] с весом (x) функций:

( _i , _k )= . ( 18 )

Минимизация

R(a₀ , a₁ , a₂ , . . ., a_m )= ( 19 )

на классе обобщенных многочленов приводит к системе :

Возьмем систему тригонометрических функций:

1 , Cos(x) , Sin(x) , Cos(2x) , Sin(2x) , . . . , Cos(mx) , Sin(mx) ,

ортогональных на интервале [0, 2] :

;

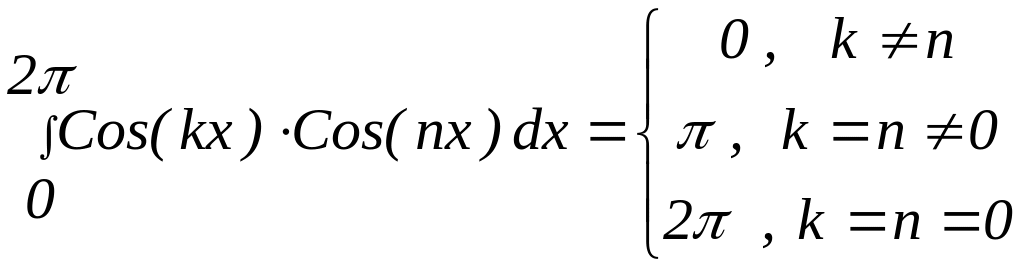
C учетом (20) при (x)=1 получаем:

P_m(x)= , ( 21 )

где

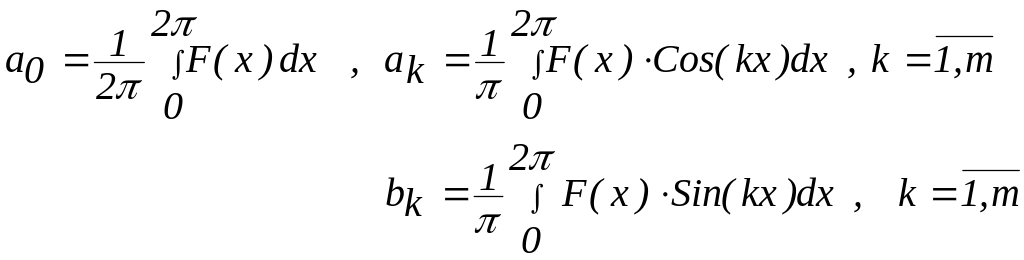( 22 )

Таким образом, мы получили аппроксимацию тригонометрическим многочленом, или отрезком ряда Фурье.

Полиномы Лежандра (частный случай т.н. сферических функций) определяются в форме

L_n(x)= , ( 23 )

откуда для аппроксимации

P_m(x)= ( 24 )

имеем

. (24a)

Полиномы Чебышева первого рода определяются в виде

T_n(x)=Cos( n  arcCos(x) ) , ( 25 )

откуда

T₀(x)=1 , T₁(x)= x , T₂(x)= 2x² -1 , T₃(x)= 4x³-3x ,

T₄(x)=8x⁴-8x²+1 , T₅(x)=16x⁵-20x³+5x , ...

Заметим, что при n>1 для вычисления значений полиномов Чебышева первого рода можно воспользоваться удобным рекуррентным соотношением :

T_n(x) = 2x T_n-1(x) - T_n-2(x) . (25a)

Для этих полиномов обнаруживается ортогональность на интервале [ -1 , 1 ] c весом :

, (25б)

откуда для аппроксимации

P_m(x)= ( 26 )

имеем

(26а)

Если взять m=4 и F(x)=x, то после нахождения коэффициентов

a₀=2/, a₂=-1/3 , a₄= - 4 /15 , a­₁=a₃=0

получаем

P₄(x)= .

При аппроксимации на интервале [0 , ) прибегают к использованию полиномов Лагерра, в простейшем случае задаваемых в виде

, (27)

(в частности,

L₀(x)=1 , L₁(x)= x-1 , L₂(x)=x²-4x+2 ,

L₃(x)=x³-9x²+18x-6 , L₄(x)= x⁴-16x³+72x²-96x+24 ,

L₅(x)= x⁵-25x⁴+200x³-600x²+600x-120 , ...

и рекуррентное соотношение

L_n+1(x)=(x-2 n-1) L_n(x) - n² L_n-1(x) , n  1 )

ортогональных с весом e^-x :

и при аппроксимации

P_m(x)=

дающих

(27а)

При аппроксимации на всей действительной оси можно воспользоваться полиномами Эрмита (функциями параболического цилиндра)

, ( 28 )

первые из которых равны

H₀(x)=1 , H₁(x)= 2x , H₂(x)= 4x²-2 , H₃(x)=8x³-12x ,

H₄(x)= 16x⁴- 48x²+12 , H₅(x)= 32x⁵- 160x³+120x ,

связанных рекуррентным соотношением

H_n+1(x)= 2x H_n(x) +2 n L_n-1(x) , n  1 ,

ортогональных на (-  ,  ) с весом

и при аппроксимации

P_m(x)=

дающих

(28а)

Иногда вместо H_n(x) используют полиномы

H^*_n(x)= (29)

с другой нормировкой и единичным коэффициентом при старшей степени.

Аппроксимация полиномами Эрмита наиболее точна в окрестности нуля (здесь весовая функция минимальна).