Среднеквадратическая аппроксимация и метод наименьших квадратов.

Пусть имеется таблица N значений аргумента x_i и соответствующих значений функции F_i

Поставим задачу поиска функции из класса алгебраических многочленов m -го порядка

F(x)= a₀+a₁x+a₂x²+ . . . + a_mx^m ( 1 )

такой, что сумма квадратов отклонений ее от табличной функции

( 2 )

является минимальной.

Очевидно, что частные производные функции R при оптимальном выборе неизвестных коэффициентов многочлена должны обращаться в нуль, откуда возникает система уравнений

, ( 3 )

или

.

Если обозначить через

, ( 4 )

то из (3) с учетом (1) возникает система линейных алгебраических уравнений с симметрической матрицей коэффициентов, определитель которой отличен от нуля (если значения x_i не равны константе), что гарантирует существование и единственность ее решения (для решения можно воспользоваться любым из известных методов, в частности, методом квадратных корней)

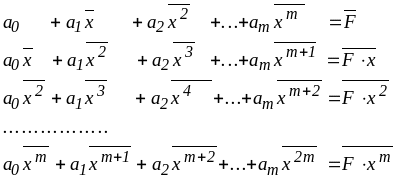( 5 )

Как частный случай (1) можно получить аппроксимацию линейной функцией

F(x)= a+b x ( 6 )

с коэффициентами

, (6a)

аппроксимацию квадратичной функцией

F(x)=a+bx+cx² ( 7 )

с коэффициентами, получаемыми решением системы

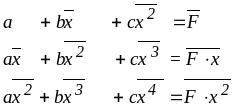(7a)

или какую-либо другую.

MatLab достаточно задать векторы X, F , степень полинома m:

for k=1: m+1

T(:,k)=X'.^(k-1);

end

R=T'*T;

B=T'*F';

A=R\B

при больших степенях полинома и неудачном выборе масштаб для значений х может возникнуть “потеря значности” (обращение коэффициентов при высших степенях в нуль) или “прерывание по переполнению разрядной сетки”. Это чревато большой погрешностью. Поэтому к степеням выше 5-6 обычно не прибегают

Среднеквадратическая аппроксимация функций на интервале.

Аппроксимация алгебраическими многочленами.

Пусть известна некоторая функция F(x), заданная на интервале [a, b] каким-то трудоемким для массовых вычислений выражением. Попытаемся заменить ее более простой функцией, например, алгебраическим многочленом

P_m(x)= a₀+a₁x+a₂x²+ . . . + a_mx^m . ( 13 )

Потребуем минимума

R(a₀ , a₁ , a₂ , . . ., a_m )= ( 14 )

среди всех алгебраических многочленов степени не выше m.

Приравняв нулю частные производные R по a_i, получаем линейную систему:

Например, если взять a= -1 , b=1 , то при m=4 имеем систему [20]: