Метод квадратных корней.

Идея методов итераций (последовательных приближений) состоит в преобразовании системы уравнений AX=B к системе

Практически то же самое что и метод Краута на пару со схемой Холецкого, но только этот метод для симметрических матриц, таких у которых Aij=Aji.

Любую симметрическую матрицу можно разложить на такое произведение:

A=R*Rt, где Rt-транспонированная матрица (эта такая матрица, у который на месте столбцов стоят строки и наоборот, у симметрических матриц транспонированная им равняется).

А вот чтобы найти второй множитель R, надо посчитать ее элементы опять таки по формулам:

rii=корень(aii-сумма(rki^2)), где k=1,...,i-1, i=1...n

rij=(1/rii)* (aij - сумма(rki*rkj)), где k=1,...,i-1, j=i+1...n

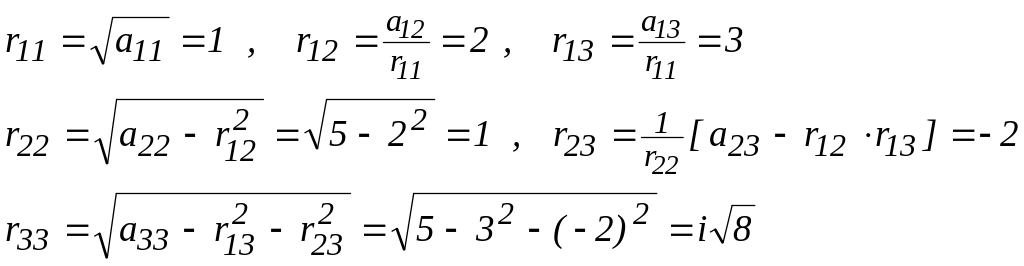
Нашли матрицу R, теперь также как и в методе Краута заменяем исходное уравнение на два других с использованием найденной треугольной матрицы R на RtY=B, RX=Y

И снова по формулам ищем Y:

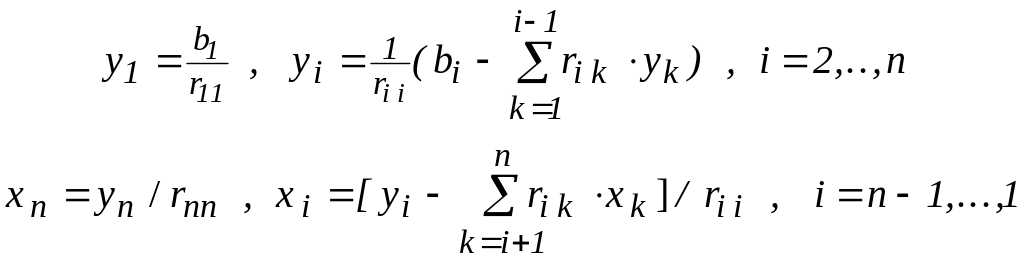
Метод простой итерации и сходимость итераций.

При больших значениях n прямые методы лишь формально являются точными, в реальности давая весьма высокую вычислительную погрешность.

Идея методов итераций (последовательных приближений) состоит в преобразовании системы уравнений AX=B к системе

Тот же принцем, в простой итерации. Мы берем какую-то начальную точку приближения и от нее двигаемся в цикле все ближе к значению с нужной нам точностью.

Сначала нам понятное дело надо заменить уравнения в системе и привести их к виду X =  X +  ну короче выразить из каждого уравнения по иксу. Чтобы ваш цикл не расколбасило, нужно соблюсти условие ||a||<1, т.е. норма матрицы должна быть меньше 1. Чтобы так было, когда будите выражать иксы из уравнений, нужно в каждом уравнении найти наибольший коэффициент и выражать тот икс, который при этом максимальном коэффициенте.

Метод Зейделя.

Перепишем процесс простой итерации (17) в развернутом виде

. ( 17a)

Метод Зейделя отличается тем, что на очередной итерации берут не оценки предыдущей итерации, а самые последние из полученных:

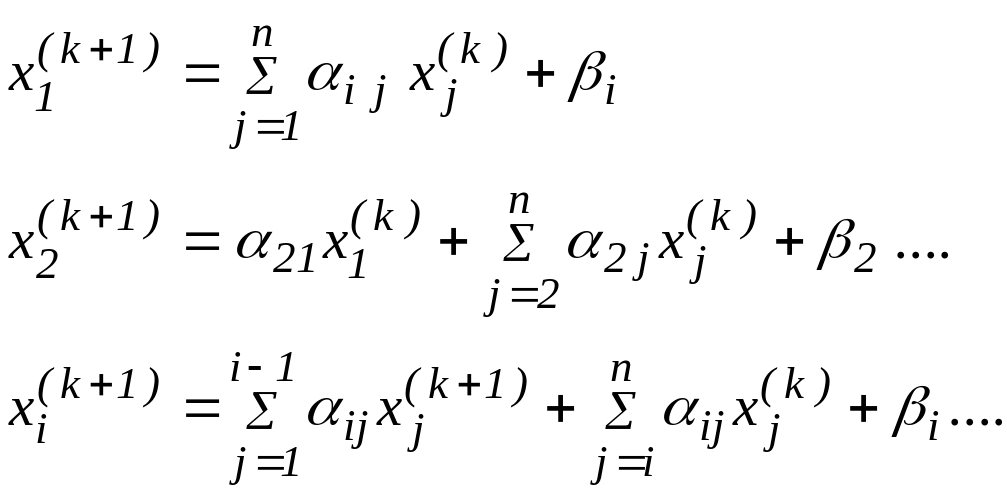( 19)

Как правило, использование метода Зейделя дает ускорение сходимости приближений к истинному решению. Условия сходимости те же, что и для метода простой итерации.

Очевидно, что при решении систем небольшой размерности использование итерационных методов едва ли разумно; при большой размерности они дают достаточно точное решение при любом начальном приближении, т.е. устойчивы к возникновению вычислительных ошибок, чем не могут похвастаться прямые методы.

Метод прогонки для систем с трехдиагональной матрицей.

Этот метод для трехдиагональных матриц, это когда заполнена главная диагональ и две по бокам, остальные элементы нули. Предполагают, что xk=Pk*Xk+1 + Qk, k+1 это коэффициент икса, k=0...n-1

Эту хреновину подставляют в уравнению вместо икса, делают преобразования с раскрытием скобок и прочее и в итоге получается ( a_k P_k-1 +b_k) x_k + c_kx_k+1 = d_k - a_k Q _k-1 , k=2, ... , n-1 , Потом через какую-то магическую щель вытаскивают формулы для нахождения этих коэффициентов P и Q, и для иксов. Метод состоит из двух ходов, сначала в прямом ходе нам нужно найти коэффициенты, а потом в обратном ходе сами иксы и все по формулам: