Решение систем нелинейных уравнений.
системы уравнений можно решать теми же методами, что и обычные уравнения.
Можно применить и метод простой итераций, заменив каждое из уравнений системы на их эквиваленты ну и все как обычно, только с двумя уравнениями одновременно.
Еще есть Метод Зейделя, он именно для систем и является модифицированным методом простых итераций. Его отличие в том, что у нас же система и мы ищем сразу несколько иксов, так вот для подсчета каждого икса мы используем предыдущий вычисленный (все в рамках одной итерации).
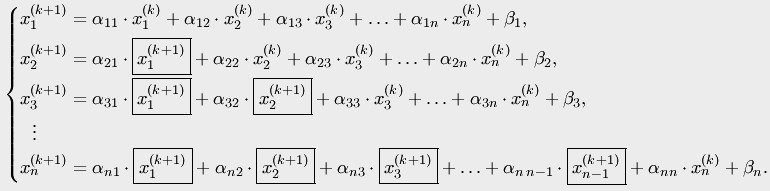Важным условием
сходимости этого метода является то,
что ||A||<1, т.е. норма матрицы должна быть
меньше 1 (проще говоря, все коэффициенты
в уравнении должны быть в сумме меньше
1). Если это условие не выполняется, то
надо попробовать попереставлять
уравнения, чтобы достигнуть выполнение
этого условия.
Также можно использовать и метод Ньютона. Для системы n уравнений сделаем матрицу W(X) в которую запишем частные производные, и теперь мы можем в цикле искать иксы по формуле:
Xk+1=Xk - W^-1(Xk)*F (Xk)
ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
Метод Гаусса (схема полного исключения, сведение к треугольной матрице, проблема погрешности, схема главных элементов).
Метод Гаусса.
Схема единственного деления .Делим первое уравнение на Первый его коэффициент А11, если он больше нуля, а затем исключаем переменную из остальных уравнений, для этого надо из каждого уравнения вычесть первое предварительно его умножив на коэффициент при той переменной, которую мы убираем. И так мы исключаем остальные переменные. Потом делаем обратный ход и начиная с конца с помощью подстановки находим иксы. В общем смотрите в видео, там все намного яснее.
Схема полного исключения. Тут то же самое что и в предыдущем, только переменные исключаются не только из последующих уравнений, но и из предыдущих.
Схема главных элементов. Здесь мы делим уравнение не на первый его ненулевой коэффициент, а на самый большой по модулю. И также исключаем соответствующую этому элементу переменную из следующих уравнений
Разложение матрицы в произведение треугольных и метод Краута.
Схема Холецкого заключается в том, что любую квадратную матрицу размерности n (т.е. матрицу nxn) можно разложить на произведение двух треугольные матрицы. У одной по правую сторону от главной диагонали будут нули, а у другой главная диагональ будет вся в единицах и по левую сторону от диагонали будут нули.
A=B*C
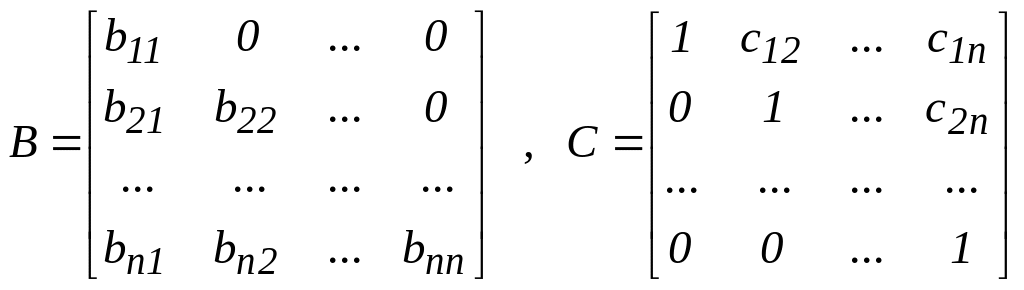
элементы этих матриц находятся по следующим формулам:
Элементы матрицы В (той, где нули с правой стороны):
b11=a11, bij=aij - сумма(bik*ckj), где k=1,...,j-1, при i>=j>1
Элементы матрицы С, где диагональ с единицами:
с1j=a1j/b11, cij=(1/bii)*(aij - сумма(bik*ckj)), где k=1,...,i-1, при 1<i<j
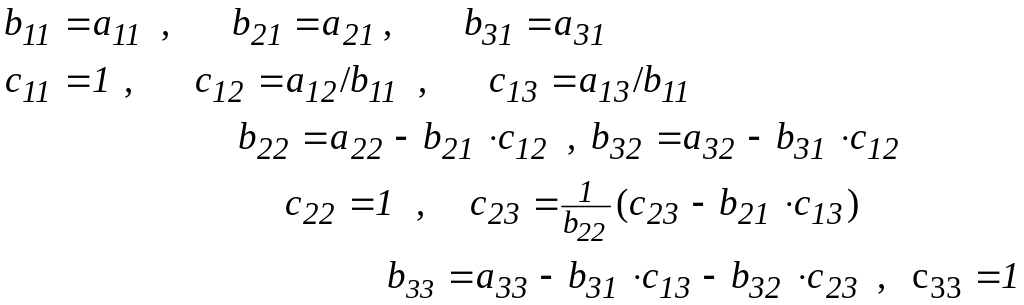
Вот мы разложили матрицу на две, зачем? Чтобы воспользоваться методом Краута. Он заключается в том, что исходное уравнение AХ=D, мы теперь можем заменить на два других, т.к. матрицу A мы разложили на B и C, то получим два уравнения BY=D, CX=Y
Сначала понятное дело находим игрики, а потом уже иксы. Находятся и те, и другие тоже по формулам:
