Простейшие методы решения задачи Коши.

Возьмем уравнение y’(x)=f(x,y) с начальным условием y(x₀) = y₀ и попытаемся найти y(x) для x = x₀+n h , n=1,2, ...

Взяв разложение в ряд Тейлора и ограничившись двумя членами разложения, имеем

y(x+h)=y(x_n)+h y’(x_n)+O(h²).

Введя для краткости записи обозначения x_n = x₀+n h , y_n= y(x_n), получаем отсюда

y_n+1= y_n+hf(x_n,y_n) , n=0,1,2,.... (7)

Приведенная формула определяет т.н. метод Эйлера, имеющий простую геометрическую интерпретацию (рис.1): из точки (x_n , y_n) проводится касательная к искомой кривой y=y(x) до уровня x = x_n+h. Очевидно, что в процессе последовательных переходов по (7) погрешность O(h) существенно возрастает. Поэтому метод Эйлера (7) в чистом виде применяется лишь для грубых оценок при небольшом количестве точек (узлов).

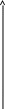
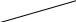y_n+1 y_n+2

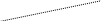
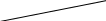
y_n+1

y_n

y_n

x_n x_n+1 x_n x_n+1

Рис.1 Рис.2

Чаще используют модифицированный метод Эйлера, базирующийся на учете трех членов разложения в ряд Тейлора, имеющий погрешность O(h²) и использующий промежуточную точку для коррекции касательной (рис.2):

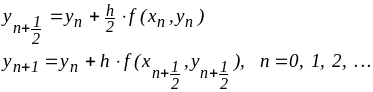(8)

Другая модификация метода Эйлера, называемая модифицированным методом Эйлера-Коши, с той же погрешностью выступает в виде

(9)

Методы Рунге-Кутта.

В отличие от рассмотренных выше методов Эйлера методы Рунге-Кутта учитывают большее количество членов разложения в ряд Тейлора и обладают существенно более высокой точностью (естественно, повышенная точность требует и большего объема вычислений).

Наиболее популярным является метод Рунге-Кутта с погрешностью O(h⁴), реализуемый в виде:

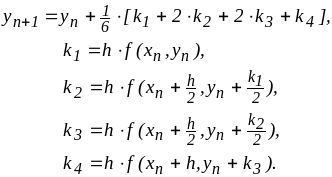(10)

Очевидно, что для обеспечения заданной точности при любом методе необходимо выбрать достаточно малый интервал между смежными значениями x_n и x_n+1 ; однако заранее оценить его так, чтобы и точность достигалась, и объем вычислений был разумным, в общем случае нереально. Поэтому обычно прибегают к системе двойного просчета: сначала делают “прогулку “ по интервалу с шагом h= x_n+1 - x_n , затем берут вдвое меньший шаг и проходят интервал в два приема, сравнивают оценки решения при полном и половинном шаге по критерию точности. Если эти оценки достаточно близки, переходят к очередному интервалу и действуют в нем аналогично ( можно использовать и полученный уменьшенный шаг). В противном же случае уменьшают шаг вдвое и пытаются получить более точную оценку.

Можно использовать и некоторое уточнение оценки решения y_n+1 на основании оценок Y(h) и Y(h/2), полученных при уменьшении шага вдвое

. (11)

Некоторые соображения относительно главной составляющей погрешности [22] и критерия абсолютной/относительной погрешности позволяют несколько уточнить алгоритм метода :

1) отыскиваются оценки Y(h) и Y(h/2) для y_n+1;

2) проверяется выполнение неравенства

D_k=Y(h) - Y(h/2)  ; (12)

3) при невыполнении условия ищут оценку при вдвое меньшем шаге, т.е. повторяют предыдущие действия ; при выполнении такового принимают за решение оценку (11) ;

4) если  > max(D_k) , то продолжать поиск решения для последующих значений аргумента можно с вдвое большим шагом.

Определенными достоинствами обладает и метод Кутта-Мерсона

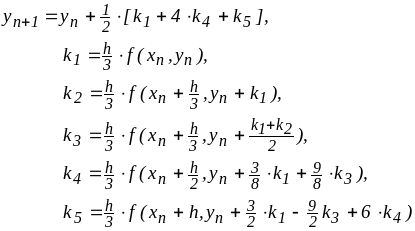(13)

Главный член погрешности определяется величиной

, (14)

где

. (15)

Обратите внимание на то, что эта величина вычисляется при поиске k₅.

Соответственно вычислительная схема метода определяется следующими действиями :

1) при выбранном h по (13) - (14) отыскиваются y_n+1 , W_n+1 и D_n+1;

2) проверяется выполнение неравенства

D_k ,

при невыполнении которого ищут оценку при вдвое меньшем шаге, т.е. повторяют предыдущие действия ;

3) если

32D_k  ,

то последующий поиск решения можно начать с вдвое большим шагом.