Вычисление кратных интегралов. Метод Монте-Карло.

Легко видеть, что при разбиении двумерной области интегрирования по каждой переменной на N частей объем вычислений здесь имеет порядок N².

Если обратиться к вычислению интегралов кратности n, то аналогичный подход требует объема вычислений порядка Nⁿ и при n>3 (есть приложения, где имеют дело с кратностью 10 и выше) о реальных вычислениях помышлять не приходится.

Для области интегрирования S отыскивается n- мерный параллелепипед R = [ a_i  x _i  b _i , i =1,..,n ] такой, что SR, и подвергается “бомбардировке” M случайными, но равномерно распределенными в нем точками

. ( 27 )

Величина

, ( 28 )

где N - количество точек, попавших в S, может быть принята за оценку интеграла.

Для отыскания приемлемого значения N можно воспользоваться законом больших чисел и прийти к оценке [5]

, ( 29 )

где  - заданная абсолютная погрешность,  - вероятность ошибки.

Если задаться погрешностью 0.001 и вероятностью ошибки 0.01, то имеем “фантастическое” значение N=25 000 000 ! Но обратите внимание, что оценка N не зависит от кратности интеграла n. Если область интегрирования является единичным кубом, то при точности порядка 0.001 объем вычислений на равномерной сетке имеет порядок 1000ⁿ и при n>2 эта оценка превышает вышеприведенную. Разумеется, ни о какой бескомпьютерной реализации методов Монте-Карло не может быть и речи.

В составе любой среды программирования имеется датчик случайных чисел, равномерно распределенных в интервале (0,1) . Фактически эти числа являются псевдослучайными .

Для формирования случайной точки n - мерного параллелепипеда берем n очередных случайных чисел 0  z_i  1 ( i=1,..,n) и получаем координаты точки (27)

x_i ^(k) =a_i +( b_i - a_i ) z_i ( i=1,..,n) .

При реальных расчетах величину N числа испытаний выбирают с учетом (29), варьируя ее вдвое или вдесятеро до близости получаемых оценок интеграла.

Заметим, что методы Монте-Карло могут успешно использоваться при решении многих задач, сводящихся к поиску экстремумов функций многих переменных .

Методы Монте-Карло получили “право на существование” лишь с появлением ЭВМ и с учетом постоянного роста их быстродействия становятся вполне рутинным инструментом вычислений. Если на вычисление 20-кратного интеграла в 1959 г. требовалось около получаса машинного счета, то сегодня за это время можно получить оценку с тысячекратно большей точностью.

8. Численное решение обыкновенных дифференциальных уравнений.

Задача Коши: постановка и пути решение.

Пусть требуется найти функцию y=y(x), являющуюся решением обыкновенного дифференциального уравнения

F ( x , y , y’ , y’’ , .. ,y⁽ⁿ⁾ ) = 0 (1)

и удовлетворяющую условиям

y(x₀) = p₀ , y’(x₀) = p₁ , y’’(x₀) = p₂ , ... , y^(n-1)(x₀)=p_n-1 . (2)

( такая задача называется задачей Коши для уравнения (1) ).

Возьмем простейший вариант (1) - линейное уравнение n-го порядка с постоянными коэффициентами

a₀  y⁽ⁿ⁾+ a₁  y^(n-1)+ a₂  y^(n-2)+ ... + a_n-1  y’+ a_n  y = f(x) . (3)

Известно, что общее решение (3) складывается из решения соответствующего однородного уравнения

a₀  y⁽ⁿ⁾+ a₁  y^(n-1)+ a₂  y^(n-2)+ ... + a_n-1  y’+ a_n  y = 0 (4)

и частного решения (3).

Для поиска общего решения однородного уравнения возьмем y=e^kx и подстановкой в (4) получаем т.н. характеристическое уравнение

a₀  kⁿ+ a₁  k^n-1+ a₂  k^n-2+ ... + a_n-1  k+ a_n = 0 (5)

и, если удастся найти корни этого алгебраического уравнение ( методом Ньютона или каким-то другим ), представить искомое решение в виде

(6)

Заметим, что для комплексно-сопряженных корней k = a  b i соответствующие слагаемые в (6) заменяются на

e^ax(С₁Cos(bx)+C₂Sin(bx) ) .

Если обнаруживается m кратных (совпадающих) корней, соответствующие слагаемые в (6) заменяются на

e^kx(С₁ + C₂x + ... +C_m-1 x^m-1 ) .

Например, для уравнения

y’’’ - 6  y’’ + 4  y’ - 24  y = 0

соответствующее характеристическое уравнение выступает в форме

k³ - 6  k²+4  k - 24 = 0 .

Его корни равны 6 , 2 i и -2 i и общее решение уравнения имеет вид

.

Несколько сложнее решается проблема поиска частного (какого-нибудь) решения неоднородного уравнения.

Если его правая часть f(x) является алгебраическим многочленом m-ой степени, то можно воспользоваться методом неопределенных коэффициентов; представить решение многочленом той же степени, подставить в уравнение и приравнять коэффициенты при соответствующих степенях.

Так для уравнения

y’’’ - 6  y’’ + 4  y’ - 24  y = 48 x²+8x+20

берем y*(x)= Ax²+Bx+C и в результате подстановки и приравнивания коэффициентов получаем систему

-12 A + 4 B - 24 C =20

8 A - 24 B = 8

- 24 A = 48 ,

откуда A=-2 , B=-1 , C=0 , т.е. общее решение данного уравнения имеет вид:

-2x²-x .

Если поставить задачу Коши для приведенного уравнения с условиями при x₀=0

y(0)= 1 , y’(0) = 0 , y’’(0) = 0 ,

то возникает система

y(0)= C₁ + C₂ =1

y’(0)= 6C₁ + 2C₃ -1 =0

y’’(0)=36C₁ - 4C₂ - 4 =0 ,

откуда находим

C₁ =0.2 , C₂ =0.8 , C₃ = -0.1 .

Если правая часть (3) - тригонометрический многочлен, то подход к решению аналогичен рассмотренному. В более общем случае при выборе класса функций, описывающих искомое решение, остается надеяться на интуицию и накопленный опыт решения подобных задач.

Если мы имеем дело с задачей для нелинейного уравнения, то, за исключением частных случаев, не следует питать надежд на получение решения в аналитической форме и разумнее сразу обратиться к поиску численного решения.

Заметим, что решение задачи для уравнения n-го порядка можно свести к решению системы n уравнений первого порядка. Так задача для уравнения (3) с начальными условиями (2) может быть представлена в виде:

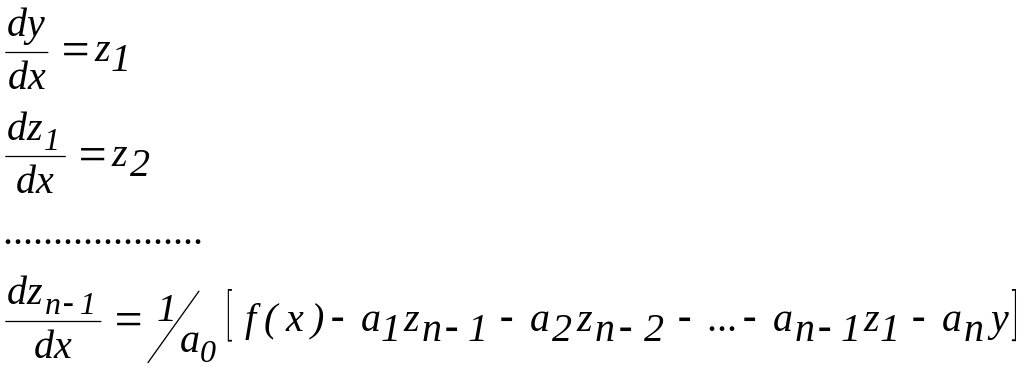
и

y(x₀) = p₀ , z₁(x₀) = p₁ , z₂(x₀) = p₂ , ... , z_n-1(x₀)=p_n-1 .