Интерполирование сплайнами.

при Поэтому для уменьшения погрешности иногда предпочитают область интерполяции разбить на несколько подынтервалов и на каждом из них использовать для аппроксимации полином невысокой степени, т.е. прибегают к кусочно-полиномиальной аппроксимации.

Один из способов такой аппроксимации базируется на т.н. интерполяции сплайнами [2,9] .

Пусть интервал [a,b] разбит на N подынтервалов с граничными узлами a=x₀ < x₁ < ... < x_N-1 < x_N=b .

Сплайном m-го порядка для f(x) на [ a,b ] называют кусочную функцию P(x) = { P₁(x),P₂(x),...,P_N(x) }, удовлетворяющую условиям:

1) все функции P_k(x) (k=1,2,...,N) - полиномы m-го порядка;

2) на концах подынтервалов соблюдаются условия интерполяции и непрерывности

P₁(x₀)=f(x₀),

P(x_k)=P_k+1(x_k)=f(x_k) , k=1,2,...,N-1 , (48)

P_N(x_N)=f(x_N);

3) на концах подынтервалов соблюдаются условия непрерывности производных до m-1-го порядка

P_k^(s)(x_k) = P_k+1^(s)(x_k) , k=1,2,...,N-1 , s=1,...,m-1. (49)

Если взять простейшую задачу - аппроксимацию линейными сплайнами (m=1)

P_k(x)=A_kx+B_k , k=1,2,...,N , (50)

то из (48) возникает система 2N уравнений c 2N неизвестными

A_1 x₀ + B₁= f(x₀),

A_k x_k + B_k = f(x_k), k=1,2,...,N, (51)

A_k+1x_k+B _k+1=f(x_k), k=1,2,...,N-1,

решение которой тривиально

(52)

При аппроксимации квадратичными сплайнами

P_k(x)=A_k(x-x_k-1)²+B_k(x- x_k-1) +C_k , k=1,2,...,N , (53)

возникает система 3N-1 уравнений с 3N неизвестными

_C_k= f(x_k-1), k=1,2,...,N,

A_k(x_k-x _k-1)²+B_k(x_k-x _k-1) +C_k= f(x_k), k=1,2,...,N,

2A_k(x_k-x _k-1)+B_k= B_k+1 , k=1,2,...,N-1.

Недостающее уравнение получают, ставя какое-нибудь условие на одном из концов интервала, например, требуя обращения в нуль первой производной при x= x₀ , откуда B₁= f(x­­₀) =0 . Можно и прибегнуть к более точной оценке производной : например, если x₁=x₀+h и x₂=x₀+2h, то можно принять (см. методы численного дифференцирования) f(x­­₀)=[-3f(x₀)+4f(x₁)-f(x₂)]/2h или аналогичные аппроксимации.

Таким образом,

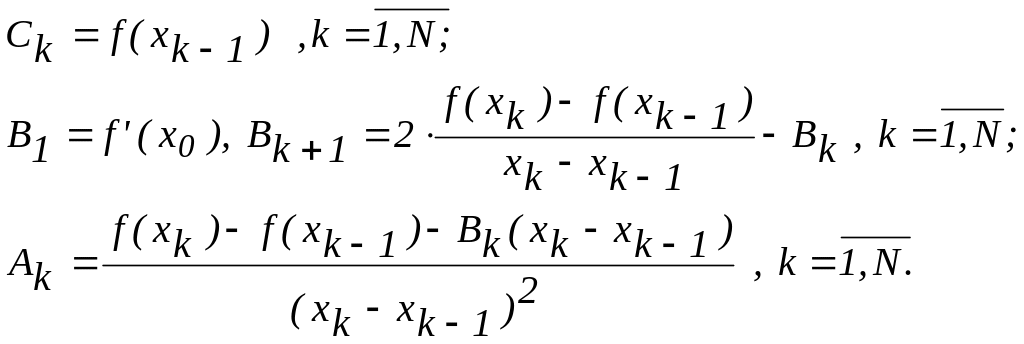(48)

Аналогично можно получить параметры кубической сплайн-интерполяции [15]. Сплайны более высокого порядка практически никто не использует. Достоинством сплайнов степени выше первой является возможность простой и достаточно хорошей оценки не только функции, но и ее производных. Интерполяция сплайнами может облегчить и процесс численного интегрирования.

7. Численное интегрирование.

Если для функции f(x), определенной на [a,b], удается найти первообразную F(x) (“взять интеграл”), то значение интеграла от этой функции с легкостью определяется по формуле Ньютона

. ( 6 )

Для большинства функций поиск первообразной нереален, не говоря уж о табличных функциях, и потому возникает задача численной оценки интеграла с какой-то точностью.

Квадратурные формулы Ньютона-Котеса, Чебышева, Гаусса.

Квадратурные формулы Ньютона-Котеса

Построение квадратурных формул - формул численного интегрирования функций одной переменной базируется на замене исходной функции аппроксимирующей функцией, интеграл от которой легко берется.

Так для функции f(x), вычисленной в каких-то точках x₀ ,x₁ ,...,x_m промежутка [a,b], можно построить многочлен Лагранжа

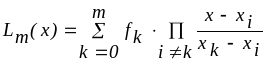
и в результате интегрирования получить квадратурную формулу

, ( 7 )

где R_m[f] - ошибка квадратур и

( 8 )

Хотя идея квадратур связана с интерполяционным многочленом Лагранжа, можно обойтись без его интегрирования.

Заметим, что для многочленов степени не выше m квадратура (7) является точной, т.е. R_m[f] =0 .

Полагая f(x) = x^L ( L=0, 1, 2, ... , m), подстановкой в (7) получаем систему линейных уравнений для определения коэффициентов квадратурной формулы на выбранной системе узлов

. ( 9 )

Большинство известных квадратурных формул строится на задании системы точек a+kh (k=0,1,..., m), где h=(b-a)/ m. Если пределы интегрирования a и b входят в состав узлов квадратурной формулы (7) , то ее называют квадратурой открытого типа (в противном случае - замкнутого типа). Создаваемые таким образом формулы называются формулами Ньютона-Котеса.

Рассмотрим пример построения какой-то квадратуры.

Создадим формулу открытого типа с тремя внутренними узлами a+h, a+2h, a+3h , где h=(b-a)/4 . Построив и решив систему

,

получаем формулу вида

. (10 )

Создадим формулу закрытого типа с тремя узлами a, (a+b)/2, b . Построив и решив систему

,

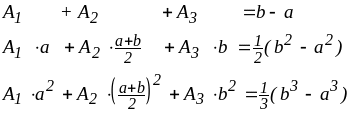получаем известную формулу парабол ( формулу Симпсона )

. (11)

Если взять два узла a, b , то получаем формулу трапеций

. (12 )

Можно построить множество подобных формул, но без суждения о величине остаточного члена это будет искусством ради искусства.

Если представить квадратуры Ньютона-Котеса в стандартных формах:

1) для закрытого типа

, ( 13 )

2) для открытого типа

( 14 )

то можно легко построить любую из них с помощью таблиц

Что касается остаточных членов квадратурных формул, то их оценки зависят от четности числа (n) узлов формулы и типа (s=0 - закрытого и s=1 - открытого)

- n нечетно ; ( 15 )

- n четно ( 16 )

(преимущество формул с нечетным числом узлов очевидно). Значения P и Q приведены в табл..

Обычная практика квадратур отнюдь не предполагает применения квадратурной формулы ко всему промежутку интегрирования. Если имеется оценка максимума соответствующей производной, то из выражения остаточного члена можно найти значение шага Н, разделить интервал на отрезки длины H и отыскать сумму квадратур по этим отрезкам.

Квадратурные формулы Чебышева

П.Л. Чебышевым была предложена группа квадратурных формул с неравноотстоящими узлами, но c одинаковым весом слагаемых

( 17 )

Очевидно, что эта формула применима к любому интегралу, т.к.

.

Требуя, чтобы эта формула была точной для многочленов 1, t, t²,.., tⁿ , получаем систему нелинейных уравнений:

( 18 )

Очевидно, что A=2 / n . Доказано, что приведенная система имеет действительные решения при значениях n  7 и n=9 , причем имеет место симметрия t_k = t_n-k+1 ( k=1,2,...,n/2 ).

Остаточный член квадратурной формулы Чебышева

, ( 19 )

где p(n) / q(n) приведены в табл.

Квадратурные формулы Гаусса

Квадратурные формулы Гаусса отличаются от формул Ньютона-Котеса и Чебышева тем, что здесь подлежат определению и узлы интегрирования, и весовые коэффициенты.

Как было показано выше, всякий интеграл по конечному промежутку можно свести к интегралу по промежутку от -1 до 1

. ( 20 )

Возьмем квадратурную формулу

( 21 )

и потребуем, чтобы она была точной для многочленов до 2n-1-го порядка (например, 1, t, t², ..., t^2n-1). Выполнение этого требования порождает систему 2n нелинейных уравнений с 2n неизвестными, решение которой отнюдь нетривиально даже с учетом симметрии узлов и коэффициентов

t_k = t_n-k+1 , С_k = С_n-k+1 ( k=1,2,...,n/2 ).

( при n=1 и n=2 формула Гаусса совпадает с формулой Чебышева).

Остаточный член n-точечной формулы Гаусса имеет вид [1]:

. ( 22 )

Сравнение этой оценки с оценками для других квадратур показывает преимущество формул Гаусса.