Интерполирование на неравномерной сетке
Выше мы утверждали, что погрешность интерполяционного многочлена Лагранжа определяется величиной
Rn(f)= .
Если максимум n+1-й производной нам неподвластен, то произведение значений (x-xi) в ряде случаев (мы знаем функцию и желаем заменить ее более простой) существенно зависит от выбора узлов интерполирования.
П.Л.Чебышев доказал,
что для t[-1,1]
минимум Q(t)=
достигается при выборе узлов –1
x0<x1<...<xn
1 так, чтобы
Q(t)=Tn+1(t)/2n.
Соответственно, максимум |
Q(t)
|=2-n.
Соответственно, интерполяционный многочлен n-й степени с узлами интерполяции
(4
обеспечивает по точности лучшую интерполяцию, чем интерполяция на равномерной сетке.
Есть еще и другие соображения, связанные с использованием узлов Чебышева.
Казалось бы, с ростом числа узлов максимум Rn(f)0 и значения многочленов Лагранжа все ближе к “истинным” значениям функции, однако производные для многих функций не являются ограниченными и последовательность Rn(f) расходится - феномен Рунге [17]. Например, построив многочлен Лагранжа для функции f(x)=1 /(1+10x2) при равномерном выборе n=11 узлов в интервале [-1,1] , обнаруживаем близ концов интервала семикратное отклонение его значений от истинных (рис.6). При выборе того же количества узлов по Чебышеву осцилляция значений полинома сохраняется, но в пределах разумного.
Интерполирование функций двух переменных.
Пусть задана таблица значений функции двух переменных z=f(x,y) и требуется найти z=f(x*,y*) .
Эта задача решается в два этапа: сначала для всех табличныx значений yk проводится интерполяция по x для указанного x* и затем по найденной табличке значений f(x*,yk) проводится интерполяция по y для заданного y*.
Численное дифференцирование.
Задача численного дифференцирования возникает в случае, когда функция задана таблично или сложным аналитическим выражением.
Большинство формул численного дифференцирования получается дифференцированием интерполяционных формул.
Так, получив интерполяционный многочлен Лагранжа, обычным дифференцированием можно получить его производные любого порядка (не следует только забывать о возможном возрастании погрешности).
Дифференцированием формулы Ньютона интерполирования вперед с последующим заданием t=0 можно получить оценки
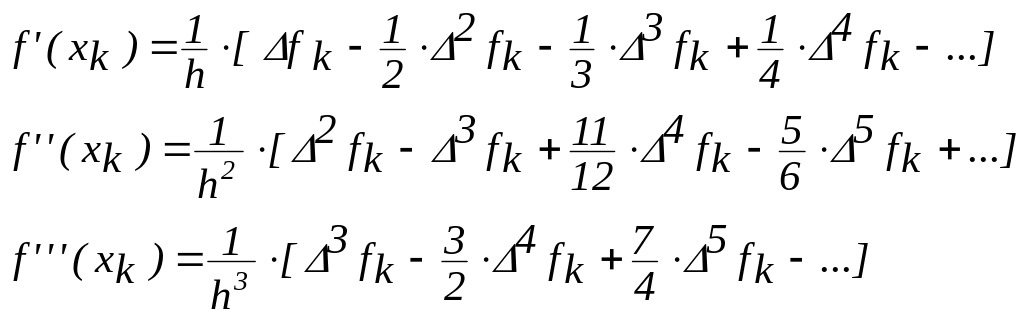( 1 )
На практике редко учитывают разности высоких порядков и используют небольшое число слагаемых. Если найти первые члены разложения функции в ряд Тейлора, то можно получить простые и эффективные в приложениях оценки:
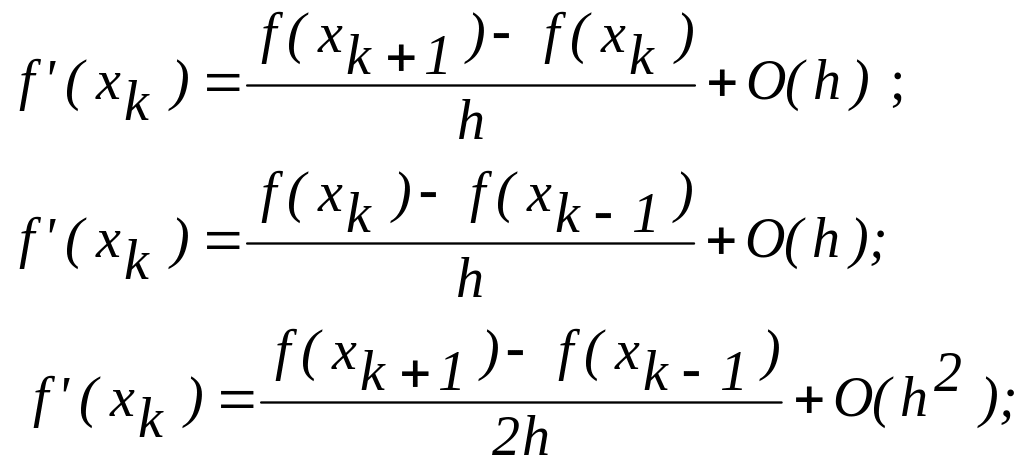( 2 )
( 3 )
Множество подобных и более точных формул численной оценки производных для табличных функций (случай равноотстоящих узлов) приведено в [3] . Этими оценками можно пользоваться при дифференцировании как в середине, так и на концах таблицы.
Для построения формул численного дифференцирования можно использовать и метод неопределенных коэффициентов.
Обозначим для краткости f(xk)=fk . Пусть
f’(xk)=A0 f0+A1 f1+...+Am fm ( 4 )
Полагая, что эта формула точна для полинома m-й степени и, в частности, для полиномов
1 , x- xk , (x- xk)2, . . . , (x- xk)m, ( 5 )
подстановкой этих полиномов в указанную формулу получаем систему m+1 уравнений для определения неопределенных коэффициентов.