Интерполяционные формлы.

Интерполяционные формулы позволяют отыскивать значения табличной функции в точках, отличных от узлов таблицы, без построения интерполяционного многочлена.

Самыми популярными из них являются интерполяционные формулы Ньютона.

Формула Ньютона интерполирования вперед

удобна для использования в диапазоне узлов, удаленных от конца таблицы, и узел x_k подбирают для конкретного значения x так, чтобы величина t = (x- x_k) / h принимала значения в диапазоне от 0 до 1 .

Формула Ньютона интерполирования назад

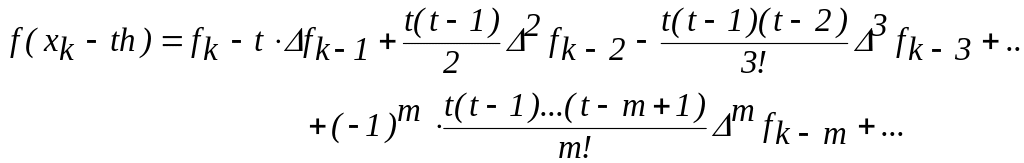удобна для использования в диапазоне узлов, удаленных от начала таблицы, и узел x_k подбирают для конкретного значения x так, чтобы величина t = (x_k - x) / h принимала значения в диапазоне от 0 до 1.

Пример. Пусть задана функция и ее конечные разности [ 3 ]

x k	f k	 f k	2f k	3f k	4f k
0.1	0.09983	0.09884	-0.00199	-0.00096	0.00002
0.2	0.19867	0.09685	-0.00295	-0.00094
0.3	0.29552	0.09390	-0.00389
0.4	0.38942	0.09001
0.5	0.47943

При поиске f(0,14) разумнее выбрать начальный узел x=0.1 (h=0.4) и воспользоваться интерполированием вперед

При поиске f(0,45) разумнее выбрать начальный узел x=0.5 (h=0.5) и воспользоваться интерполированием назад

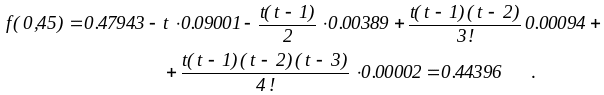
При интерполировании в середине таблиц можно пользоваться и другими интерполяционными формулами, которые строятся на основе конечных разностей, последовательно выбираемых из выделенных клеток приведенной таблицы.

	xk-3	f k-3	f k-3	2f k-3	3f k-3	4f k-3	5f k-3
	x k-2	f k-2	fk-2	2f k-2	3f k-2	4f k-2	5fk-2
	xk-1	f k-1	f k-1	2f k-1	3f k-1	4f k-1
	xk	fk	fk	2fk	3fk
	xk+1	f k+1	f k+1	2f k+1
	xk+2	f k+2	f k+2
	x k+3	fk+3

Примерами таких формул могут служить следующие представления, где 0 < t < 1 :

интерполяционные формулы Гаусса

интерполяционная формула Стирлинга

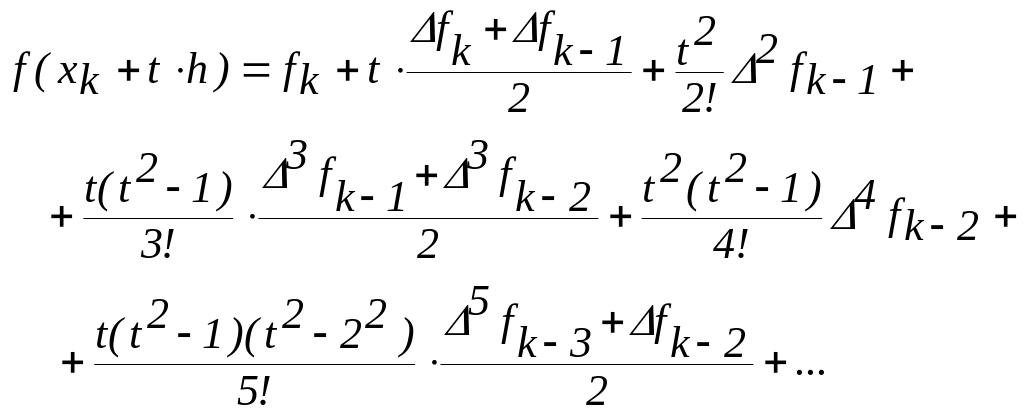
интерполяционная формула Бесселя

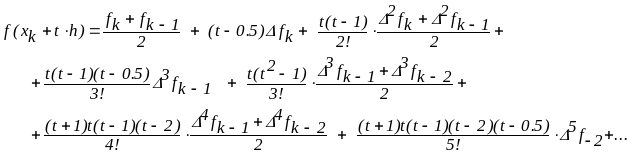Существуют и другие представления этих формул с использованием т.н. центральных разностей, первая из которых определяется формулой

²f(x)= f(x+h/2) - f(x-h/2) .