14)Сущность средней величины и условия ее применения
Средней величиной статистики называется обобщающая характеристика совокупности однотипных явлений по какому-либо признаку.
Среднее показывает характерную, типичную величину признака у единиц совокупности.
Средние, которые относятся к статистике относятся к классу степенных средних.
Средняя величина - обобщающий показатель, характеризующий уровень варьирующего признака в расчете на единицу однородной совокупно; в конкретных условиях места и времени.Исчисление средних величин предполагает выполнение следующих требований:1) качественная однородность совокупности, по которой исчислена средняя.
2) исключение влияния на исчисление средней величины случайных, сугубо индивидуальных причин и факторов. 3) при вычислении средней величины важно установить цель ее расчета и так называемый определяющий показатель (свойство), на который она должна быть ориентирована. Определяющий показатель может выступать в виде суммы значений осредняемого признака, сунны его обратных значений и т. п. Средняя, рассчитанная по совокупности в целом, называется общей средней, средние, исчисленные для каждой группы, - групповыми средними. Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления, складывающуюся в конкретных условиях данной группы.С помощью метода средних решаются следующие задачи:
1) характеристика уровня развития явлений;
2) сравнение двух или нескольких уровней;
3) изучение взаимосвязей социально-экономических явлений;
4) анализ размещения социально-экономических явлений в пространстве.
15)Виды средних величин и их применение в анализе экономических явлений
Средняя арифметическая (простая) применяется, когда общий объем варьирующего признака для всей совокупности образуется как сумма значений признаков у отдельных ее единиц. Ее вычисление сводится ксуммирование всех значений варьирующего признака и делению полученной суммы на общее количество единиц совокупности:
Средняя арифметическая (взвешенная) используется в тех случаях, когда известны отдельные значения признака и их веса (fi):
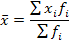где
хi - варианты осредняемого признака; fi-
частота, которая показывает, сколько
раз встречается i-oe значение в совокупности.
Средняя
геометрическая (простая):
Средняя
геометрическая (взвешенная):
Средняя квадратическая применяется при расчете с величинами квадратных функций, используется для измерения степени колеблемостииндивидуальных значений признака вокруг средней арифметической в рядах распределения и исчисляется по формулам:
(простая)
(взвешенная)
16)Средняя арифметическая и условия ее применения
Средняя арифметическая применяется в тех случаях, когда объем варьирующего признака всей совокупности образуется как сумма значений этого признака у ее отдельных единиц.
Формулы и техника расчетов следующие:
простой средней арифметической (невзвешенной)
взвешенной средней арифметической
17)Средняя гармоническая и средняя геометрическая, методы их расчета
Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т. е. характеризует средний коэффициент роста.
Средняя геометрическая (простая):
Средняя геометрическая (взвешенная):
Средняя гармоническая
Определяющее свойство средней гармонической заключается в том, чтобы при осреднении оставалась неизменной сумма величин, обратных осредняемым.
Простая Взвешенная
