23)Индивидуальные и общие индексы

Индивидуальные индексы получают в результате сравнения однотоварных явлений. Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. В зависимости от экономического назначения индивидуальные индексы бывают: физического объема продукции, себестоимости, цен, трудоемкости и т.д.

Индекс физического объема продукции: показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько процентов составляет.

Индивидуальный индекс цен: характеризует изменение цены одного определенного товара в текущем периоде по сравнению с базисным.

Индивидуальный индекс себестоимости единицы продукции: показывает изменение себестоимости.

Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих статистическую совокупность и обладают следующими свойствами:

-синтетические – посредством индексного метода производится соединение (агрегирование) в целом разнородных единиц статистической совокупности;

-аналитические – посредством индексного метода определяется влияние факторов на изменение изучаемого показателя.

Примером неоднородной совокупности является общая масса проданных товаров нескольких видов. Тогда сумма выручки может быть записана в виде агрегата – это сумма произведений взвешивающего показателя на объемный:

24. Методы вычисления агрегатных индексов. Индексы Ласпейреса, Пааше, Фишера

ФишераРассмотрим принцип построения агрегатных индексов качественных показателей на примере индекса цен.Если нам необходимо выявить изменения цен на различные продукты и товары или количества товаров и продуктов, то необходимо привести определенное количество товаров и продуктов по определенным ценам к общей стоимостиНо возникает проблема: на уровне какого периода зафиксировать данные (базисного или отчетного).

Существует два способа расчета индексов цен: индексы цен Лайспейреса и Пааше

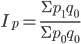
Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но на товары реализованные в базисном периоде

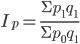Индекс цен Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде.

Идеальный индекс Фишера

Представляет собой среднюю геометрическую из произведений двух агрегатных индексов цен Ласпейреса и Пааше:

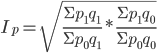Лайсп индексVпродаж: Iq=∑p0q1/∑p0q0 Паше: Iq=∑p1q1/∑p1q0

25)Преобразование агрегатных индексов в средние индексы

Агрегатный способ исчисления общих индексов является основным, но не единственным. В некоторых случаях отдельные сведения, необходимые для расчета агрегатного индекса могут отсутствовать. Например, количественный учет продажи продукции или товаров осуществляется не везде. Нередко реализация продукции и товаров, учитывается в стоимости (денежном) выражении. Поэтому агрегатная форма общего индекса в таких случаях не может применяться.

Здесь используется второй способ расчета общих индексов, суть которого состоит в следующем: рассчитываются индивидуальные индексы, а затем из них рассчитывается средний взвешенный индекс, но при этом способе расчета нужно правильно взять форму средней и систему весов для индивидуальных индексов.

Руководствуясь общим правилом, что агрегатный индекс является основой любого общего индекса, формируется следствие: средний взвешенный из индивидуальных индексов должен быть тождествен исходному агрегатному. Другими словами, средние из индивидуальных индексов выступают как преобразованная форма агрегатного индекса. Доказано, что агрегатный индекс может быть преобразован только или в средний арифметический, или в средний гармонический из индивидуальных индексов.

Отсюда делается вывод: что при исчислении средних индексов могут быть использованы только две формы средних: средняя арифметическая и средняя гармоническая индивидуальных индексов.