7. 3. Транспортная задача

Рассмотрим еще один пример применения средства Поиск решения. Фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики располагаются в Денвере, Бостоне, Нью-Орлеане и Далласе с производственными возможностями соответственно 200, 150, 225 и 175 единиц продукции ежедневно. Распределительные центры располагаются в Лос-Анджелесе, Далласе, Сент-Луисе, Вашингтоне и Атланте с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике не поставленной в центр распределения единицы продукции обходится в $0,75 в день, а штраф за просрочку поставки заказанной потребителем в центре распределения единицы продукции, но там не находящейся, равен $2,5 в день. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в табл. 7.3.

Таблица 7.3

Транспортные расходы

	1 Лос-Анджелес	2 Даллас	3 Сент-Луис	4 Вашингтон	5 Атланта	Производство
1 Денвер	1,5	2	1,75	2,25	2,25	200
2 Бостон	2,5	2	1,75	1	1,5	150
3 Нью-Орлеан	2	1,5	1,5	1,75	1,75	225
4 Даллас	2	0,5	1,75	1,75	1,75	175
Потребность	100	200	50	250	150

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

Для решения данной задачи построим ее математическую модель. Неизвестными здесь являются объемы перевозок: Пусть х_ij — объем перевозок с i-ой фабрики в j-ый центр распределения. Функцией цели являются суммарные транспортные расходы, т. е.

где с_ij — стоимость перевозки единицы продукции с с i-ой фабрики в j-ый центр распределения. Кроме того, неизвестные должны удовлетворять следующим ограничениям:

• неотрицательность объема перевозок;

• т. к. модель сбалансирована, то вся продукция должна быть вывезена с фабрик, и потребность всех центров распределения должна быть полностью удовлетворена.

Таким образом, мы имеем следующую модель:

минимизировать

при ограничениях:

где а_i – объем производства на i-ой фабрике; b_j – спрос в j-ом центре распределения.

Выполните следующую подготовительную работу для решения транспортной задачи с помощью средства Поиск решения (рис. 7.7).

1. Введите в ячейки диапазона В3: F6 стоимости перевозок.

2. Отведите ячейки диапазона В8:F11 под значения неизвестных (объемов перевозок).

3. Введите в ячейки диапазона Н8:Н11 объемы производства на фабриках.

4. Введите в ячейки диапазона В13:F13 потребность в продукции в пунктах распределения.

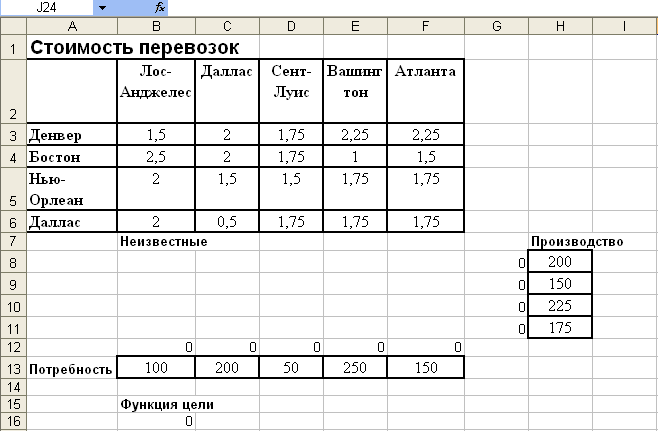
Рис. 7.7. Исходные данные для транспортной задачи

4. В ячейку В16 введите функцию цели

=СУММПР0ИЗВ(ВЗ:F6;В8:F11)

6. В ячейки диапазонов G8:G11 введите формулы, вычисляющие объемы производства на фабриках, в ячейки диапазона B12:F12 объемы доставляемой продукции в пункты распределения. А именно:

Ячейка	Формула	Ячейка	Формула
G8	=CУMM(B8:F8)	B12	=СУММ(В8:В11)
G9	=CУMM(B9:F9)	C12	=СУММ(С8:С11)
G10	=CУMM(B10:F10)	D12	=CУMM(D8:D11)
G11	=CУMM(B11:F11)	E12	=СУММ(Е8:Е11)
		F12	=CУMM(F8:F11)

7. Выберите команду Сервис – Поиск решения и заполните диалоговое окно Поиск решения, как показано на рис. 7.8.

8. Нажмите кнопку Выполнить. Средство Поиск решения найдет оптималь­ный план поставок продукции и соответствующие ему транспортные рас­ходы (рис. 7.9).

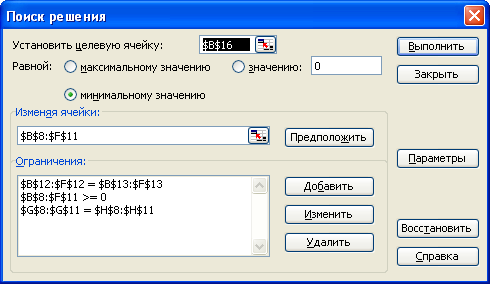
Рис. 7.8. Заполненное диалоговое окно Поиск решения для транспортной задачи

Рис. 7.9. Оптимальное решение транспортной задачи