6. Массивы в Excel

Часто при работе с таблицами возникает необходимость применить одну и ту же операцию к целому диапазону ячеек или произвести расчеты по формулам, зависящим от большого массива данных. Под массивом в Excel понимается прямоугольный диапазон формул или значений, которые программа обрабатывает как единую группу. Excel предоставляет простое и элегантное средство – формула массива – для решения задач, которые будут представлены в данном разделе.

Расчет НДС, как пример умножения элементов массива на число

В качестве примера использования формулы массива приведем расчет цен группы товаров с учетом налога на добавленную стоимость (НДС). Пусть, например, в диапазоне ячеек В2:В4 даны цены группы товаров без учета НДС. Необходимо найти цену каждого товара с учетом НДС (который будем полагать равным 25%). Таким образом, необходимо умножить массив элементов в ячейках В2:В4 на 125%. Результат надо разместить в ячейках диапазона С2:С4 (рис.5.1). Необходимо выполнить следующие действия:

1. Выберите диапазон, например, С2:С4, в котором будет размещен результат умножения первоначального массива на число. От диапазона, в котором будет находиться результат, требуется, чтобы он имел тот же размер, что и исходный диапазон (рис. 6.1).

2. Введите формулу:

=В2:В4*125%

3. Завершите ввод формулы не нажатием клавиши <Enter>, а нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Таким образом, вы сообщите Excel, что необходимо выполнить операцию над массивом, т.е. создать формулу массива. В ответ Excel автоматически возьмет формулу в фигурные скобки (рис. 6.2): {=B2:B4*125%}

Рис. 6.1. Выделение диапазона для ввода результирующего массива

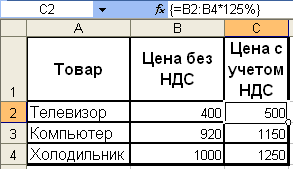
Рис. 6.2. Умножение элементов массива на число

Поэлементное сложение, вычитание, умножение и деление двух массивов

Продемонстрируем операцию поэлементного сложения двух массивов. Пусть, например, слагаемыми будут массивы, содержащиеся в диапазонах А1:В2 и D1:E2 (рис. 6.3).

1. Выберите на рабочем листе диапазон, например G1:H2, в который будет помещен результат поэлементного сложения двух массивов. От данного диапазона требуется, чтобы он имел тот же размер, что и массивы-слагаемые.

2. Введите формулу

=А1:В2+D1:E2

3. Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки (рис. 5.3) и произведет требуемые вычисления

{=А1:В2+D1:E2}

Рис. 6.3. Сумма двух массивов

Аналогично можно вычислить поэлементно разность, произведение и деление массивов.

Вычисление функции, зависящей от элементов массива

На рабочем листе допустимо создавать формулы массива, каждый элемент которого связан посредством некоторой функции с соответствующим элементом первоначального массива.

Например, пусть в диапазоне А1:В2 имеется некоторый массив данных. Требуется найти массив, элементы которого равны значениям функции sin от соответствующих элементов искомого массива.

Для этого:

1. Выберите в рабочем листе диапазон, например D1:E2, в котором будет размещен результат. От данного диапазона требуется, чтобы он имел тот же размер, что и исходный диапазон.

2. Введите формулу

=SIN(A1:B2)

3. Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива

{=SIN(A1:B2)}

Вычисление сложных выражений

Приведем более сложный пример использования формул массива. А именно, попытаемся найти значение следующего выражения:

,

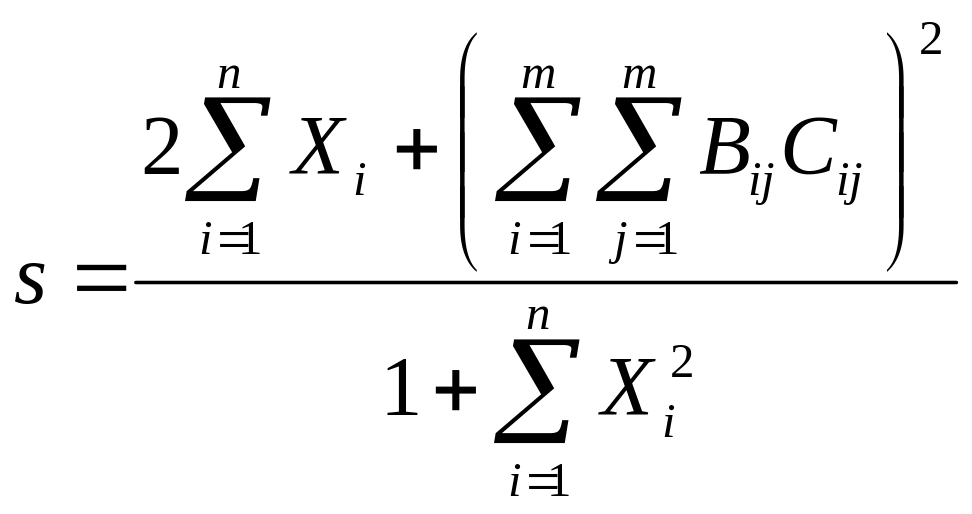где Х – вектор из n компонентов, В и С – матрицы размера mxm, причем, n=3, m=2 и

Для решения этой задачи нам потребуется функция рабочего листа СУММ, которая суммирует все числа из диапазона ячеек.

Для вычисления значения s можно выполнить следующие действия:

1. Введите в диапазон А2:А4 компоненты вектора Х.

2. Введите в диапазон В2:С3 компоненты матрицы В.

3. Введите в диапазон D2:E3 компоненты матрицы С.

4. Введите в ячейку В6 следующую формулу:

=(2*СУММ(А2:А4)+СУММ(В2:С3*D2:E3)^2)/(1+СУММ(А2:А4^2))

5. Завершите ввод нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления (рис.6.4)

{=(2*СУММ(А2:А4)+СУММ(В2:С3*D2:E3)^2)/(1+СУММ(А2:А4^2))}

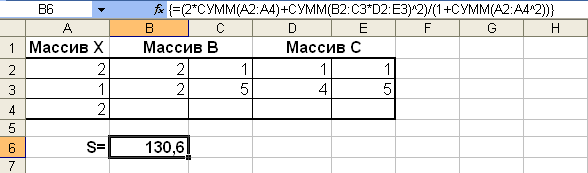
Рис.6.4. Вычисление значения s

Конечно, этот же результат можно было бы получить и без использования формул массивов, введя в ячейку В6 простую формулу:

=(2*СУММ(А2:А4)+СУММПРОИЗВ(В2:С3;D2:E3)^2)/(1+СУММКВ(А2:А4))

В данной формуле используются функции рабочего листа СУММПРОИЗВ и СУММКВ.

Функция СУММПРОИЗВ возвращает сумму произведений соответствующих элементов массивов. Синтаксис:

СУММПРОИЗВ(массив1;массив2; …)

где массив1, массив2, … – это от 2 до 30 массивов, чьи компоненты нужно перемножить, а затем сложить. Аргументы, которые являются массивами, должны иметь одинаковые размеры. Если это не так, то функция СУММПРОИЗВ возвращает значение ошибки #ЗНАЧ!.

Функция СУММКВ возвращает сумму квадратов аргументов. Синтаксис:

СУММКВ(число1;число2; …)

где число1, число2, … – это от 1 до 30 аргументов, квадраты которых суммируются. Можно использовать отдельный массив или ссылку на массив вместо аргументов, разделяемых точкой с запятой.

Функции рабочего листа для работы с матрицами

В Excel имеются функции рабочего листа для работы с матрицами, перечисленные в табл. 6.1.

Таблица 6.1.

Функции обработки матриц

Функция	Описание
МОБР(массив)	Возвращает обратную матрицу
МОПРЕД(массив)	Возвращает определитель матрицы
МУМНОЖ(массив1;массив2)	Возвращает матричное произведение двух матриц
ТРАНСП(массив)	Возвращает транспонированную матрицу

Замечание. При работе с матрицами, перед вводом формулы, надо выделить область на рабочем листе, куда будет помещен результат вычислений, а ввод формулы завершать нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>.

Решение системы линейных уравнений

Решим в качестве примера систему линейных уравнений с двумя неизвестными, матрица коэффициентов которой записана в ячейки А2:В3, а свободные члены – в ячейки D2:D3 (рис. 6.5).

Вспомним, что решение линейной системы АХ = В, где А – матрица коэффициентов, В – столбец (вектор) свободных членов, Х – столбец (вектор) неизвестных, имеет вид Х = А^-1В, где А^-1 – обратная матрица к А.

В нашем случае

.

Поэтому для решения системы уравнений

1. Выберите тот диапазон, в который будет введено решение. Например, F2:F3.

2. Введите в него формулу

=МУМНОЖ(МОБР(А2:В3);D2:D3)

3. Завершите вод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива (рис. 6.5):

{=МУМНОЖ(МОБР(А2:В3);D2:D3)}

Рис. 6.5. Решение системы линейных уравнений

Таким образом, решением системы уравнений является вектор

В качестве более сложного примера решим систему линейных уравнений

А²Х = В, где

.

Решение этой системы является вектор Х = (А²)^-1В.

Для нахождения вектора Х:

1. Введите элементы матрицы А в диапазон ячеек А2:В3.

2. Введите элементы вектора В в диапазон ячеек D2:D3.

3. Выберите диапазон F2:F3, куда поместим элементы вектора решения.

4. Введите в этот диапазон формулу:

=МУМНОЖ(МОБР(МУМНОЖ(А2:В3; А2:В3));D2:D3)

5. Завершите ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива:

{=МУМНОЖ(МОБР(МУМНОЖ(А2:В3; А2:В3));D2:D3)}

В диапазоне ячеек F2:F3 будет найдено решение системы уравнений

Нахождение значения квадратичной формы

Рассмотрим пример вычисления квадратичной формы , при этом

Для нахождения этой квадратичной формы:

1. Введем элементы матрицы A в диапазоне ячеек А2:В3 и вектора X в диапазоне ячеек D2:D3.

2. Выберем ячейку F2 для вычисления значения формы.

3. Введем формулу:

=МУМНОЖ(МУМНОЖ(ТРАНСП(D2:D3); A2:B3);D2:D3)

4. Завершим ввод формулы нажатием комбинации клавиш <Ctrl>+<Shift>+<Enter>. Excel возьмет формулу в строке формул в фигурные скобки и произведет требуемые вычисления с элементами массива (см. рис. 6.6):

{=МУМНОЖ(МУМНОЖ(ТРАНСП(D2:D3); A2:B3);D2:D3)}

Рис. 6.6. Нахождение значения квадратичной формы

В ячейке F2 будет получено искомое значение формы 196.