28. Интегральная предельна теорема Муавра-Лапласа. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях.

На практике при большом числе испытаний n и не слишком малой вероятности р важно оценить вероятность того, что число появлений события А лежит в некоторых границах. Эту оценку устанавливает интегральная теорема Муавра-Лапласа.

Теорема: пусть m-число наступлений события А в серии из n-независимых испытаний, р –вероятность наступления события А при каждом испытании (0<р<1), тогда вероятность P_n(m₁≤m≤m₂) того, что в этих испытаниях событие А появится не менее m₁ раз и не более m₂ раз, при n→∞ удовл. соотношению:

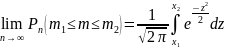
x₁= ; x₂=

При больших значениях m имеет место приближённая интегральная формула Муавра-Лапласа: P_n(m₁≤m≤m₂)=Ф(х₂)-Ф(х₁) (27)

где Ф(х)=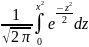

Эта функция называется функцией Лапласа, ё называют интегралом ошибок, она нечётная Ф(-х)= - Ф(х).

Используется в приложении для отрицательных значений х.

Замечание: оценка погрешности при использовании формулы (27) показывает, что хорошая точность обеспечивается уже при значениях npq≥10.

Вероятностью того, что в n независимых испытаниях, в каждом из которых вероятность появления события = р(0<р<1), абсолютная величина отклонения относительной частоты m/n появления события, от вероятности появления события, не привысит положительного числа ε и приближённо равна удвоенной функции Лапласа Х=ε

P(| |≤ε)=2Ф(ε

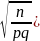
29. Понятие случайной величины. Функция распределения случайной величины, ее свойства.

Случайная величина Х называется действительной фун. X(w) на множ-ве элем –ых исходов Q и такая при любых Х множ-во тех w, для кот x(w)<x принадлежат алгебре событий для данного эксперимента.Скаляр. вел-на Х принадлежит действительным значениям X(w) каждой точке w принадлежащего Q.

Случайные величины: дискретные и непрерывные.

Дискретными наз. Случ. Вел-ну, кот принимает конечное или счетное множ-во значений. Использ-ся при описании измерений принимающих целочисленные значения.

пространство х=х(w)

А=(Х<х) , тогда А явл-ся событием исследования для каждого опеределена вероят-ть P9A)=P(X<x)=F(X) – эта функция распределения случайной величины х. Значение фну-ии распределения в т.Х – вероят-ти события, состаящего в том, что случ. Вел-на Х примет значение <x.

Свойства:

1) F(x) вероят-ть собятия А (Х<x), функция должна быть в этиъ пределах для

2) F(x) монотонно неубывающая функция на всей числовой прямой

3)если случ. Вел-на примет возможное значение с вероятностью ,то ее функция распределения F(x) имеет в точке разрыв 1-го рода называемый скачком, который определяется . В точке непрерывна

4)

Если то событие ( ) невозможно => P( )=0

- достоверно, то P( )=1

Можно показать, что всякая функция, обладающая свойствами 1-4 задает распределение вероятностей на подмножествах от для при этом каждому такому интервалу ставится в соответствии вероятность F(x)

Связь между возмонжными значениями случан.вел-ны и их вероят-тями называют знаконом распределения случ.вел-ны.