26. Повторение испытаний. Схема испытаний Бернулли. Биномиальное распределение вероятностей. Наивероятнейшее число появлений события в независимых испытаниях.
В задачах, связанных с многократным повторением испытаний, в результате из которых может появиться или не появиться некоторое событие А, представляет интерес исход не каждого отдельного испытания, а общее число появлений события А в результате определённого числа опытов.
Последовательные испытания называются независимыми, если вероятность осуществления любого исхода в каждом n-ном испытании не зависит от реализации исходов предыдущих испытаний.
Серию независимых испытаний с одной и той же вероятностью успеха р=р(А) называют испытаниями или схемами Бернулли.
Обозначим Рn(m) – вероятность появления m-раз события А в серии из независимых n- испытаний.
Вероятность того, что в каждом из n-независимых испытаний в которых вероятность появления события 0<р<1, событии наступит ровно m-раз (безразлично в какой последовательности) и будет вычисляться след.образом: Рn(m)=Cnm*pm*qn-m -формула Бернулли
Рn(m)=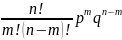
Правило и ф-лы Бернулли – общий член разложения бинома Ньютона.
(q+p)n=qn+Cn1*p*qn-1+Cn2*p2*qn-2+…+Cnm*pm*qn-m+…+pn
Если m=0,1,2,…,n-1,n, то получим соответствующую последовательность вероятностей. Pn(0), Pn(1), …, Pn(n-1), Pn(n)
Совокупность этих вероятностей называется биномиальным распределением вероятностей.
, при этом p+q=1
Биномиальное распределение позволяет определить не только вероятность появления события А m-раз в n-испытаниях, но и вероятность Рn(k≤m≤l) того, что число m-появлений события А заключено на некотором отрезке [k;l], причём 0≤k≤l≤n. В частности, вероятность того, что в n-испытаниях событие наступит: а) менее m-раз Рn(0)+Pn(1)+…+Pn(m-1) б) более m-раз
Рn(m+1)+Pn(m+2)+…+Pn(n) в) не менее m-раз Рn(m)+Pn(m+1)+…+Pn(n)
г) не более m-раз Рn(0)+Pn(1)+…+Pn(m)
Здесь: Рn(0)=qn;
Pn(1)=n*p*qn-1;
Pn(2)=
;
Pn(n)=pn
В силу несовместности некоторых событий, {k,k+1,…,(l-1),l} искомая вероятность Pn(k≤m≤l)=Pn(k)+Pn(k+1)+…+Pn(l-1)+Pn(l)
Число m0 наступлений событий в независимых испытаниях, в каждом из которых вероятность появления события = Р, называют наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях m0 раз превышает или по крайней мере не меньше вероятности остальных возможных исходов испытаний, то имеется по крайней мере одно целое число m0, удовлетворяющее этим неравенствам
np-q≤m0≤np+q.
Из этого получаем:
а) (np-q) –дробное, существует одно наивероятнейшее число m0
б) (np-q) – целое, существует 2 наивероятнейших числа m0, m0+1
в) np – целое, наивероятнейшее число m0=np
27. Распределение Пуассона. Локальная предельная теорема Муавра-Лапласа.
В схеме независимых испытаний при больших n, формула Бернулли приводит к громоздким вычислениям. Задача, где рассматривается большое число n-независимых испытаний, а вероятность р- наступления события А в каждом испытании мала, может быть приближен вычислена вероятность Pn(m) по формуле Пуассона.
Теорема Пуассона:
пусть вероятность события А при каждом
испытании в серии из n-независимых
испытаний =λ/n,
где λ>0 –пост.независ. от n.
Тогда вероятность Pn(m),
при n→∞
и фикс. m,
стремится к величине
-формула
Пуассона
Т.к. в таких испытаниях p-мало, то распределение Пуассона называют законом распределения редких явлений.
Pn(m)=Cnm*pm*qn~ =Pm(λ) - асимптотическая формула Пуассона
Локальная предельная теорема Муавра-Лапласа.
Она устанавливает приближённую формулу для вычисления вероятности Pn(m).
Теорема: пусть
вероятность события А в n-независимых
испытаниях = р, (0<р<1), тогда вероятность
Pn(m)
того, что в этих испытаниях событие А
наступит ровно m-раз
удовлетворяет при n→∞
следующему соотношению:
x=
При больших n имеет место приближённая локальная формула Муавра-Лапласа.
Pn(m)~
(25)
(26)
Формула (25) даёт
удовл.значение вероятности при достаточно
больших значениях n,
а также если р не слишком близка к 0 или
1 (эффективнее всего при р близких к
0,5). Функция
формулы (26) –чётная (
=
),
поэтому в прил. Приведены значения
только для x>0.