10. Диаграмма Хассе как способ задания отношения частичного порядка на множестве. Непосредственно предшествующие элементы. Линейно упорядоченные подмножества.

Пусть .

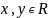Если , то x непосредственно предшествует у. Обознач.: .

Диаграмма Хассе задает схему непосредственных предшественников.

Если вершина явл. непосредственным предшественником , то помещают на ниж. уровне, а на верхнем. Вершины соединяют не направ. дугами.

В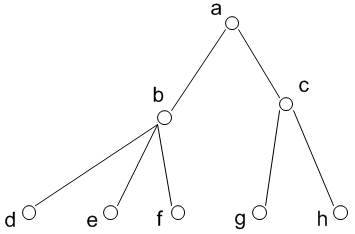 рассмотренном примере .

«быть делителем»: «включение слов друг в друга»:

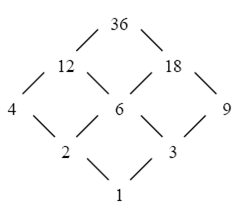
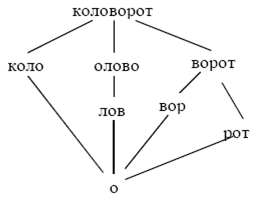
«быть меньше»: «быть подмножеством»:

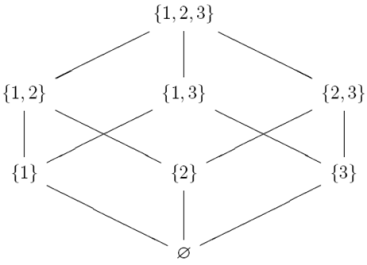
11. Замыкание отношений. Рефлексивное, симметричное, транзитивное замыкание отношений.

— замыкание отношения относ. св-ва , если:

• обладает св-вом ;

• ;

• явл. подмнож. ∀ др. отношения, содержащего и обладающего св-вом .

R — некоторое бинарное отношение на множ. A:

• Рефлексивное замыкание отношения — отношение .

• Симметричным замыканием 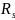отношения называется отношение .

• Транзитивным замыканием отношения называется отношение

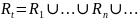
Отношение, включающее свои симметрич., рефлексив. и транзитив. замыкания, явл. отношением эквивалентности (обратное утв. также верное).

12. Понятие нечеткого множества. Функция принадлежности и ее интерпретация. Способы формализации нечетких множеств. Наиболее распространенные параметрические функции принадлежности.

Нечеткое множ. — обобщение обычного, когда хар-ристическая функция (наз. функцией принадлежности) может принимать любые знач. на отрезке [0,1].

Более строго, нечетким множ. наз. совокуп. пар , .

Пусть, например, ,

. Эл-т a не принадлежит множ., эл-т b принадлежит в малой степени, эл-т c более или менее принадлежит, эл-т d принадлежит в значительной степени, e явл. эл-том множ.

# (интерпретация) ф-ции принадлеж.: множ. молодых людей B = {х: х — человек}. До 20 лет человек молод. Возникает вопрос: почему кто-то в свой 20-летний юбилей — молодой, а на следующий — уже нет? Eсли передвигать верхнюю границу на 1 день, то можно задаться таким же вопросом и т.д. до бесконечности.

Более естественный путь получения множ. B состоит в ослаблении строгого разделения на молодых и не молодых.

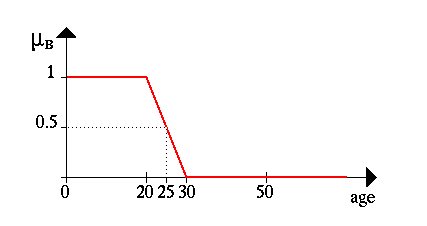
Наиболее распростр. параметрич. ф-ции принадлеж.:

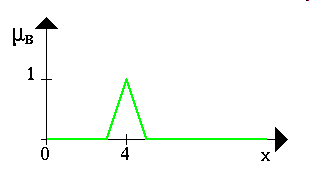
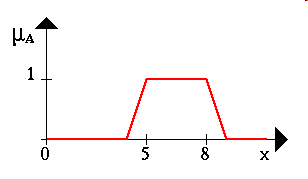
треугольные m(x) = 0, при x <=a; m(x) = (x – a)/(b – a), при a < x <=b; m(x) = (c – x)/(c – b), при b < x <=c; m(x) = 0, при с < x.
трапециевидные m(x) = 0, при x <a; m(x) = (x – a)/(b – a), при a < x <=b; m(x)= 1, при b < x <=c; m(x) = (d – x)/(d – c), при c < x <=d; m(x) = 0, при d < x.
гауссовские зад. 2 парам. (c,s): m(x) = exp(-0.5(x - c)2/s2).
колоколообразные зад. парам. (a,b,c): m(x) = 1/(1+((x - c)/a)2b)

13. Пустое, нормальное и субнормальное нечеткое множество. Точки перехода нечеткого множества. Отношения между нечеткими множествами: включения и равенства. Множество 𝛂–уровня, сильное и слабое сечение.

Множ., не содерж. эл-тов, наз. пустым и обознач. Æ.

Нечеткое множ. А наз. пустым, если , .

Носителем нечеткого множ. А называется подмнож. таких точек U, для которых величина m_A(x) положительна. Носитель обознач. S(A) или SuppA: S(A) = {x|xΠU, m_A(x) > 0}.

Высотой h(A) нечеткого множ. А наз. величина h(A) = max m_A(x)  по всем .

Нормальное нечеткое множ. — высота = единице. В противном случае — субнормально. Нечёткое множ. унимодально, если только на одном .

Эл-ты множ. U, для кот. степень принадлежности m_A(x) = 0.5 наз. точками перехода нечеткого множ.

Отношения между множ-вами:

A содержится в B, если , m_A(x) £ m_B(x).

A и B равны, если , m_A(x) = m_B(x).

Множество a-уровня нечеткого множ. А — множ. А_a всех эл-тов универсума U, степень принадлежности кот. : A_a={x |" xΠU, m_A(x) ³a}.

Множ. a-уровня наз. иногда сечением a нечеткого множ. Причем, если m_A(x) ³ a, то сечение сильное, если m_A(x)  > a — слабое.

14. Основные операции над нечеткими множествами: объединение, пересечение, дополнение, разность, дизъюнктивная сумма, степень множества, концентрирование и растяжение, прямое произведение нечетких множеств. Законы алгебры нечетких множеств при максимином и алгебраическом определении функции принадлежности. Законы алгебры нечетких множеств при ограниченной функции принадлежности.

Объединение нечетких множеств А и В в U — наим. нечеткое подмнож. , включающее и А и В.

Пересечением нечетких множеств А и В в U — наиб. нечеткое подмнож. , содерж. одновременно в А и В.

Дополнение нечеткого множ. А — нечеткое множ. ­–A с функцией принадлежности: m_-A (x) = 1 — m_A(x), " xΠU.

Разность нечетких множеств А и В определяется по-разному, введением двух независимых операций

или m_A - B (x) = min(m_A(x), 1 — m_B(x)), .

Дизъюнктивная сумма АÅВ нечетких множеств определяется " xΠU как mA  Å  B (x) = max[ min(mA(x), 1 — mB(x) ), min(mB(x), 1 — mA(x))]

Степень нечеткого множ. — нечеткое множ. Aα с функцией принадлеж. µ(Aα (x)) = µαA (x), " xΠU, α>0.

При α = 2 получаем операцию концентрирование (уплотнение) CON(A) = A2. В рез. применения операции к множ. снижается степень нечеткости описания, причем для эл-тов с высокой степенью принадлежности это уменьшение относительно мало, а для эл-тов с малой степенью принадлежности относительно велико.

При α = 0.5 получаем операцию растяжения DIL(A)=0.5. Эта операция увеличивает степень нечеткости исходного нечеткого множества.

Операция контрастной интенсификации (INT) определяется с помощью функции принадлежности следующим образом:

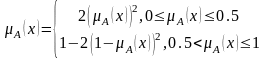
Пусть А₁, А₂, … А_n нечеткие подмножества универсумов U1, U2, … Un соответственно.

Прямое произведение А=А1 × А2 ×…× Аn явл. нечетким подмнож. декартового произведения U = U1 ×U2 ×…×Un c функцией принадлежности вида:

mA(x) = min(mA1(x1), …, mAn(xn)), x = (x1, …, xn) Î U

Нарушение законов (алгебры нечетких множеств?) при максимином и алгебраическом определении функции принадлежности.

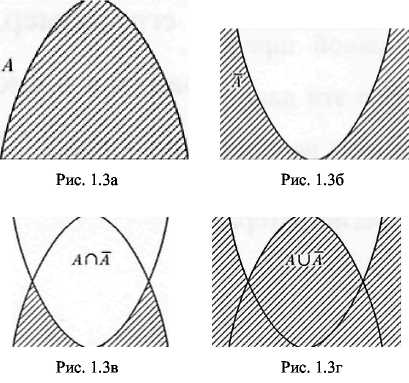
A ∩ -A ≠ Ø A È -A ≠ U

Нарушение законов (алгебры нечетких множеств?) при ограниченной функции принадлежности.

Идемпотентности: A Ç A≠A, A È A≠A.

Дистрибутивности: (A Ç B) È C ≠ (A Ç C) È (B Ç C)

(A È B) Ç C ≠ (A È C) Ç (B È C)