15

1. Множества. Отношение принадлежности. Способы задания множеств. Отношения включения и равенств множеств. Подмножество, надмножество, собственное подмножество. Универсум. Пустое множество. Мощность множества. Булеан множества. Семейство множеств.

«Множество — совокуп. предметов, кот. можно отличить друг от друга, и кот. представ. как единое целое. Предметы, кот. входят в состав множ., наз. его эл-тами».

• Через обознач. отношение принадлежности, т.е. означает, что эл-т принадлежит множ. .

• Если не явл. эл-том множ. A, то обознач. .

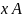• Два множ. A и B считаются равными, если они состоят из одних и тех же эл-тов. Пишется , если A и B равны, и в противном случае.

• Через обознач. отношение включения множеств, т.е. означает, что каждый эл-т множ. A явл. эл-том множ. B. В этом случае A наз. подмножеством B, а B — надмножеством A. Если и , то A наз. собственным подмножеством B, и в этом случае пишем .

• Мощность — кол-во эл-тов в множ.

• Пустое — множ., не содерж. эл-тов (мощность ), обознач. Æ.

• Универсум (универсальным множ.) — общее множ. для нескольких других, обознач. .

• Семейство — множ., все эл-ты кот. сами явл. множествами (множ. из множеств).

Теорема. Если мощность конеч. множ. А равна , то число всех подмножеств А равно 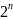, т. е. .

Булеан — множ. всех подмножеств множ. М, обознач. . Для конеч. множеств вып. .

Способы задания множеств:

• Перечисление эл-тов (если множ. конеч.);

#:

• Порождающая процедура (индуктивная, рекурсивная, комбинация из них);

# рекурсив.: ; ; .

• Описание хар-ристических св-в или хар-ристическим предикатом.

# хар-ристич. св-в:

2. Простое и необычное множество. Парадоксы и Антиномии. Парадокс Рассела и его роль в математике. Способы избежать Парадокса Рассела. Логические антиномии.

Антиномия — противоречие между 2 высказываниями, признаваемых одинаково верными.

Парадокс Рассела. Рассм. все множества, не содерж. самих себя. Рассм. множ. всех таких множеств. Тогда, если оно не содержит себя, то оно содержит себя.

Задание множеств хар-ристическим предикатом может привести к противоречиям. Рассм. множ. всех множеств, не содержащих себя в качестве эл-та: . Если такое множ. сущ., то можно определить, принадлежит ли оно само себе. С одной стороны, если , то . С другой стороны, если , то .

Это противоречие разрешается различ. способами, обычно сводящимся к тому, что не явл. множ.

Для 3-x множеств А, В, С справедливы соотнош.: ; ; ; .

Связь между включением и равенством множеств устанавливается следующим соотнош.: множества равны когда они явл. подмножествами друг друга. .

3. Операции над множествами и законы алгебры множеств. Диаграммы Эйлера. Формула включений и исключений. Покрытия и разбиения. Классы разбиения.

• Объединением (дизъюнкцией) 2-х множеств наз. множ. .

• Пересечением (конъюнкцией) 2-х множеств наз. множ. .

• Разностью 2-х множеств наз. множ. .

• Дополнением множ. A наз. разность , обознач. .

• Симметрической разностью 2-х множеств наз. множ., эл-ты которого принадлежат только 1 из множеств: .

Диаграмма Эйлера–Вэйна — геометрич. изображ. множеств на плоскости в виде областей.

• Покрытие множ. A — совокуп. множеств , кот. представ. собой их объединение.

• Разбиение множ. A — совокуп. , что совокуп. подмножеств покрытия A , при . Подмножества — классы разбиения.

Законы алгебры множеств:

1. Ассоц.: ; .

2. Коммут.: ; .

3. Иденп.: ; .

4. Дист. относ. слева и справа: ; .

5. Дист. относ. слева и справа: ; .

6. Св-ва дополнения: ; .

7. З-ны де Моргана: ; .

8. Св-ва универсума: ; .

9. З-ны пустого множ.: ; .

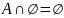10. Инволютивность: .

Формула включений и исключений:

.

4. Упорядоченная пара, кортеж, декартово произведение множеств. Прямое произведение n множеств, степень множества. Двуместное и n-местное соответствие. Способы задания соответствий. Пустое и полное соответствие.

Упорядоч. пара — запись вида (a, b), где , .

Кортеж — запись , где , …, .

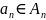Декартово (прямое) произведение 2 множеств — множ. всех упорядоч. пар эл-тов этих множеств:

.

#: , , .

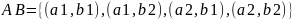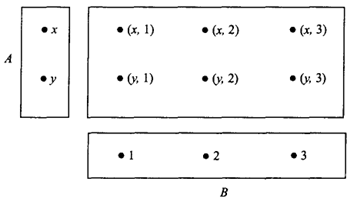
Декартово произведение n множеств — множ. кортежей, образованное эл-тами этих множ. — множ. .

Если 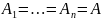, то .

Соответствие (бинарное отнош. м/ду множ. — 2–местное соотв.) произвольное подмнож. R из декартова произвед. этих множеств. (n множ. — n-местное соотв.)

Если , , то 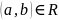( или ). Пустое соотв. — если 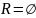, полное — если .

Способы задания соответствий: множ. кортежей; матрицей; сечением (фактор–множ.); диаграммой.

• Задание соответствия множ. картежей.

Поскольку соотв. явл. подмнож. декартового произвед., то его можно задать как перечислением (в т. ч. списком) конеч. числа картежей, так и их описанием.

#: Пусть .

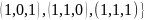. Мощность: .

• Матричное задание соответствий.

#: , .

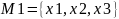	y1	y2
x1	1	1
x2	0	0
x3	1	0

• Задание соответствия сечением.

Множ. всех сечений эл-тов множ. наз. фактор-множ.

#: Пусть .

.

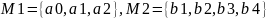• Диаграммное задание соответствий.

Обычно для соотв-вий диаграммным представлением явл. двудольный граф (доли — множества вершин, помеч. символами эл-тов множеств), или графич. представление соотв., а для отношений — псевдограф.

5. Область определения (прообраз Dom) и область значений (образ Im) соответствия. Образ (im) и прообраз (coim) элемента. Всюду определенное, сюръективное, функциональное и инъективное соответствие. Отображения множества А в (на) множество В, биективное и взаимнооднозначное соответствие. N-арная функция.

.

Область определения (прообраз, DomR) соотв. R — множ. эл-тов , для каждого из кот. найдется хотя бы 1 эл-т такой, что .

Область значений (образ, ImR) соотв. R наз. множ. эл-тов , для каждого из кот. найдется хотя бы 1 эл-т 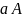такой, что .

Образ относительно R ( ) — множ. эл-тов таких, что .

Прообраз относительно ( 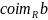) — множ. эл-тов таких, что .

; .

• Полностью определенное — соотв., у кот. каждый эл-т множ. А включен в соотв. ( ). В противном случае — частичное (частич. опред.).

• Сюръективное — соотв., у кот. каждый эл-т множ B включен в соотв. ( ).

• Функциональное — соотв., в кот., если эл-т имеет прообраз при соотв. R, то он единственный ( ).

• Инъективное — соотв., в кот., если эл-т , имеет прообраз при соотв. R, то он единственный ( ).

• Отображение (функция) из A в B ( ) — функциональное и полностью определенное соотв. Частичное отображение (частичная функция), если соотв. функц. и частич. Число n (кол-во эл-тов в отображ.) — арность отображ. соответствия.

• Отображение A на B ( ) — всюду опред., сюръектив. и функц. соотв.

• Биектив. — сюръектив. и инъектив. соотв.

• Взаимно однознач. — всюду опред., сюръектив., функц. и инъектив. соотв.