- •1.Предметы и задачи курса с.М.Классификация элементов конструкций
- •2.Допущения и гипотезы см
- •5.Деформации простые деформации
- •12. Хрупкие материалы
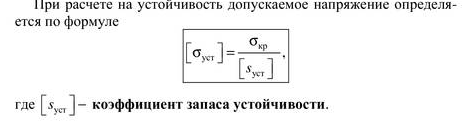
- •13.Допускаемое напряжение
- •14.Сдивг закон парности
- •15.Геометрические характеристики плоских сечений. Главные и центральные оси симметрии
- •16.Кручение Определение деформаций и напряжений
- •17.Расчёт на прочность и жёсткость при кручении
- •18.Изгиб.Виды изгиба.
- •19.Касательные напряжения при изгибе .Формула Журавского
- •20.Расчёты на прочность при изгибе
- •23.Напряжения в наклонных сечениях
- •24.Главные площадки
- •25. Площадки сдвига. Максимальное касательное напряжение.
- •27.Обобщённый закон гука
- •28.Теории прочности Теории прочности
- •Третья теория прочности
- •Четвертая теория прочности
- •29.Сложное сопротивление.Косой Изгиб.
- •31. Внецентренное сжатие
- •32.Кручение с изгибом Кручение с изгибом
- •33.Устойчивость сжатых стержней. Формула Ейлера
- •34 Пределы применимости формулы Ейлера
32.Кручение с изгибом Кручение с изгибом
Вид нагружения, при котором брус подвергается одновременно действию скручивающих и изгибающих моментов, называется изгибом с кручением.
При расчете воспользуемся принципом независимости действия сил. Определим напряжения по отдельности при изгибе и кручении.
При изгибе в поперечном сечении возникают нормальные напряжения, достигающие максимального значения в крайних волокнах
![]() .
.
При кручении в поперечном сечении возникают касательные напряжения, достигающие наибольшего значения в точках сечения у поверхности вала
![]() .
.
Условие прочности по третьей гипотезе прочности (гипотезе наибольших касательных напряжений)
![]() .
.
Учитывая,
что ![]() ,
, ![]() ,
получим условие прочности вала
,
получим условие прочности вала
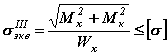 .
.
Если изгиб вала происходит в двух плоскостях, то условие прочности будет
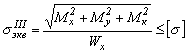 .
.
Используя четвертую (энергетическую) гипотезу прочности
![]() ,
,
после подстановки и получим
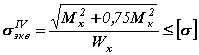 .
.
33.Устойчивость сжатых стержней. Формула Ейлера


34 Пределы применимости формулы Ейлера
Изучение
числовых величин, получаемых по формуле
Эйлера, показывает, что она дает правильные
результаты лишь в известных
пределах.Зависимость величины критических
напряжений, вычисленных при различных
значениях гибкости для стали представляется
гиперболической кривой, так называемой
«гиперболой Эйлеpa»: ![]() .
При помощи этой кривой мы узанём, что
представляемая ею формула
.
При помощи этой кривой мы узанём, что
представляемая ею формула ![]() получена
при помощи интегрирования дифференциального
уравнения изогнутой оси, т. е. в
предположении, что
напряжения в стержне в момент потери
устойчивости не превосходят предела
пропорциональности.
получена
при помощи интегрирования дифференциального
уравнения изогнутой оси, т. е. в
предположении, что
напряжения в стержне в момент потери
устойчивости не превосходят предела
пропорциональности.
Следовательно,
мы не имеем права пользоваться величинами
критических напряжений, вычисленных
по формуле Эйлера, если они получаются
выше этого предела для данного материала.
Иначе говоря, формула Эйлера применима
лишь при соблюдении условия:
![]() или
или ![]()
Если
из этого неравенства выразить гибкость ![]() ,
то условие применимости формул Эйлера
получит иной вид:
,
то условие применимости формул Эйлера
получит иной вид:
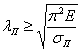
35.Расчёт на устойчивость