Задача №3

Проведено 6-процентное обследование качества поступившей партии товара. На основе механического способа отбора в выборочную совокупность взято 900 единиц, из которых 48 оказались бракованными. Средний вес одного изделия в выборке составил 10,8 кг, а среднее квадратическое отклонение - 0,35.

Определите:

1. С вероятностью 0,954 пределы, в которых находится генеральная доля бракованной продукции.

2. С вероятностью 0,997 пределы, в которых находится средний вес одного изделия во всей партии товара.

Решение:

1. Установим характеристики выборочной совокупности.

Выборочная доля или частность w определяется из отношения единиц обладающих изучаемым признаком m, к общей численности единиц выборочной совокупности n:

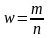
Поскольку из 900 единиц, попавших в выборку n, 48 оказались бракованными ед., то показатель частости (95%).

Средний вес одного изделия в выборке кг. определен взвешиванием. Но полученные показатели частости (0,94) и средней величины (10,8 кг.) характеризуют долю набракованной продукции и средний вес одного изделия лишь в выборке. Для определения соответствующих показателей для всей партии товара надо установить возможные при этом значения ошибки выборки.

При определении границ генеральной доли при расчете средней ошибки выборки используется дисперсия альтернативного признака, которая вычисляется по формуле:

– доля единиц не обладающих данным признаком в выборке (бракованные изделия)

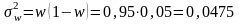
Определим предельную ошибку выборки, она связана с заданным уровнем вероятности. В условии задачи требуемая вероятность составляет 0,954 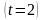и 0,957 . С учетом выбранного уровня вероятности и соответствующего ему значения t предельная ошибка выборки составит:

,

где 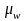– средняя ошибка выборки

,

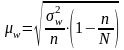где N – объем (число единиц) генеральной совокупности.

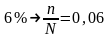
Определим предельную ошибку выборки:

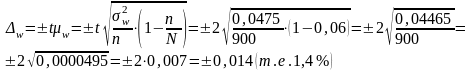
При заданной вероятности генеральная доля 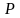находится в следующих границах:

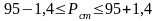
– для стандартной продукции

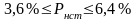– для нестандартной (бракованной) продукции

Вывод: С вероятностью 0,954 можно утверждать, что генеральная доля бракованной продукции находится в пределах от 3,6 до 6,4 % во всей партии товара.

2. Средний вес одного изделия в выборке кг.

Среднее квадратическое отклонение

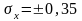
Найдем дисперсию количественного признака:

Предельная ошибка выборки для количественного признака находится по формуле:

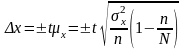
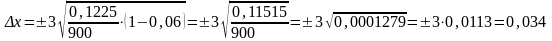кг.

При заданной вероятности генеральная средняя 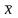будет находиться в следующих границах:

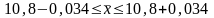
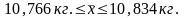
Вывод: С вероятностью 0,997 можно утверждать, что средний вес одного изделия в пределах товара будет равен от 10,766 до 10,834 кг.

Задача №4

Имеются следующие данные о продаже тканей торговой организацией (в сопоставимых ценах) в 1994 – 1998 г.г.:

Годы	1994	1995	1996	1997	1998
Продажа тканей, (млн. руб.)	1,46	2.32	2,18	2,45	2,81

На основе приведённых данных:

1. Для анализа ряда динамики определите:

   1. абсолютные приросты, темпы роста и темпы прироста (цепные и базисные);

   2. средние: абсолютный прирост и темпы прироста.

Для характеристики интенсивности динамики постройте соответствующий график.

2. Для анализа общей тенденции продажи тканей методом аналитического выравнивания:

   1. вычислите теоретические (выровненные) уровни и нанесите их на график, сравнив с фактическими;

   2. методом экстраполяции тренда рассчитайте прогноз на 1999 г.

Сделайте выводы.

Решение:

1.1 Рассчитаем основные показатели динамики продаж ткани торговой организацией в 1994 – 1998 г.г. Полученные результаты занесем в табл. № 4.1

Из таблицы видно, что по сравнению с 1994 г. в каждом последующем году за исключением 1996 г. происходило систематическое увеличение абсолютных приростов (млн. руб.) продажи ткани 0,86>0,72<0,99<1,35. Абсолютное уменьшение продажи ткани за 1996 г. по сравнению с 1995 г. составило – 0,14 млн. руб.

Между базисными и цепными абсолютными приростами есть связь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики :

.

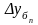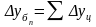млн. руб.

Показатели базисных темпов роста свидетельствуют, что по сравнению с 1994 г. происходило увеличение продаж ткани, т.к. показатели темпов роста больше 100%. В результате темп роста в 1998 г. достиг 192,47% базисного уровня.

Таблица 4.1 Расчеты основных показателей динамики продаж ткани торговой организацией в 1994 – 1998 г.г.

Показатель	1994	1995	1996	1997	1998
Продажа ткани, млн. руб., y	1,46	2,32	2,18	2,45	2,81
Абсолютный прирост, млн. руб.
базисный	–
цепной	–
Темп роста, %
базисный	–
цепной	–
Темп прироста, %
базисный	–
цепной	–

Цепные темпы роста в 1998 г. достигли 192,47% базисного уровня. Цепные темпы роста показывают, что имело место замедление погодовых темпов (%) в 1996 г. по сравнению с 1995 г. (158,9>93,97.) В последующих 1997, 1998 гг. наблюдалось увеличение погодовых темпов по сравнению с 1996 г. (93,97>112.39>114.69).

Между базисными и цепными темпами роста есть взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:

.

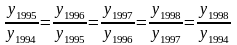Подставим вычисленные в таблице цепные темпы роста (в коэффициентах):

,

получаем базисный темп роста в 1998 г.=1,9247.

Между показателями темпа прироста и темпами роста имеется взаимосвязь:

.

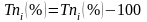Так, на основе вычисленного для 1998 г. базисного темпа роста продаж 192,47% можно определить темп прироста:

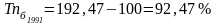
В 1996 г. цепной темп роста составил 93,97% по сравнению с 1995 г., следовательно цепной темп прироста в 1996 г. будет равен:

,

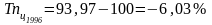т.е. произошло сокращение продаж на 6,03%.

В 1997, 1998 гг. наблюдалось увеличение темпа прироста продаж. Максимальный прирост был в 1998 г. и составил 92,47% по сравнению с базисным 1994 г.

1.2 На основе полученных данных по абсолютным приростам, темпам роста и темпам прироста (цепным и базисным) создадим таблицу динамики продажи ткани торговой организацией в 1994 – 1998 гг. и вычислим средние показатели: абсолютный прирост и темпы прироста.

Таблица 4.2 Динамика продажи ткани торговой организацией в 1994 – 1998 гг. и расчет аналитических показателей динамики.

Год	Объем продаж ткани (млн.руб)	Абсолютные приросты (снижение) (млн.руб)			Коэффициент роста			Темпы роста %			Темпы прироста %
		цепной	базисный	цепной		базисный	цепной		базисный	цепной		базисный
А	1	2	3	4		5	6		7	8		9
1994	1,46	–	–	–		–	–		–	–		–
1995	2,32	0,86	0,86	1,589		1,589	158,9		158,9	58,9		58,9
1996	2,18	–0,14	0,72	0,937		1,4931	93,7		149,32	–6,03		49,32
1997	2,45	0,27	0,99	1,1239		1,6781	112,39		167,81	12,39		67,81
1998	2,81	0,36	1,35	1,1469		1,9247	114,69		192,47	14,69		92,47
В сред-нем

Для получения обобщающих показателей динамики продаж ткани в 1994–1998 гг. определим средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста.

В интервальных рядах динамики средний уровень определяется делением суммы уровней на число уровней п:

млн. руб.

Для определения среднего абсолютного прироста 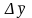, сумма цепных абсолютных приростов 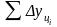делится на число приростов п:

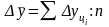
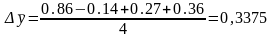млн. руб.

Средний абсолютный прирост можно определить по абсолютным уровням ряда динамики. Для этого определяется разность между конечным и базисным 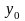уровнями наблюдаемого периода, которая делится на 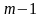субпериодов.

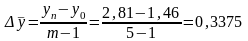млн. руб.

Таким образом, в среднем за исследуемый период ежегодное увеличение продажи тканей составило 0,3375 млн. руб.

Для определения среднего темпа роста – обобщающей характеристики индивидуальных темпов роста ряда динамики, применяется формула:

,

где 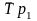, , 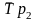…, 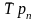– индивидуальные (цепные) темпы роста (в коэффициентах);

n – число индивидуальных темпов роста.

или 117,8%

Средний темп роста можно определить и по абсолютным уровням ряда динамики по формуле:

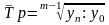
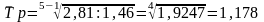или 117,8%

На основе взаимосвязи между цепными и базисными темпами роста, средний темп роста можно определить по формуле:

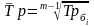
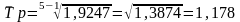или 117,8%.

В результате, среднее относительное увеличение реализации тканей за 1994-1998 гг. составило 17,8 % в год.

Средний темп прироста –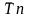 можно определить на основе взаимосвязи между темпами роста и прироста. при наличии данных о средних темпах роста для получения средних темпов прироста используется зависимость:

(при выражении среднего темпа роста в коэффициентах).

Применяя данную формулу, можно вычислить средний темп прироста объема продаж ткани торговой организацией в 1994–1998 гг. на основе среднего темпа роста как :

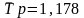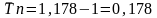, или 17,7%

Для характеристики интенсивности динамики построим график продаж ткани.

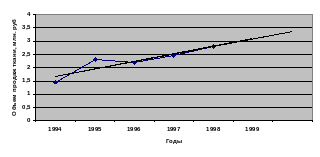
▪––––––––▪ фактические уровни

теоретические уровни

Рис. 2. Фактические и теоретические значения продаж ткани в 1994-1998 гг. и прогнозирование продаж на 1999 г.

2.1 Из характера размещения уровней анализируемого ряда динамики на поле графика можно сделать предположение, что при применении тренда при аналитическом изучении ряда это может быть уравнение прямолинейной функции.

Таблица 4.3 Исходные расчетные данные для определения параметров системы уравнения

Год	Объем продаж млн. руб.
1994	1,46	–2	4	–2,92	1,679	–0,219	0,0479
1995	2,32	–1	1	–2,32	1,961	0,359	0,1289
1996	2,18	0	0	0	2,244	–0,064	0,0041
1997	2,45	1	1	2,45	2,527	–0,077	0,0059
1998	2,81	2	4	5,62	2,81	0	0
Итого	11,22	–	10	2,83	11,22	–	0,1868

Для выравнивания ряда динамики по прямой используем уравнение .

Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров 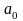и :

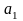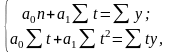
где у – исходный уровень ряда динамики;

п –число членов ряда;

t – показатель времени, который обозначается порядковыми номерами, начиная от низшего.

Решение системы уравнений позволяет получить выражения для параметров и :

Для упрощения техники расчета параметров уравнения, показателям времени t придадим такие значения, чтобы их сумма была равна нулю, т.е. 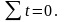Число исходных уровней ряда нечетное 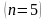. При этом уравнения системы примут вид:

и

откуда: 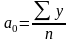представляет собой средний уровень ряда динамики ;

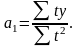
По итоговым данным приведенным в таблице 4.3 определим параметры уравнения:

;

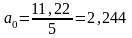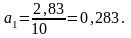
В результате получаем трендовую модель следующее уравнение основной тенденции продаж ткани торговой организацией в 1994–1998 гг.:

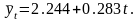
Параметр трендовой модели показывает, что объем продаж ткани, возрастает в среднем на 0,283 млн. руб. в год.

Подставляя в уравнение принятые обозначения t, вычислим выравненные теоритические уровни ряда динамики:

1994 г. –

1995 г. –

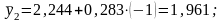
1996 г. –

1997 г. –

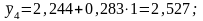
1998 г. –

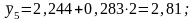
Сумма теоретических уровней ряда динамики будет равна сумме фактических:

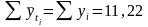
Рассчитаем показатель колеблемости продаж ткани с помощью формулы среднего квадратического отклонения:

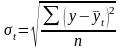
млн. руб.

Относительной мерой колеблемости является коэффициент вариации, который вычисляется по формуле:

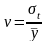
, или 21,71%.

Перенесем теоретические уровни на график.

2.2. При прогнозировании тренда изучаемого явления на основе аналитического выравнивания для экстраполяции тренда применяется адекватная трендовая модель. Так при выравнивании продаж ткани торговой организацией в 1994–1998 гг. была определена на основе прямолинейной функции трендовая модель:

Для прогнозирования возможного развития продаж в 1999 г. в модель подставляется t = 3

млн. руб.

Перенесем данный прогноз на график.

Таким образом, возможный уровень продаж ткани торговой организацией в 1999 г. составит 3,093 млн. руб.