11. Основные законы геометрической оптики
Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Опытным доказательством этого закона могут служить резкие тени, отбрасываемые непрозрачными телами при освещении светом источника достаточно малых размеров («точечный источник»). Таким образом, геометрическая оптика, опирающаяся на представление о световых лучах, есть предельный случай волновой оптики приλ → 0. Границы применимости геометрической оптики будут рассмотрены в разделе о дифракции света.
Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α.
Закон преломления света: падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред:
|
Постоянную величину n называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.
Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления:
n = n2 / n1. |
12. Тонкая линза. Построение изображений.
Тонкая линза — линза, когда толщина самой линзы d (расстояние между наружныим точками сфер) мала по сравнению с радиусами кривизны сферических поверхностей d <<R1 и R2. В противном случае такие линзы называются толстыми. Расстояния от точки предмета до центра линзы и от точки изображения до центра линзы называются сопряжёнными фокусными расстояниями
формула тонкой линзы:
1u+1v=1f
где u — расстояние от линзы до предмета; v — расстояние от линзы до изображения; f — главное фокусное расстояние линзы. В случае толстой линзы формула остаётся без изменения с той лишь разницей, что расстояния отсчитываются не от центра линзы, а от главных плоскостей.
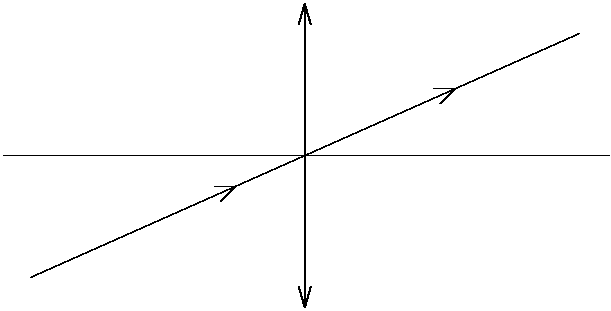
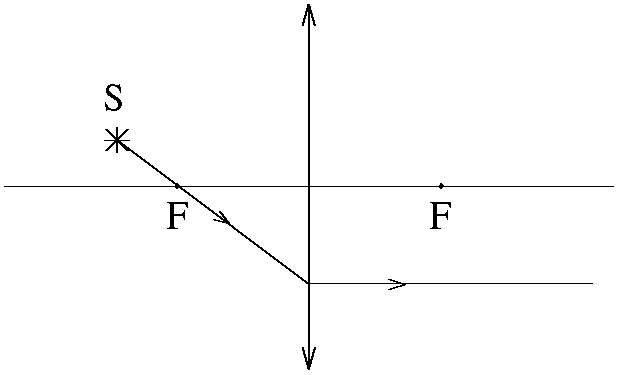
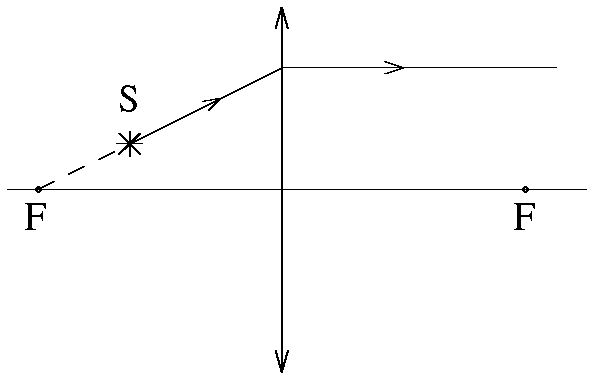
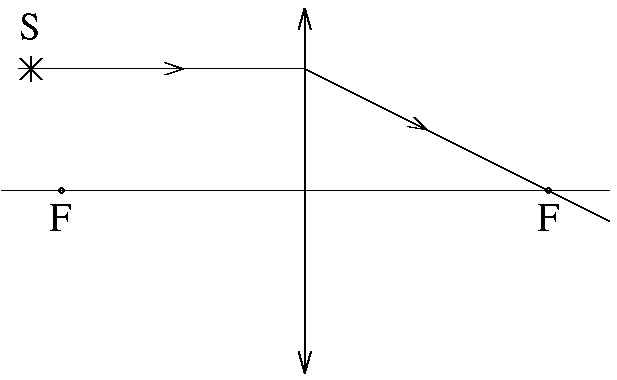
Построение изображения в тонкой линзе Есть три луча, удобных для построения изображения точечного источника света в тонкой линзе. Первый луч проходит через центр линзы. После линзы он не изменяет своего направления (рис. 7,а) как для собирающей так и для рассеивающей линзы. Это справедливо только в том случае, если среда с обеих сторон линзы имеет одинаковый показатель преломления. Два других удобных луча рассмотрим на примере собирающей линзы. Один из них проходит через передний фокус (рис. 7,б), или его продолжение назад проходит через передний фокус (рис. 7,в). После линзы такой луч пойдет параллельно оптической оси. Другой луч проходит до линзы параллельно оптической оси, а после линзы через задний фокус (рис. 7,г).
13. Интерференция света. Интерференционная картина от двух щелей.
Интерференция – одно из ярких проявлений волновой природы света. Это интересное и красивое явление наблюдается при наложении двух или нескольких световых пучков. Интенсивность света в области перекрывания пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра.
Расчет интерференционной картины может быть очень упрощенный, если рассматривать не точечные, а линейные источники - узкие, параллельные и близко расположенные щели. Две щели А и В, расположенные перпендикулярно к плоскости чертежа на расстоянии друг от друга, и являются когерентными источниками света.
Экран Е также перпендикулярно плоскости рисунка и параллельный обеим щелям. Рассчитывается разность хода лучей для произвольной точки М, расположенной на расстоянии x от центральной линии экрана. Экран находится на расстоянии l от щели, которая намного больше расстояния d между щелями. Имеем:
l22 = l2 + ( x + d/2)2 l12 = l2 + ( x – d/2)2 , отнимая друг от друга уравнения, получим
( l2 – l1) (l2 + l1) = 2xd. Из условия l>>d следует, что l2 + l1 » 2l. Позначившы искомую разность хода l2 –l1= D, получим: D » 2xd/2l » xd/l (11). В тех местах на экране, где эта разность хода равна целому числу волн или парном числу полуволн:
Dmax = 2ml/2, (m = 0,±1,±2,±3,…) (12)
колебания, которые приходят от обоих источников, прилагаемых поэтому амплитуда удваивается, а интенсивность возрастает в 4 раза. В тех местах экрана, где разность хода равна нечетному числу полуволн:
Dmin = (2m + 1)l/2, (m = 0,±1,±2,±3,…), (13)
волны от обоих источников приходят в противофазе и полностью гасят друг друга.
В результате этого на экране будет наблюдаться система светлых и темных полос, чередующихся с постепенными переходами. Из формул (11) и (12) находим положение последовательных максимумов:
Xmax = mll/d. (14)
Расстояние между соседними максимумами - расстояние между интерференционными полосами - остается неизменной вдоль экрана и равна:
Dх = xm+1 – xm = (m+1)ll/d - mll/d = ll/d. (15)