
- •18) Уравнение плоскости в пространстве
- •1 9) Уравнение прямой в пространстве.
- •20) Пространства Cn и Rn. Линейная зависимость и независимость векторов.
- •2.1.3. Необходимое и достаточное условие линейной зависимости системы векторов
- •2.1.4. Необходимое условие линейной независимости системы векторов (в координатах)
- •23)Норма векторов в Cn и Rn.
- •24)Ортогональность векторов. Ортогональные и ортонормированный базисы.
- •25) Разложение векторов по ортогональному (ортонормированному) базису. Коэффициенты Фурье.
- •28) Квадратичные формы. Приведение к каноническому виду. Классификация квадратичных форм.
АиГ
К

 омплексные
числа, алгебраическая форма записи,
арифметические операции.
омплексные
числа, алгебраическая форма записи,
арифметические операции.


Геометрическое представление комплексных чисел. Модуль, аргумент, тригонометрическая форма записи.


Модуль и аргумент произведения и частного. Формула Муавра. Экспоненциальная форма записи комплексных чисел



М
 атрицы.
Линейные операции над матрицами.
атрицы.
Линейные операции над матрицами.

Матрицы. Умножение матриц.


Системы линейных уравнений. Матричная запись. Допустимые преобразования.


у
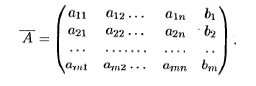
М
 етод
Гаусса-Жордана решения систем линейных
уравнений.
етод
Гаусса-Жордана решения систем линейных
уравнений.



Определитель квадратной матрицы. Свойства (разложение по столбцам и строкам, перестановка строк и столбцов)
Свойства (Линейность по столбцам и строкам)
Свойства (Определитель транспонированной матрицы. Определитель произведения матриц.)





11) Теорема Крамера. Формулы Крамера.

12) Обратная теорема Крамера
Если система линейных уравнений с квадратной матрицей имеет единственное решение, то определитель этой матрицы не равен нулю.
Доказательство: По скольку система имеет единственное решение, алгоритм Гаусса-Жордана заканчивается получением системы с единичной матрицей, определитель которой не равен 0. Предположим, что в исходной системе det(А)=0, но тогда после каждого шага алгоритма мы должны получать систему с матрицей, определитель которой так же равен 0. Полученное противоречие и доказывает теорему.
1 3)
Однородные системы линейных уравнений
3)
Однородные системы линейных уравнений
1 4)
Матричные уравнения AX=B
и XA=B
4)
Матричные уравнения AX=B
и XA=B



15) Обратная матрица. Условия существования и единственности. Способ нахождения.
16) Обратная матрица. Формулы для её элементов.



![]()
17) Векторное пространство R3. Скалярное произведение векторов.
R3 - это трехмерное пространство; при этом имеем
![]()



18) Уравнение плоскости в пространстве



1 9) Уравнение прямой в пространстве.
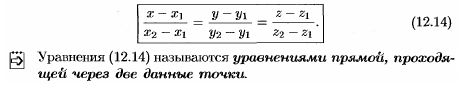
20) Пространства Cn и Rn. Линейная зависимость и независимость векторов.
Rn — координатное n-мерное пространство с полем скаляров R.
Cn — комплексное координатное n-мерное пространство над полем C комплексных чисел.
Линейная зависимость и линейная независимость в Rn
Говорят,
что вектор ![]() пространства Rn линейно
выражается через
векторы
пространства Rn линейно
выражается через
векторы ![]() ,
если его можно представить в виде линейной
комбинации этих
элементов
,
если его можно представить в виде линейной
комбинации этих
элементов ![]() ,
т.е. представить в виде
,
т.е. представить в виде ![]() .
.
Определение. Если
хотя бы один вектор системы векторов ![]() из
Rn линейно
выражается через остальные векторы
системы, то система векторов называется
линейно зависимой.
из
Rn линейно
выражается через остальные векторы
системы, то система векторов называется
линейно зависимой.
Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.
2.1.3. Необходимое и достаточное условие линейной зависимости системы векторов
Справедливо следующее утверждение.
Теорема. Система
векторов
из Rn линейно
зависима тогда и только тогда, когда
хотя бы один вектор системы векторов
из
Rn линейно
выражается через остальные векторы
системы.![]()
Это утверждение (необходимое и достаточное условие линейной зависимости) доказано на лекции.
Н етрудно
доказать, что система арифметических
векторов
етрудно
доказать, что система арифметических
векторов
линейно
независима и что для любого ![]() из Rn система
векторов
из Rn система
векторов ![]() линейно
зависима:
линейно
зависима: ![]() .
.
2.1.4. Необходимое условие линейной независимости системы векторов (в координатах)
Теорема
(необходимое и достаточное условие
линейной независимости в координатной
форме). Cистема
векторов ![]() из
Rn линейно
независима тогда и только тогда, когда
отличен от нуля определитель, строками
(столбцами) которого являются компоненты
векторов системы:
из
Rn линейно
независима тогда и только тогда, когда
отличен от нуля определитель, строками
(столбцами) которого являются компоненты
векторов системы:
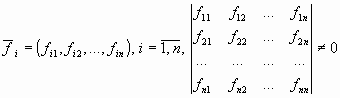
Следствиями из этой теоремы являются следующие утверждения:
1. если
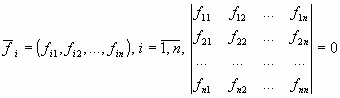 ,
то система векторов
из
Rn —
линейно зависима;
,
то система векторов
из
Rn —
линейно зависима;любая система векторов
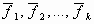 из
Rn, k
> n —
линейно зависима.
из
Rn, k
> n —
линейно зависима.
23)Норма векторов в Cn и Rn.
Определение(
для Cn)
Пусть каждому вектору
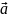 из Cn
поставлено в соответствие вещественное
неотрицательное число ||
||.
Оно называется нормой вектора
,
если выполняет следующие три условия(аксиомы
нормы):
из Cn
поставлено в соответствие вещественное
неотрицательное число ||
||.
Оно называется нормой вектора
,
если выполняет следующие три условия(аксиомы
нормы):
Норма
вектора равна
нулю тогда и только тогда, когда
=

||
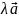 ||=
|λ|*||
||
||=
|λ|*||
||Неравенство треугольника
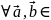 Cn
Cn||
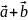 ||
= ||
||
= || ||
+ ||
||
+ || ||
||
Пример:
Евклидова норма: ||
||=
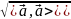 =
=
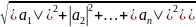
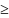 0
0
Ясно,
что ||
||=0
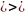 =
1
аксиома выполнена
=
1
аксиома выполнена
||
||=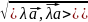 =
=
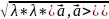 =
=
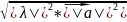 = |λ|*||
||
2 аксиома
выполнена
= |λ|*||
||
2 аксиома
выполнена
Справедливость 3-й аксиомы для Евклидовой нормы следует из неравенства Каши-Буняковского для скалярного произведения
Пример: || || = max {|a1|, |a2|, |a3|, … |an|}
Пример: || ||= |a1|, |a2|, |a3|, … |an|
