Проверка ряда на однородность.

Для проверки однородности гидрологических рядов, используются критерии двух типов: параметрический и непараметрический. В данном задании будут рассмотрены параметрические критерии Стьюдента и Фишера. Критерием Стьюдента проверяем ряд на однородность по среднему значению, а критерием Фишера – по дисперсии.

Критерии Фишера и Стьюдента относятся к категории стандартных критериев и рекомендуются в большинстве нормативных документов в качестве официального теста на однородность.

Для этого исходный ряд разбивается на две приблизительно равные части и для каждой из частей рассчитывается среднее значение, среднеквадратическое отклонение и дисперсия. Полученные значения заносим в таблицу 2.

Проверка ряда на однородность
Выборка	Длина выборки	Сренее значение,Qм3/с	СКО, σ	дисперсия, D	Xi-Xср	(Xi-Xср)^2
1 часть ряда	9	6,31	72,31	5229,37	-99,48	9896
		6,75			-99,04	9809
		5,84			-99,95	9990
		5,59			-100,20	10040
		6,95			-98,84	9769
		6,28		Ср.знач1	-99,51	9902
		8		6,41	-97,79	9563
		3,6		Сумма1	-102,19	10443
		8,39		88899,26	-97,40	9487
2 часть ряда	9	5,46	73,09	5342,09	-100,33	10066
		6,16			-99,63	9926
		6,14			-99,65	9930
		6,41			-99,38	9876
		3,67			-102,12	10428
		6,16			-99,63	9926
		4,18			-101,61	10325
		5,28			-100,51	10102
		4,62		Ср.знач2	-101,17	10235
Весь ряд	18	105,79		5,34	Cумма2	90816
		Гипотеза об однородности ряда по критерию Фишера при уровне значимости 2α=5% не опровергается
F*	0,98
Fт	4,43
S	72,70	Гипотеза об однородности ряда по критерию Стьюдента при уровне значимости 2α=5% не опровергается
t*	0,07
tT	2,110

1) Проверка ряда на однородность по дисперсии (критерий Фишера)

Рассчитываем эмпирическое значение критерия Фишера:

F*=D1/D2 (1)

Полученное значение F*сравниваем с табличным значением Fт.

Так как при принятом уровне значимости выполняется неравенство F*<Fт, то можно считать различие в дисперсиях по отдельным частям ряда незначительным. В этом случае говорят, что гипотеза об однородности ряда по критерию Фишера при уровне значимости 2α=5% не опровергаются.

2) Выборки Х и Y длиной ряда mи nиз нормальных распределений с неизвестными параметрами m_x, σ_x, и n_y, σ_y, но при этом известно, что σ_x=σ_y, т.е. они имеют одинаковое, хотя и неизвестное СКО, которое обозначим буквой σ (без индекса):

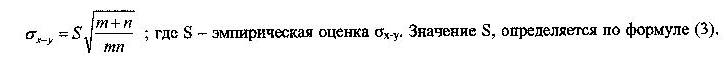
В окончательном виде выражение для статистики t имеет вид: (формула 2).

Проверка ряда на однородность по среднему значению (критерий Стьюдента) при уровне значимости 2α=5%.

Рассчитываем эмпирическое значение критерия Стьюдента.

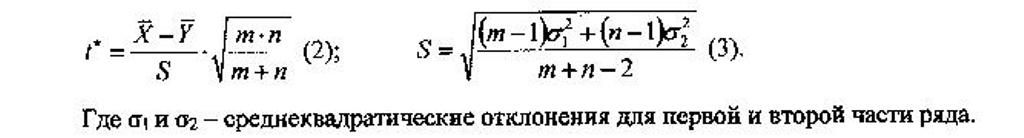
Находим табличное значение t_T=2,12 Полученное эмпирическое значение t* сравниваем с табличным значением tт.

Так как при принятом уровне значимости выполняется неравенство t*<tт, то можно считать различие в средних значениях по отдельным частям ряда не значительным. В этом случае говорят, что гипотеза об однородности ряда по критерию Стьюдента при уровне значимости 2α=5% не опровергается. Таким образом, считаем ряд однородным по критерию Фишера и по критерию Стьюдента.