26. Проверка ряда на однородность, её цель и методы определения.

Анализ на однородность

Оценку однородности рядов гидрологических наблюдений осуществляют на основе генетического и статистического анализов исходных данных наблюдений. Генетический анализ условий формирования речного стока заключается в выявлении физических причин, обусловливающих неоднородность исходных данных наблюдений [113]. Для количественной оценки статистической однородности могут использоваться критерии двух типов: параметрические и непараметрические.

В параметрических критериях при вычислении статистики используются выборочные оценки параметров распределения. При этом считается, что исходная выборка относится к генеральной совокупности с известным типом распределения. Непараметрические критерии базируются на использовании непараметрических статистик, то есть ее распределение не зависит от распределения анализируемых переменных. Необходимым условием применения критериев однородности является предварительная проверка случайности используемой информации, поскольку неучет внутрирядных связей может привести к тому, что однородные данные будут признаны неоднородными, а неучет корреляционных связей между рядами наблюдений, наоборот, к тому, что неоднородные данные будут отнесены к однородным [96]. На практике обычно применяют параметрические критерии (Фишера – для проверки однородности выборочных дисперсий; Стьюдента – для проверки однородности выборочных дисперсий) [113]. Из непараметрических критериев чаще всего используется критерий Уилкоксона.

Критерий Фишера (приводится по [66, 96]). Однородность двух выборок, состоящих из нормально распределенных случайных величин, можно проверить с помощью критерия Фишера:

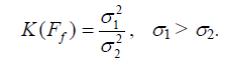. (3.3.3.1)

Величина K(Ff) подчиняется закону распределения Фишера. Если K(Ff) < K(Fα,υ1,υ2) (числа степеней свободы υ1 = N1 – 1, υ2 = N2 – 1; N1 и N2 – объемы сравниваемых выборок с соответствующими стандартными отклонениями σ1 и σ2), то гипотеза однородности дисперсий не отвергается.

Критерий Стьюдента Из множества параметрических критериев рассмотрим наиболее часто используемый критерий Стьюдента для случайных величин, распределенных по нормальному закону:

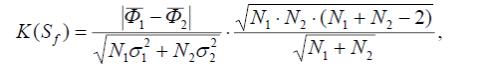, (3.3.3.2)

где 1 Ф и 2 Ф – средние значения для сравниваемых выборок. Если K(Sf) < K(Sα), то с заданным уровнем значимости принимается гипотеза 1 Ф = 2 Ф (число степеней свободы υ = N1 + N2 – 2, N1 ≥ 2, N2 ≥ 2). При распределении вероятностей, отличном от нормального, и наличии автокорреляции в критическое значение вводится поправка:

K(Sα)′ = kstK(Sα), (3.3.3.3) где kst – переходный коэффициент, определяемый согласно.

Критерий Уилкоксона (приводится по [96]). Из числа непараметрических критериев однородности средних широкое распространение получил критерий Уилкоксона, основанный на подсчете числа инверсий. Пусть имеется последовательность, составленная из 2-х выборок Ф1 и Ф2 объемом N1 и N2 соответственно: Ф2,1Ф1,1Ф1,2Ф2,2Ф2,3Ф2,4Ф1,3Ф2,5Ф2,6Ф1,4. Если какому-либо значению Ф1 предшествует некоторое значение Ф2, то говорят, что пара образует инверсию. Например, в рассматриваемой последовательности Ф1,1 и Ф1,2 образует по одной инверсии с Ф2,1, 1,3 образует 4 инверсии (с Ф2,1, Ф2,2, Ф2,3, Ф2,4), а Ф1,4 – 6 инверсий (с Ф2,1, Ф2,2, Ф2,3, Ф2,4, Ф2,5, Ф2,6), то есть всего 12 инверсий (K(uf) = 12). Если объем выборки не менее 10, то число инверсий приближенно подчиняется нормальному закону распределения с математическим ожиданием Mu = 0,5N1N2 и дисперсией D* u = (N1 + N2 + 1) N1N2 / 12. Границы критической области для нулевой гипотезы об однородности средних: K(uf) ≤ Mu – kn,ασu,k; K(uf) ≥ Mu + kn,ασu,k, (3.3.3.4)

где kn,α – квантиль нормального распределения; *u,k u σ = D . Если число инверсий K(uf) оказывается в критической области, то нулевая гипотеза о принадлежности сравниваемых выборок к одной генеральной совокупности отвергается (K(u5 %) = 1,65).