23. Статистические характеристики гидрометеорологических рядов написать зависимости по которым они определяются.

Событие, которое при наличии соответствующего комплекса условий может наступить или не наступить наз-ся случайным событием.

Различают:

-случайное событие

-случайная величина

Параметры распределения:

1. среднее многолетнее значение годового стока, как Q’=∑Qi/n , и может быть принято в качестве нормы годового стока, если его ошибка σ_Q0≤ 10%.

2. Коэффициент вариации определяется по формуле Cv=σ/ Q’=√∑((к-1)^2)/n-1

-это отношение изменчивости к среднеарифметическому значению

3. Коэффициент асимметрии по формуле

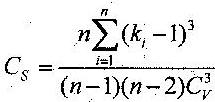
К –модульный коэффициент; Сs – показывает симметричность ряда

4. Среднеквадратическое отклонение рассчитывается по формуле

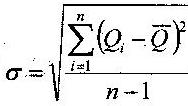
-это абсолютная характеристика изменчивости ряда (n-1, если длина ряда меньше 30лет)

1. Относительная погрешность параметров распределения определяется по формулам:

Ошибка нормы годового стока σ_Q0= 100%* Cv/ √n

Ошибка коэффициента вариации:

ECv= √(1+ Cv)*100% / √2n

Ошибка коэффициента асимметрии:

E_Cs = 1/ Cs*√(6/n)(1 + 6(Cv^2) + 5(Cv^4))*100%

2. Окончательное значение нормы с учетом ошибки указывается как:

Q₀ = Q ± δ, м³/с

δ= Q * σ_Q0 /100

25. Проверка ряда на случайность, её цель и методы определения.

Цель: выбор наиболее адекватной математической модели для описания вероятностной структуры гидрологического ряда.

Для проверки случайности исп-ся статист критерий:

Коэффициент автокорреляции

r<δ_rt_2a

δ= (1-r²)/(√n-2)

где t_2a – нормированная ордината нормального распределения; 2а – уровень значимости обычно 5% или 10%

Статистический анализ исходной информации

Корректное использование информации при проведении гидрологических расчетов предполагает ее обязательный анализ на случайность, однородность и согласие эмпирической и теоретической кривой распределения. Этот анализ включает следующие основные этапы: 1) формулировку нулевой и альтернативных гипотез; 2) определение уровня значимости и выбор критической области; 3) принятие решения. Формулировка гипотез осуществляется на основании результатов предварительно проведенного изического анализа информации и существующей физической теории рассматриваемого явления (например делается предположение о существовании неоднородности изучаемых рядов). Спецификой гидрологических расчетов является то, что в случае наличия данных наблюдений они сводятся к применению аналитических функций распределения ежегодных вероятностей превышения (кривых обеспеченностей). Таким образом, один из элементов статистического анализа – проверка на согласие эмпирической и теоретической

кривых распределения – одновременно является и одной из важнейших задач гидрологических расчетов.

Анализ на случайность

Проверка гипотезы случайности рассматриваемой величины или функции является неотъемлемым этапом статистического анализа. Сущность проверки заключается в выяснении вопроса, является ли изменение данной величины случайным или закономерным, связанным с каким-либо постоянно действующим физическим фактором. Для этого используются критерии, основанные на сравнении свойств исследуемого процесса со свойствами последовательности, в которой тренд заведомо отсутствует. Существует целый ряд подобных критериев, в том числе критерий Питмена.

Критерий Питмена (приводится по [122] для наиболее простого случая – линейного тренда). Пусть зависимость гидрологической характеристики Ф от времени t имеет вид:

Ф(t) = a·t+b+ξ, (3.3.2.1) где t – год; a, b – эмпирические константы; ξ – случайная величина. Гипотеза о неслучайном изменении Ф(t) принимается, если при заданном уровне значимости фактическое значение статистики K( τf), вычисленное по формулам (3.3.2.2, 3.3.2.3), больше критического значения.

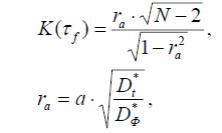
Ф – дисперсия временного ряда и максимальных годовых уровней соответственно. Критическое значение K(τα) находится как квантиль распределения Стьюдента при заданном уровне значимости и числе степеней свободы N–2.