Var count:integer);
Begin
if q<>nil { ограничитель рекурсии } then
begin
Inc(count);
Count_El( q^.next , count);
end
End;
При входе в процедуру count = 0 ,а q=first (указатель на первый элемент списка). Далее рекурсивная процедура работает так. Анализируется значение указателя, переданного в процедуру. Если он не равен Nil (список не закончился), то счетчик числа элементов увеличивается на 1. Далее происходит очередной вызов рекурсивной процедуры уже с адресом следующего элемента списка, а «текущая» рекурсивная процедура приостанавливается до окончания вызванной процедуры. Вызванная процедура работает точно так же: считает, вызывает процедуру и переходит в состояние ожидания. Формируется как бы последовательность из процедур, каждая из которых ожидает завершения вызванной процедуры. Этот процесс продолжается до тех пор, пока очередное значение адреса не станет равным Nil (признак окончания списка). В последней вызванной рекурсивной процедуре уже не происходит очередного вызова, так как не соблюдается условие q<>nil, срабатывает «ограничитель рекурсии». В результате процедура завершается без выполнения каких-либо действий, а управление возвращается в «предпоследнюю», вызывающую процедуру. Точкой возврата будет оператор, стоящий за вызовом процедуры, в данном тексте - End, и «предпоследняя» процедура завершает свою работу, возвращая управление в вызвавшую её процедуру. Начинается процесс «сворачивания» цепочки ожидающих завершения процедур. Счетчик count, вызывавшийся по ссылке, сохраняет накопленное значение после завершения всей цепочки вызванных рекурсивных процедур.
Если из текста рассмотренной процедуры убрать использование счетчика, то получится некий базисный вариант рекурсивной процедуры, который можно применять при решении других задач обработки списка: распечатать содержимое списка; определить, есть ли в списке элемент с заданным порядковым номером или определенным значением информационного поля; уничтожить список с освобождением памяти и др.
7.11.Бинарные деревья.
Кроме линейных структур существуют и нелинейные, при помощи которых задаются иерархические связи данных. Для этого используются графы, а среди них сетевые и древовидные структуры. Рассмотрим один вид деревьев - бинарное дерево.
Бинарное (двоичное) дерево - это конечное множество элементов, которое либо пусто, либо содержит один элемент, называемый корнем дерева, а остальные элементы множества делятся на два непересекающихся подмножества, каждое из которых само является бинарным деревом. Эти подмножества называются правым и левым поддеревьями исходного дерева.
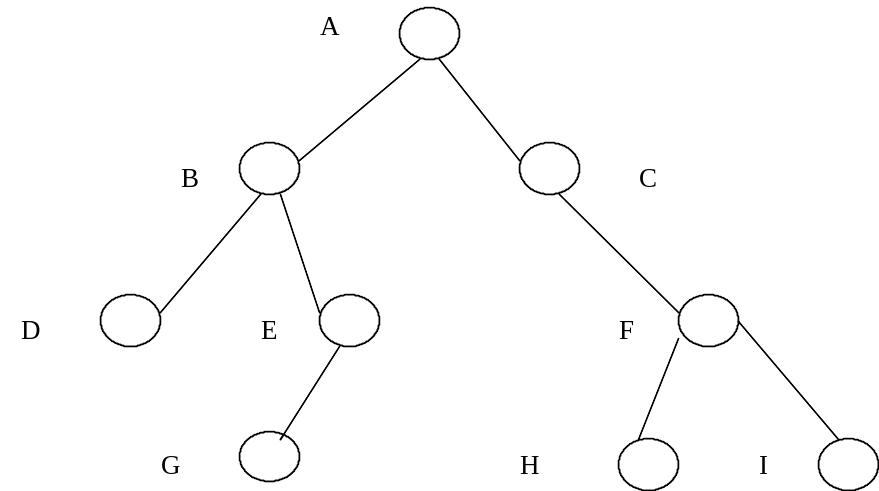
Рис. 8 Двоичное дерево
На рис. 8 показан наиболее часто встречающийся способ представления бинарного дерева. Оно состоит из девяти узлов. Корнем дерева является узел А. Левое поддерево имеет корень В, а правое поддерево - корень С. Они соединяются соответствующими ветвями, исходящими из А. Отсутствие ветви означает пустое поддерево. Например, у поддерева с корнем С нет левого поддерева, оно пусто. Пусто и правое поддерево с корнем Е. Бинарные поддеревья с корнями D, G, H и I имеют пустые левые и правые поддеревья. Узел, имеющий пустые правое и левое поддеревья, называется листом. Если каждый узел бинарного дерева, не являющийся листом, имеет непустые правое и левое поддеревья, то дерево называется строго бинарным
Уровень узла в бинарном дереве определяется следующим образом: уровень корня всегда равен нулю, а далее номера уровней при движении по дереву от корня увеличиваются на 1 по отношению к своему непосредственному предку. Глубина бинарного дерева - это максимальный уровень листа дерева, иначе говоря, длина самого длинного пути от корня к листу дерева. Узлы дерева могут быть пронумерованы по следующей схеме (см. рис. 9)
Рис. 9 Схема нумерации узлов двоичного дерева
Номер корня всегда равен 1, левый потомок получает номер 2, правый - номер 3. Левый потомок узла 2 должен получить номер 4, а правый - 5, левый потомок узла 3 получит номер 6, правый - 7 и т.д. Несуществующие узлы не нумеруются, что, однако, не нарушает указанного порядка, так как их номера не используются. При такой системе нумерации в дереве каждый узел получает уникальный номер.
Полное бинарное дерево уровня n - это дерево, в котором каждый узел уровня n является листом и каждый узел уровня меньше n имеет непустые правое и левое поддеревья.
Почти полное бинарное дерево определяется как бинарное дерево, для которого существует неотрицательное целое k такое, что:
каждый лист в дереве имеет уровень k или k+1;
если узел дерева имеет правого потомка уровня k+1, тогда все его левые потомки, являющиеся листами, также имеют уровень k+1.