Вопрос 55: Дуополия Стэкльберга.

В случае лидерства по объему выпуска одна из фирм делает свой выбор раньше другой. Иногда такую модель взаимодействия называют моделью Стэкельберга в честь первого экономиста, который подверг систематическому исследованию взаимодействия по типу "лидер-ведомый".

Модель Стэкельберга часто используется для характеристики отраслей, в которых существует одна доминирующая фирма, или естественный лидер. Обратимся к деталям данной теоретической модели. Предположим, что фирма 1 — лидер и что она решает производить объем выпуска y1192. Фирма 2 в ответ на это выбирает объем выпуска y2193. Каждая из двух фирм знает, что равновесная цена на рынке зависит от общего произведенного объема выпуска. Воспользуемся обратной функцией спроса p(Y), чтобы выразить равновесную цену как функцию отраслевого выпуска Y = y1 + y2194.

Какой объем выпуска следует выбрать лидеру, чтобы максимизировать свою прибыль? Ответ зависит от того, какова, по мнению лидера, будет реакция ведомого на сделанный им выбор. Лидер, по-видимому, должен ожидать, что ведомый также попытается максимизировать прибыль при данном выборе, сделанном лидером. Чтобы лидер мог принять разумное решение в отношении собственного производства, он должен рассмотреть задачу максимизации прибыли ведомого.

Мы предполагаем, что ведомый хочет максимизировать свою прибыль:

max p(y₁ + y₂) y₂ — c₂(y₂)195.

196Прибыль ведомого зависит от выбора объема выпуска лидером, но, с точки зрения ведомого, выпуск лидера предопределен — лидер уже осуществил производство, и ведомый просто считает его объем выпуска постоянным.

Ведомый стремится выбрать такой объем выпуска, при котором предельный доход равен предельным издержкам:

197.

Предельный доход имеет обычную интерпретацию. Когда ведомый увеличивает выпуск, он увеличивает свой общий доход, продавая больший объем выпуска по рыночной цене. Но он также снижает цену на Dp198, а это понижает прибыль, получаемую им на все те единицы выпуска, которые раньше продавались по более высокой цене.

Необходимо отметить следующий важный момент: выбор объема выпуска, максимизирующий прибыль ведомого, будет зависеть от выбора, сделанного лидером. Мы записываем эту взаимосвязь как

y₂ = f₂(y₁)199.

Функция f₂(y₁)200 представляет максимизирующий прибыль выпуск ведомого как функцию объема выпуска лидера. Эта функция называется функцией реакции, так как показывает, как будет реагировать ведомый на выбор объема выпуска лидером.

Выведем кривую реакции для простого случая линейной кривой спроса. Здесь функция спроса (обратная) принимает вид p(y₁ + y₂) = a — b(y₁ + y₂)201.202 Для удобства примем издержки равными нулю.

Тогда функцию прибыли для фирмы 2 можно записать в виде:

₂(y₁, y₂) = [a — b(y₁ + y₂)] y₂

₂(y₁, y₂) = ay₂ — by₁y₂ — .

Можно воспользоваться этим выражением, чтобы провести на рис.26.1 изопрофитные линии. Это линии, описывающие те комбинации y1203 и y2204, которые приносят фирме 2 постоянный уровень прибыли. Иными словами, изопрофитные линии состоят из всех точек (y1, y2205), удовлетворяющих уравнениям вида

ay₂ — by₁y₂ — = .

Обратите внимание, что по мере движения к изопрофитным линиям, расположенным левее, прибыль фирмы 2 будет возрастать. Это справедливо, потому что если фиксировать выпуск фирмы 2 на некотором уровне, то прибыль фирмы 2 будет увеличиваться по мере уменьшения выпуска фирмы 1. Максимально возможную прибыль фирма 2 получит в ситуации, когда она будет монополистом; иначе говоря, когда фирма 1 предпочтет производить ноль единиц выпуска.

При каждом возможном выборе объема выпуска фирмой 1 фирма 2 стремится выбрать свой собственный объем выпуска таким образом, чтобы как можно больше увеличить свою прибыль. Это означает, что для каждого выбранного y1 фирма 2 выберет такое значение y₂206, при котором она окажется на изопрофитной кривой, расположенной левее других (рис.26.1). Эта точка будет удовлетворять обычному условию касания: изопрофитная кривая в точке оптимального выбора должна быть вертикальна. Геометрическое место точек таких касаний описывает кривую реакции фирмы 2 — f₂(y₁)207.

Чтобы посмотреть, как выглядит данный результат алгебраически, необходимо иметь выражение для предельного дохода, связанного с функцией прибыли для фирмы 2. Это выражение задается следующим образом:

MR₂(y₁, y₂) = a — by₁ — 2by₂.

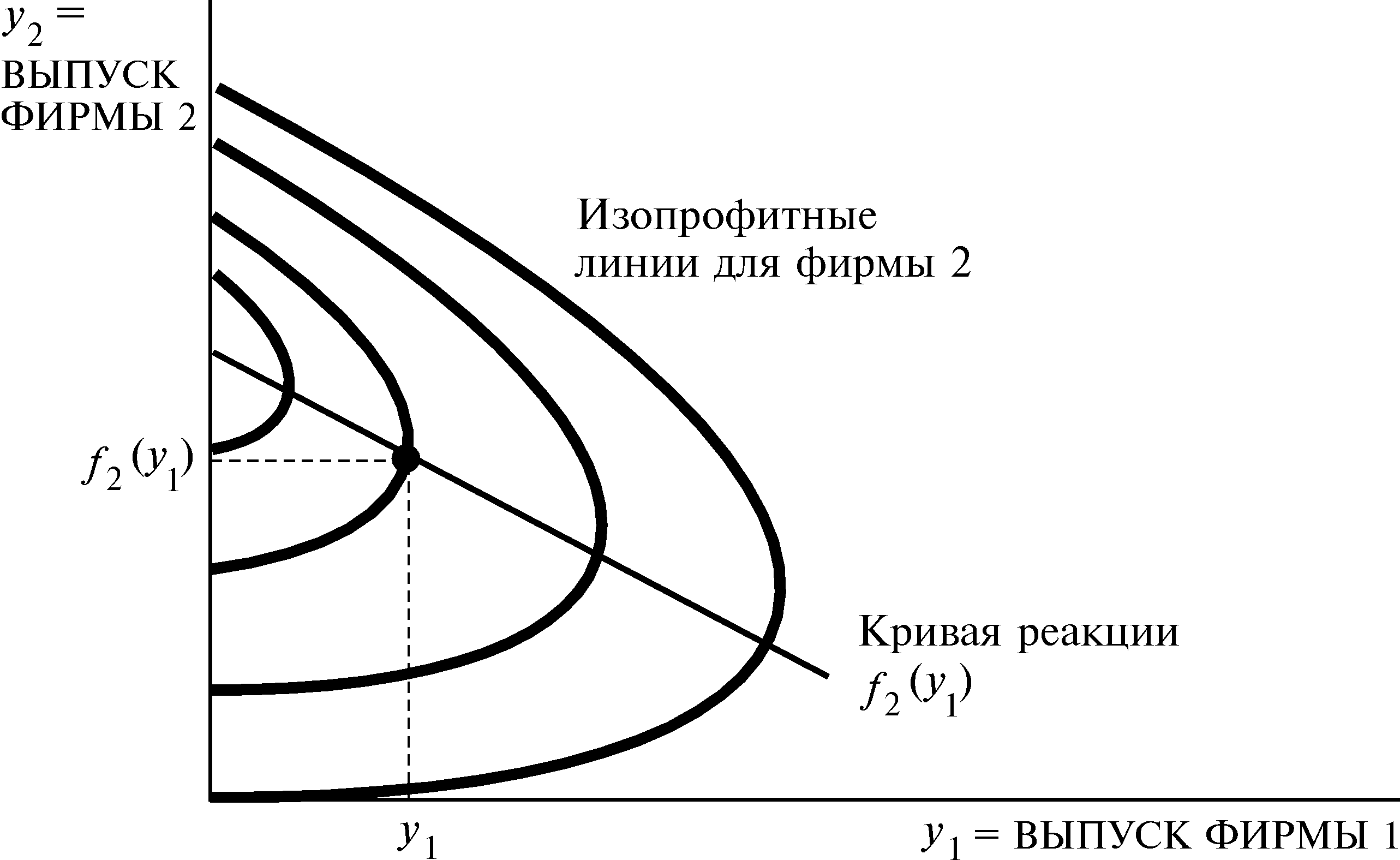
Рисунок 26.1 Выведение кривой реакции.

Приравняв предельный доход к предельным издержкам, которые в данном случае равны нулю, получаем уравнение

a — by₁ — 2by₂ = 0,

которое можно решить, выведя при этом кривую реакции фирмы 2:

208.

Эта кривая реакции есть прямая линия, изображенная на рис.26.1.

Обратимся теперь к задаче максимизации прибыли лидера.

Предположительно, лидер также осознает, что его действия оказывают влияние на выбор объема выпуска ведомым. Эта взаимосвязь в краткой форме выражена функцией реакции f₂(y₁)209. Следовательно, выбирая свой объем выпуска, лидер должен признавать влияние, оказываемое им на ведомого.

Задача максимизации прибыли лидером поэтому принимает вид

max p(y₁ + y₂)y₁ — c₁(y₁) 210

211при y₂ = f₂(y₁)212.

Подстановка второго уравнения в первое дает

max p[y₁ + f₂(y₁)]y₁ — c₁(y₁)213.

Обратите внимание на то, что лидер осознает, что при выборе объема выпуска y₁214 общий производимый выпуск составит y1 + f2(y1)215: его собственный выпуск плюс выпуск, производимый ведомым. Намереваясь изменить объем своего выпуска, лидер должен осознавать влияние, оказываемое им на ведомого. Рассмотрим это применительно к описанной выше линейной кривой спроса. Как мы видели выше, кривая реакции в этом случае задается уравнением

. (26.1)

Поскольку мы предположили, что предельные издержки равны нулю, прибыль лидера есть

₁(y₁, y₂) = p(y₁ + y₂)y₁ = ay₁ — — by₁y₂. (26.2)

Но выпуск ведомого y2HHHHHHHHH будет зависеть от выбора лидера в соответствии с функцией реакции y2 = f2(y1)IIIIIIIII.

Подставив выражение для y2JJJJJJJJJ из уравнения (26.1) в уравнение (26.2), получаем

₁(y₁, y₂) = ay₁ — — by₁ f₂(y₁) = ay₁ — — by₁ .

Упростив это выражение, имеем

₁(y₁, y₂) = y₁ — .

Предельный доход для этой функции есть

— by₁KKKKKKKKK.

Приравняв его к предельным издержкам, которые в этом примере равны нулю, и найдя из полученного уравнения y1LLLLLLLLL, получим

MMMMMMMMM.

Чтобы найти выпуск ведомого, просто подставляем NNNNNNNNN OOOOOOOOO в функцию реакции:

.PPPPPPPPP

Эти два уравнения дают общий отраслевой выпуск + 225 = 3a/4bRRRRRRRRR.

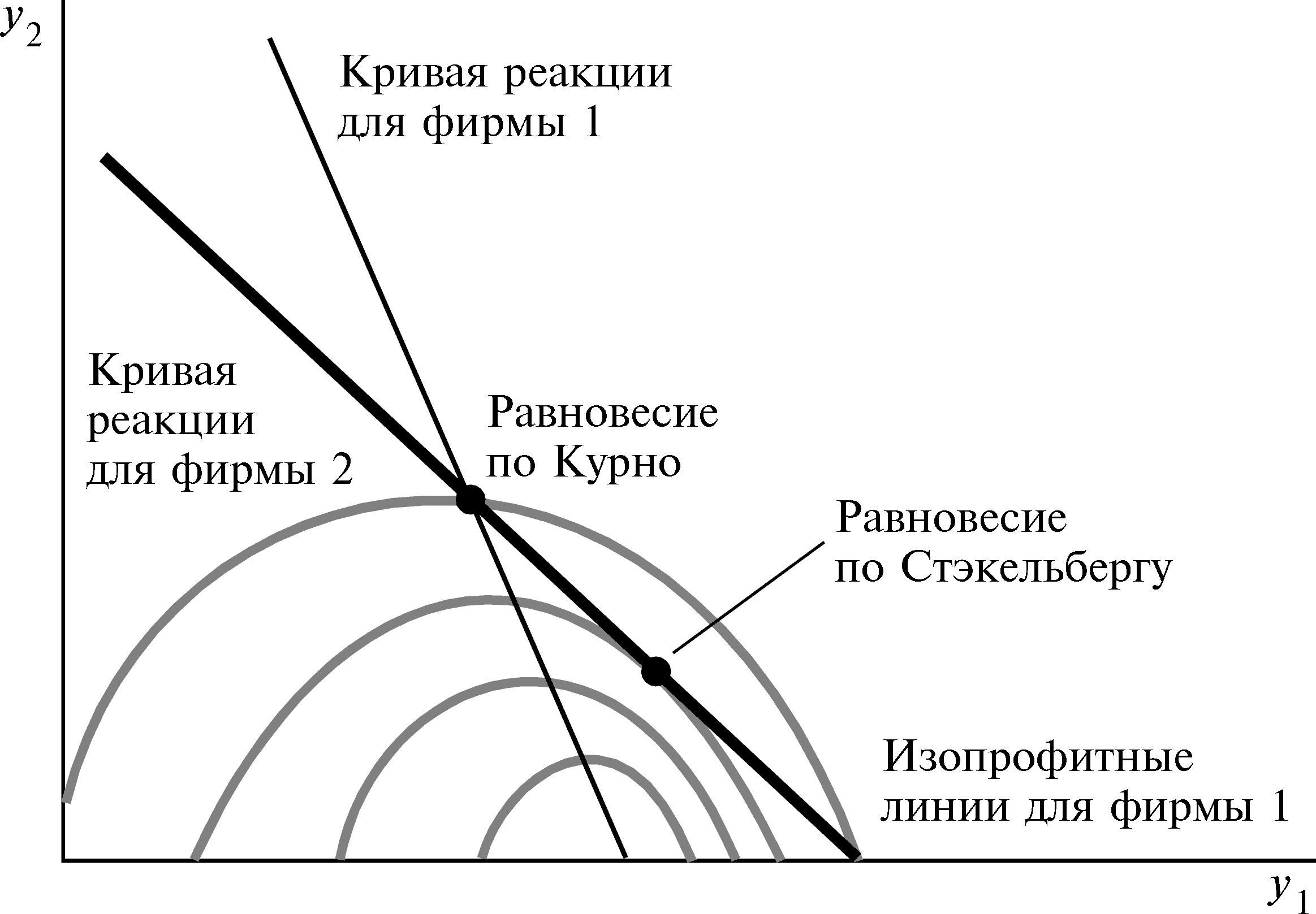
Решение по Стэкльбергу можно также проиллюстрировать графически с помощью изопрофитных кривых, представленных на рис.26.2. (Этот рисунок иллюстрирует также равновесие по Курно). Здесь мы изобразили кривые реакции для обеих фирм и изопрофитные кривые для фирмы 1. Изопрофитные кривые для фирмы 1 имеют ту же общую форму, что и изопрофитные кривые для фирмы 2; они просто повернуты на 90°. Более высокая прибыль для фирмы 1 связывается с более низкими изопрофитными кривыми, так как прибыль фирмы 1 будет расти по мере уменьшения выпуска фирмы 2.

Равновесие по Стэкльбергу. Фирма 1, лидер, выбирает ту точку на кривой реакции фирмы 2, в которой эта кривая касается самой низкой изопрофитной линии фирмы 1 из возможных, тем самым обеспечивая фирме 1 самую высокую прибыль из возможных.

Рис. 26.2

Фирма 2 ведет себя как ведомый, а это означает, что она будет выбирать выпуск, перемещаясь вдоль своей кривой реакции, f2(y1)SSSSSSSSS. Следовательно, фирма 1 хочет выбрать такую комбинацию выпуска на кривой реакции, которая дает ей наивысшую возможную прибыль. Но получение наивысшей возможной прибыли означает выбор такой точки на кривой реакции, в которой эта кривая касается самой низкой изопрофитной линии, как показано на рис.26.2. Что кривая реакции должна быть касательной к изопрофитной линии в данной точке — следует из обычной логики максимизации.