Вопрос 3: Кривые безразличия. Предельная норма замещения.

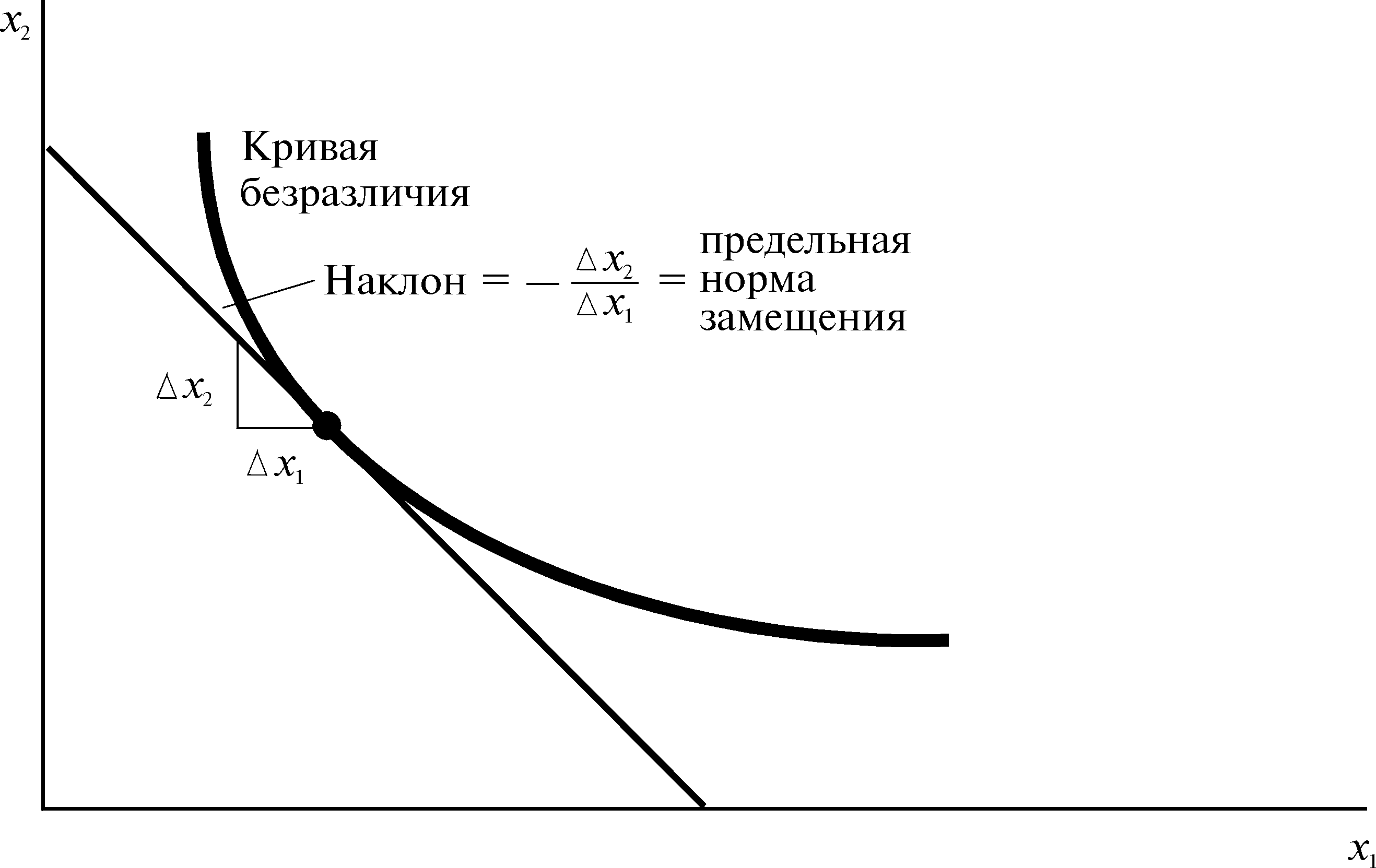
Всю теорию потребительского выбора можно описать графически, используя для этого построение, именуемое кривыми безразличия. Мы можем провести кривую безразличия через любой потребительский набор. Кривая безразличия, проходящая через какой-либо потребительский набор, состоит из всех товарных наборов, которые для потребителя не хуже заданного. Важный принцип, характеризующий кривые безразличия: кривые безразличия, представляющие отличные друг от друга уровни предпочтений, не могут пересекаться. Так же о кривых безразличия смотрите в ответе на первый вопрос (здесь и далее прим. авторов).

Наклон кривой безразличия известен как предельная норма замещения (MRS). Данное название проистекает из того факта, что MRS измеряет пропорцию, в которой потребитель готов заместить один товар другим. Предпосылка о монотонности предпочтений подразумевает отрицательный наклон кривых безразличия, поэтому в случае монотонных предпочтений поведение MRS всегда предполагает сокращение потребления одного товара ради получения большего количества другого. Случай выпуклых кривых безразличия указывает еще на один аспект поведения MRS. Для строго выпуклых кривых безразличия MRS — наклон кривой безразличия — по мере увеличения x₁ убывает (по абсолютной величине). Таким образом, кривые безразличия демонстрируют убывание предельной нормы замещения.

Вопрос 4: Оптимум потребителя в ординалистской концепции потребительского выбора.

На одном и том же графике изображены бюджетное множество и несколько кривых безразличия. Мы хотим найти тот набор из данного бюджетного множества, который находится на самой высокой кривой безразличия. Поскольку предпочтения стандартны, так что бóльшее предпочитается меньшему, можно ограничиться рассмотрением наборов, лежащих на бюджетной линии, не заботясь о тех наборах, которые находятся под ней.

Будем двигаться влево из исходного положения в правом углу бюджетной линии. По мере движения вдоль бюджетной линии мы замечаем, что переходим на все более и более высокие кривые безразличия. Мы остановимся, когда попадем на самую высокую кривую безразличия, которая лишь касается бюджетной линии. На рассматриваемом графике товарный набор, связываемый с самой высокой кривой безразличия, лишь касающейся бюджетной линии, обозначен (х₁^*,х₂^*). Выбор (х₁^*,х₂^*) является оптимальным выбором для потребителя. Множество наборов, которые он предпочитает (х₁^*,х₂^*), а именно, множество наборов, располагающееся над его кривой безразличия, не пересекает наборы, которые он может себе позволить приобрести, а именно, наборы под бюджетной линией. Таким образом, набор (х₁^*,х₂^*) — это наилучший набор, который потребителю по карману.

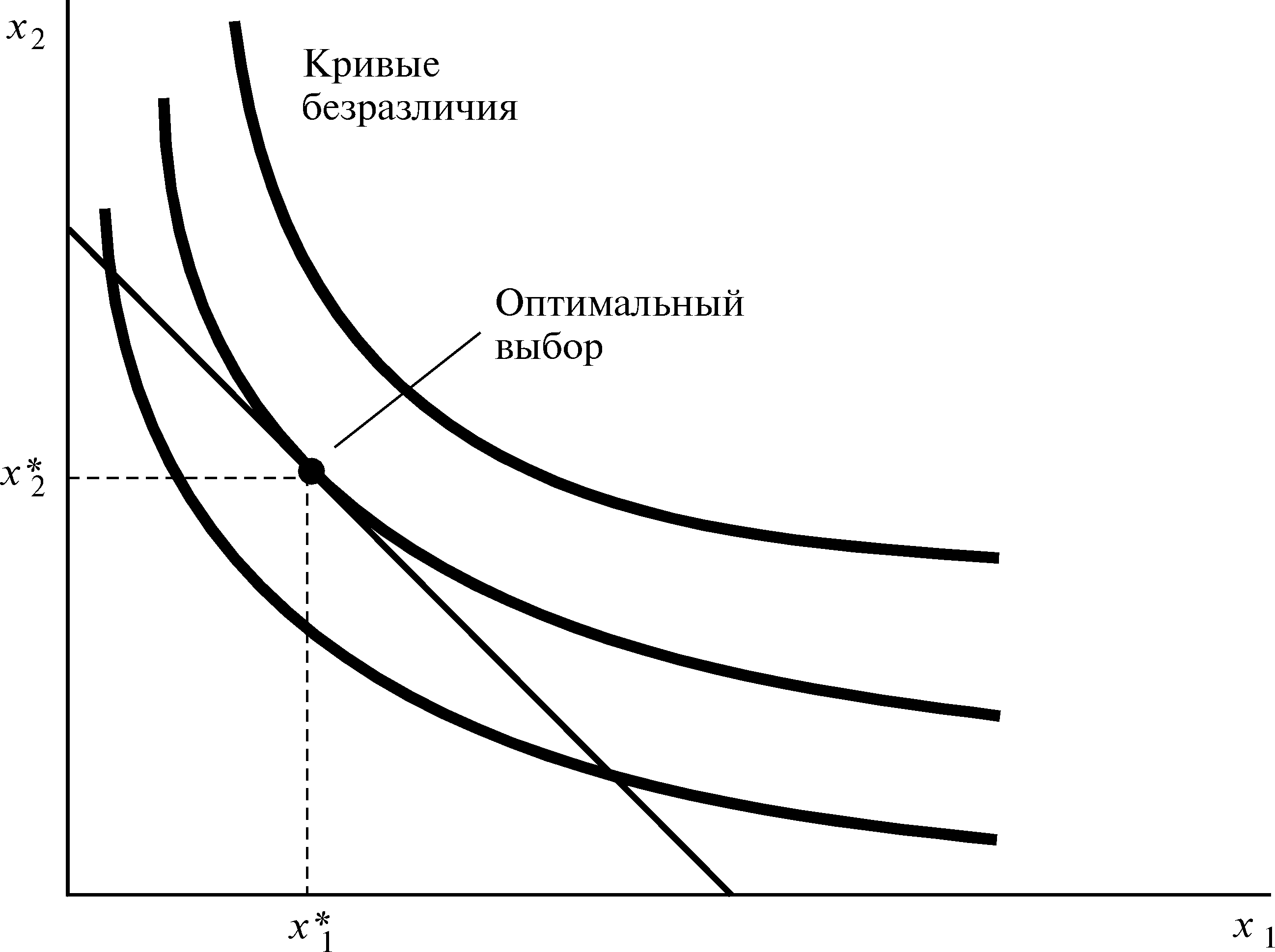
Рисунок 4.1 Оптимум потребителя

Так же следует уделить внимание случаям так называемых краевых оптимумов. Предположим, что в точке оптимума потребление какого-либо товара равно нулю, как на рис.4.2. Тогда наклоны кривой безразличия и бюджетной линии различны, однако кривая безразличия по-прежнему не пересекает бюджетной линии. Мы говорим, что на рис.4.2 представлен краевой оптимум, в то время как на рис.4.1 — внутренний оптимум. Если же мы хотим ограничиться рассмотрением лишь внутренних оптимумов, можно не рассматривать и пример краевых оптимумов. В случае внутреннего оптимума с плавно убывающими кривыми безразличия наклон кривой безразличия и наклон бюджетной линии должны быть одинаковы, потому что если бы они различались, кривая безразличия пересекла бы бюджетную линию, и мы не могли бы находиться в оптимальной точке.

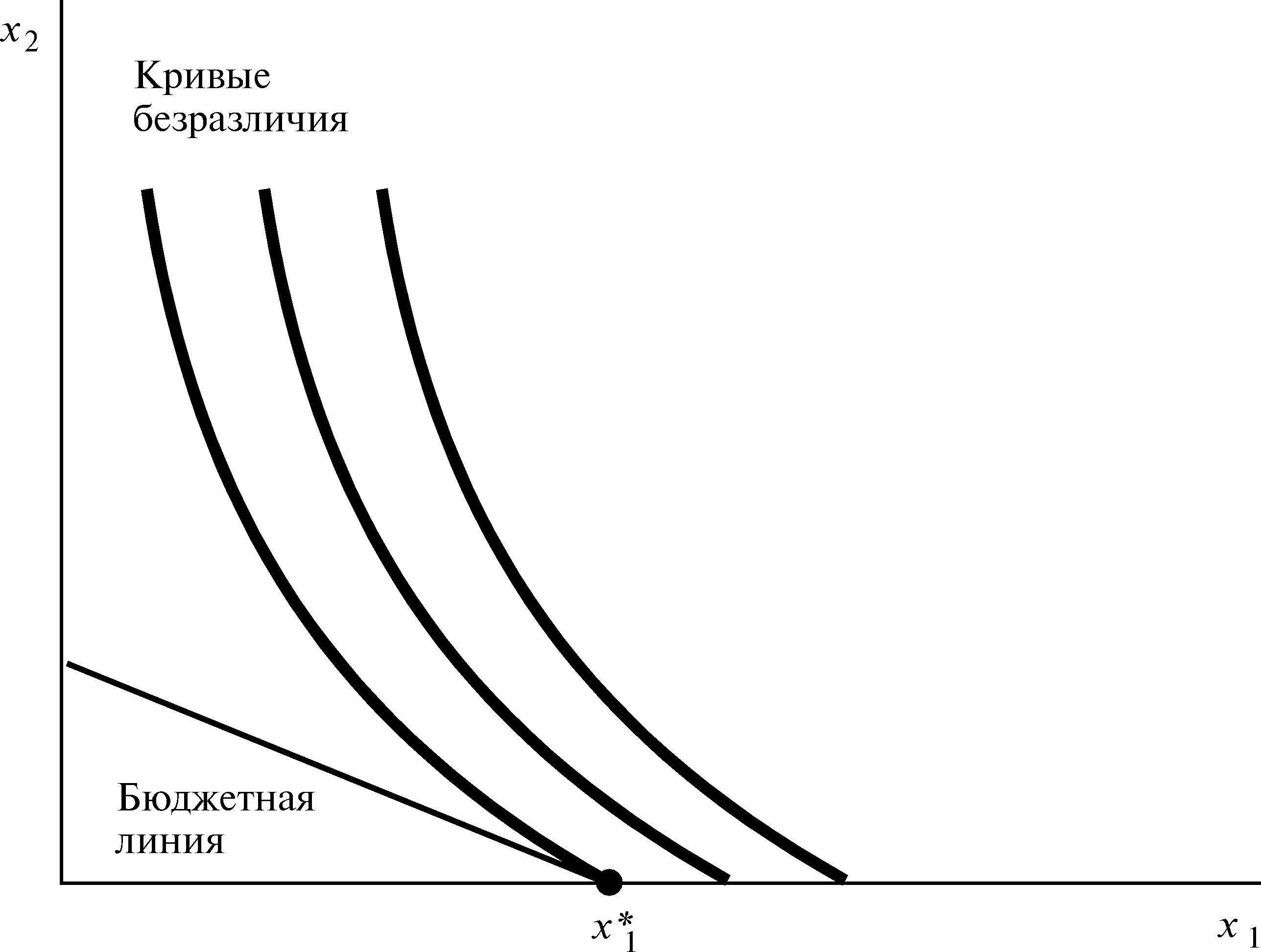
Рисунок 4.2 Краевой оптимум

Мы нашли необходимое условие, которому должен удовлетворять оптимальный потребительский выбор. Если оптимальный выбор предполагает потребление некоторого количества обоих товаров, т. е. речь идет о внутреннем оптимуме, то бюджетная линия с необходимостью будет выступать касательной к кривой безразличия.