Тело находится в равновесии, если равны нулю геометрическая сумма векторов всех приложенных к нему сил и алгебраическая сумма моментов этих сил относительно оси вращения.

При выполнении общего условия равновесия тело необязательно находится в покое. Согласно второму закону Ньютона при равенстве нулю равнодействующей всех сил ускорение тела равно нулю и оно может находиться в покое или двигаться равномерно и прямолинейно.

Равенство нулю алгебраической суммы моментов сил не означает также, что при этом тело обязательно находится в покое. На протяжении нескольких миллиардов лет с постоянным периодом продолжается вращение Земли вокруг оси именно потому, что алгебраическая сумма моментов сил, действующих на Землю со стороны других тел, очень мала. По той же причине продолжает вращение с постоянной частотой раскрученное велосипедное колесо, и только внешние силы останавливают это вращение.

Виды равновесия. В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемаяустойчивостью. Различают три вида равновесия тел: устойчивое, неустойчивое и безразличное. Равновесие называется устойчивым, если после небольших внешних воздействий тело возвращается в исходное состояние равновесия. Это происходит, если при небольшом смещении тела в любом направлении от первоначального положения равнодействующая сил, действующих на тело, становится отличной от нуля и направлена к положению равновесия. В устойчивом равновесии находится, например, шар на дне углубления

Равновесие называется неустойчивым, если при небольшом смещении тела из положения равновесия равнодействующая приложенных к нему сил отлична от нуля и направлена от положения равновесия

Диагамма растяжения

Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.

Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов).

Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.

Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.

В конечной точке происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована "шейка"

Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:

W=0,8F_max⋅Δl_max

По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.

Закон гука

Модель представляет собой демонстрацию, иллюстрирующую закон Гука. Вводится понятия «сила упругости» и «упругая деформация», формулируется закон Гука.

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

Простейшим видом деформации являются деформации растяжения и сжатия. При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:

Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м).

Виды деформаций при растяжении

Деформация растяжения возникает тогда, когда на стержень или трос действуют внешние силы, приложенные к их концам, направленные в разные стороны и совпадающие с продольной осью этих тел.При этом наблюдается не только удлинение тела, но и уменьшение площади его поперечного сечения

Кручение. Расчетные схемы, напряжения

Круче́ние — один из видов деформации тела. Возникает в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор — крутящий момент. На кручение работаютпружины растяжения-сжатия и валы.

При деформации кручения смещение каждой точки тела перпендикулярно к её расстоянию от оси приложенных сил и пропорционально этому расстоянию.

Угол закручивания цилиндрического стержня в границах упругих деформаций под действием момента T может быть определён из уравнения закона Гука для случая кручения

где:

 — геометрический полярный момент инерции;

 — длина стержня;

G — модуль сдвига.

Отношение угла закручивания φ к длине   называют относительным углом закручивания

Деформация кручения является частным случаем деформации сдвига.

Напряжения при кручении

Вращающийся стержень, работающий на кручение называют валом. Стержень, используемый как упругий элемент, который работает на скручивание, называется торсионом. Касательные напряжения  , возникающие в условиях кручения, определяются по формуле:

,

где r — расстояние от оси кручения.

Очевидно, что касательные напряжения достигают наибольшего значения на поверхности вала при   и при максимальном крутящем моменте  , то есть

,

где W_p — полярный момент сопротивления.

Это даёт возможность записать условие прочности при кручении в таком виде:

.

Используя это условие, можно или по известным силовым факторам, которые создают крутящий момент Т, найти полярный момент сопротивления и далее, в зависимости от той или иной формы, найти размеры сечения, или наоборот — зная размеры сечения, можно вычислить наибольшую величину крутящего момента, которую можно допустить в сечении, которое в свою очередь, позволит найти допустимые величины внешних нагрузок.

Деформация при кручении.

Деформация кручения выражается в скручивании тела под действием моментов внешних сил.

Представим цилиндрический стержень, один конец которого закреплен неподвижно, а другой нагружен крутящим моментом М_к пары сил Р. Если мысленно рассечь стержень поперечно в любом месте, то, для сохранения равновесия отсеченной части, к ней надо приложить некоторый момент М_x, равный по величине, но противоположный по направлению моменту М_к. Уравновешивающий момент М_к создается в поперечном сечении касательными напряжениями τ, возникающими вследствие действия внутренних сил сцепления частиц, из которых состоит материал стержня.

Понятно, что под действием момента внешних сил все сечения цилиндра, кроме закрепленного, поворачиваются. Угол φ поворота свободного торца стержня называется абсолютным углом закручивания.

Относительное круговое смещение сечений стержня друг относительно друга характеризуется углом γ, который называют относительным сдвигом.

Относительный сдвиг приобретает наибольшее значение на периферии цилиндра и приближается к нулю у его оси.

По аналогии можно записать прямо пропорциональную зависимость между касательными напряжениями и относительным сдвигом при кручении

τ = G • γ,

где G — модуль упругости при сдвиге, кгс/см² (Па).

Можно сделать вывод, что с учетом характера изменения относительного сдвига касательные напряжения при кручении изменяются от нуля в центре сечения до максимума на его периферии.

Наибольшие действительные касательные напряжения при кручении обычно вычисляют по формуле

τ_к = М_к / W_р

где М_к — крутящий момент внешних сил, кгс•см (Н•м);

W_р— полярный момент сопротивления сечения, см³.

Для круглых сплошных сечений полярный момент определяется из равенства

W_p ≈ 0,2d³,

где d — диаметр сечения, см.

Валы, подверженные деформации кручения, проверяются на прочность и жесткость.

Прочность вала определяется из условия

τ_к =М_к / W_p ≤ [τ]_к,

где [τ]_к — допустимое напряжение при кручении.

Жесткость устанавливают по допустимой величине абсолютного угла закручивания φ, действительные значения которого в радианах определяют по формуле

φ = М_кl / GI_p,

где l —длина стержня, см;

I_p — полярный момент инерции сечения, см⁴;

G — модуль упругости при сдвиге.

Для круглого сплошного сечения полярный момент инерции равен

I_p ≈ 0.1d⁴.

Изгиб. Расчетные схемы, напряжения

Изгиб — вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев. Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Прямой изгиб возникает в случае, когда изгибающий моментв данном поперечном сечении бруса действует в плоскости, проходящей через одну из главных центральных осей инерции этого сечения. В случае, когда плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных осей инерции этого сечения, называется косым.

Если при прямом или косом изгибе в поперечном сечении бруса действует только изгибающий момент, то соответственно имеется чистый прямой или чистый косой изгиб. Если в поперечном сечении действует также и поперечная сила, то имеется поперечный прямой илипоперечный косой изгиб.

Часто термин «прямой» в названии прямого чистого и прямого поперечного изгиба не употребляют и их называют соответственно чистым изгибом и поперечным изгибом.

Mx, Q - внутренние усилия: изгибающий момент и поперечная сила, они изменяются вдоль бруса и определяются с помощью построения эпюр;

у - координата точек поперечного сечения, в которых определяются напряжения;

b - ширина сечения в месте определения касательных напряжений;

Jx - главный центральный момент инерции -момент инерции относительно центральной оси х,

сx* - статический момент относительно нейтральной оси ж той части площади поперечного сечения, которая расположена выше (или ниже) продольного сечения - выше или ниже уровня у, в точках которого определяются касательные напряжения.

Эти формулы выведены в главных центральных осях поперечного сечения бруса. На рис. 5.1 это оси X, У. При этом ось Y совпадает с осью симметрии сечения, а ось X, перпендикулярная плоскости изгиба, проходит через центр тяжести сечения и является нейтральной осью: нормальные напряжения в точках этой оси равны нулю. Ось Z - ось бруса.

Таким образом, на уровне у напряжения, определяемые вышеприведенными формулами, постоянны, не зависят от координаты X.

С увеличением координаты у нормальные напряжения увеличиваются и в наиболее удаленных от нейтральной оси точках достигают наибольшего значения:

Для расчетов используется специальная геометрическая характеристика - момент сопротивления сечения при изгибе:

Касательные напряжения, наоборот, уменьшаются и в наиболее удаленных от нейтральной оси точках обращаются в нуль, а а области нейтральной оси достигают наибольших значений (рис. 5.1,г). Кроме того, наибольшие значения касательных напряжений значительно меньше максимальных значений нормальных напряжений: так для консольного стержня прямоугольного поперечного сечения, нагруженного сосредоточенной силой на свободном конце, отношение максимальных значений этих напряжений

где l, h - длина бруса и высота его поперечного сечения.

Поэтому, при l >> h, что имеет место в большинстве случаев, касательные напряжения по сравнению с нормальными пренебрежимо малы и при расчетах на прочность не учитываются.

Условие прочности имеет следующий вид:

- допускаемое напряжение.

Процесс расчета бруса на прочность следует вести в определенной последовательности. При этом необходимо:

Определить весь комплекс внешних сил, в том числе и реакций опор.  Прежде всего, необходимо определить все реакции опор, так как реакции входят в число внешних сил. Если при этом число реакций равно числу линейно независимых уравнений статики, то все реакции находятся из статических уравнений. Построить эпюры внутренних усилий, по которым определить опасные сечения.  Построение эпюр внутренних усилий выполняется с использованием метода сечений и начинается с деления бруса на участки. Границами участков служат места приложения сосредоточенных сил или моментов, места начала и конца действия распределенных нагрузок.

Далее на каждом участке выбирается произвольное сечение, для которого составляются выражения для определения внутренних усилий, по которым строятся эпюры (графики) этих усилий.

По эпюрам внутренних усилий определяются опасные сечения, в которых эти усилия достигают наибольших значений.

В большинстве случаев основным внутренним усилием при расчетах бруса на прочность является изгибающий момент и связанные с ним нормальные напряжения.

3. В опасных сечениях определить максимальные нормальные напряжения и для наибольшего из этих напряжений проверить выполнение условия прочности.

После определения положения опасных сечений с наибольшими значениями изгибающих моментов, в этих сечениях вычисляют наибольшие нормальные напряжения:

а) Для брусьев из пластичного материала, при равенстве по величине пределов текучести при растяжении и сжатии, наибольшие расчетные напряжения возникают в "опасных" точках, которые наиболее удалены от нейтральной оси.

Эти напряжения сравниваются с допускаемым напряжением  :

после чего делается заключение о прочности бруса.

б) Если же брус изготовлен из хрупкого материала: , то в опасных сечениях наибольшие нормальные напряжения определяются и в растянутых, и в сжатых   зонах поперечного сечения и путем сравнения их с соответствующими допускаемыми напряжениями при растяжении   и сжатии  :

Определение реакции опор

Реакциями опор называют усилия, возникающие в опорах и удерживающие элемент находящийся под действием внешних нагрузок в состоянии статического равновесия.

Проще говоря, опорные реакции это ровно те силы и моменты, которые необходимы для того, чтобы брус на который действует система заданных внешних нагрузок не вращался и не перемещался в пространстве.

При решении задач сопротивления материалов часто возникает необходимость определить реакции для конструкции или ее элементов. 

Дело в том, что реакции также выступают в роли внешних нагрузок приложенных к рассматриваемому элементу.

Как правило, для упрощения расчетов, реактивные силу и момент раскладывают на составляющие

- полный вектор силы R проецируется на все три оси системы координат (x, y и z);

- момент M разбивается на три составляющие момента относительно тех же осей.

В итоге для общего (пространственного или объемного) случая нагружения имеем 6 составляющих реакций - три силы - R_x, R_y, R_z (рис. 1а) и три момента M_x, M_y, M_z (рис. 1б).

В случае, когда все внешние нагрузки лежат в одной плоскости, количество реакций в общем случае сокращается до трех: двух сил (вертикальной R_y и горизонтальной R_z) и момента M_x.

При растяжении-сжатии, для удержания бруса в статичном состоянии достаточно одной силы, приложенной вдоль его оси.

Все реакции легко определяются из уравнений статики (неподвижности системы).

Для общего случая нагружения, где может возникать 6 реакций опор, потребуется минимум 6 уравнений (по одному уравнению на каждую неизвестную реакцию).

Из условия, что заданная система не перемещается в пространстве (вправо-влево, вверх-вниз, а также, вперед-назад) можем приравнять к нулю сумму проекций всех сил на оси  x, y и z.

∑F(x)=0;   ∑F(y)=0;   ∑F(z)=0.

Из условия, что система не вращается, приравниваем к нулю сумму моментов, создаваемых всеми нагрузками относительно соответствующих осей.

∑m(x)=0;   ∑m(y)=0;   ∑m(z)=0.

Совместное решение системы полученных уравнений покажет величину и направление реакций в опорах.

Величина некоторых реакций в некоторых случаях может быть равна нулю, это говорит о том, что активные нагрузки и остальные реакции взаимно уравновешиваются таким образом, что для удержания системы в состоянии покоя, в данной точке опоры не требуется.

Системы, в которых реакции опор нельзя определить с помощью одних только уравнений статики называют статически неопределимыми.

Внутренние силовые факторы при изгибе

Под влиянием внешей нагрузки реальные тела деформируются, в отличие от абсолютно твердого тела, изучаемого в курсе теоретической механики. При этом между рядом раположенными частицами тела воникают, по законам физики, внутренние силы. Если мысленно рассечь деформированный брус плоским перечным сечением на две части и привести внутренние силы, действующие со стороны одной части на другую - к центру тяжести (площади) поперечного сечения, получим ГЛАВНЫЙ ВЕКТОР R и ГЛАВНЫЙ МОМЕНТ M системы этих внутренних сил. Эти величины (R и M) имеют такой смысл: Если мысленно заменить внутренние силы, действующие в сечении, силой R и моментом (парой сил) M (приложив их в центре тяжести поперечного сечения), то равновесие отсеченной части тела не нарушится. То есть R и M (совместно) являются статическим эквивалентом системы внутренних сил, действующих в сечении.

Знаки ВСФ

В сопротивлении материалов принято следующее ПРАВИЛО ЗНАКОВ для ВСФ.:

Продольная сила N считается положительной, если она направлена в сторону ВНЕШНЕЙ нормали к сечению, то есть РАСТЯГИВАЕТ элемент, показанный на рис 4.4 и отрицательной, если она СЖИМАЕТ элемент.

Поперечная сила Q_Y (при расчете балок и плоских рам она обычно обозначается просто Q) считается положительной, если она направлена в сторону внешней нормали к сечению, ПОВЕРНУТОЙ на 90^o ПО ЧАСОВОЙ СТРЕЛКЕ.

Изгибающий момент M_X считается положительным (для БАЛОК и горизонтальных участков РАМ), если он деформирует продольную ось бруса 

выпуклостью вниз (т е сжатые продольные "волокна" расположены сверху, а растянутые - снизу - см рис 5). В противном случае (выпуклостью вверх, сжатые волокна внизу, растянутые - вверху) изгибающий момент считается отрицательным. Здесь: ось X перпендикулярна плоскости рисунка 4.4 и проходит через точку С - центр тяжести (площади) поперечного сечения. При расчете балок и плоских рам M_X обычно обозначается просто M.

Все ВСФ, показанные на рис. 4.4 ПОЛОЖИТЕЛЬНЫ. И в дальнейшем - неизвестные ВСФ будем предполагать ПОЛОЖИТЕЛЬНЫМИ. Тогда полученные в результате решения значения (включая знак) легко понять.

Эпюры ВСФ

График зависимости величины какого-либо ВСФ от координаты z поперечного сечения, в котором действует этот ВСФ называется ЭПЮРОЙ. Эпюры имеют большое значение в расчетах на прочность, так как позволяют легко определить сечение, в котором брус максимально нагружен (если поперечное сечение одинаково по всей длине бруса). Такое сечение называется ОПАСНЫМ сечением.

Чистый изгиб. Расчетные схемы

Чистый изгиб – такой вид нагружения, при котором в поперечных сечениях бруса возникают только изгибающие моменты Мх, а Q=0.

Чистый изгиб характерен тем, что из шести компонентов внутренних усилий только изгибающий момент не равен 0, а поперечные и нормальные силы отсутствуют. Для тех участков стержня, где соблюдается это условие, изгибающий момент остается постоянным (М = const). Изгибающий момент численно равен сумме моментов всех внешних сил, действующих на отсеченную часть балки относительно оси Ох. Эпюра изгибающих моментов строится на сжатом волокне. При этом изгибающий момент в балках считается положительным, если сжаты верхние волокна, т. е. элемент изгибается выпуклостью вниз.

1. Статическая сторона задачи:

Условия чистого изгиба могут возникать при различных внешних нагрузках.

. Геометрическая сторона задачи:

При изгибе под действием моментов М ось балки искривляется (установлено экспериментально).

3. Физическая сторона задачи:

При чистом изгибе вводится предположение о ненадавливаемости продольных слоев 

Напряжения при чистом изгибе

Определение напряжений в поперечном сечении производится в предположении, что продольные волокна при деформации бруса не надавливают друг на друга, а поперечные сечения, плоские и  нормальные к продольной оси до деформации, остаются плоскими и нормальными к продольной оси и после деформации, т.е. поворачиваются на некоторый угол   относительно неподвижной точки, а материал бруса подчиняется закону Гука:  .

Выделим в зоне чистого изгиба элементарный участок длиной dz. При изгибе длина этого участка, расположенного  по нейтральному слою,

 

,

 где   –  радиус кривизны нейтрального слоя;   –  угол поворота поперечных сечений, расположенных на расстоянии dz.

Продольные волокна, расположенные на расстоянии у от нейтрального слоя, получат абсолютные удлинения

 

.

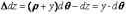 Относительное удлинение

 

.

 Соответственно, закон Гука при чистом изгибе имеет вид:

 

,                                          (2.47)

 т.е. характер изменения нормальных напряжений по поперечному сечению имеет линейный вид. Нейтральная ось делит поперечное сечение бруса на две части, в одной из которых возникают растягивающие, в другой – сжимающие напряжения.

Косой изгиб

Косым изгибом называется такой вид изгиба, при котором плоскость нагрузки (силовая линия) изгибающего момента не совпадает ни с одной из главных осей инерции поперечного сечения стержня X, Y (рис. 7.1, а, б).

При косом изгибе действующие внешние силы (моменты) представляют их проекциями на главные оси поперечного сечения (рис. 7.1, б), тем самым сводят задачу к случаю поперечного изгиба в двух главных плоскостях. Из рис. 7.1, а, б видно, что:

Изгибающие моменты в расчетном сечении:

Правило знаков. Изгибающие моменты в расчетном поперечном сечении считаются положительными, если они вызывают в первом (заштрихованном) октанте напряжения растяжения.

Нормальные напряжения в точках поперечного сечения с текущими координатами х, у определяются алгебраической суммой напряжений, вызываемых изгибающими моментами Мx и Мy:

где Jx и Jy — моменты инерции поперечного сечения относительно главных, центральных осей инерции сечения X, Y, т. е. изменяются по линейному закону. Уравнение нейтральной (нулевой) линии в сечении

Опасные сечения и точки при косом изгибе

Опасным является то сечение, в котором эквивалентный момент будет наибольшим.

Опасные точки – это 2 точки поперечного сечения, в которых одновременнонормальные напряжения от изгиба и касательные напряжения от кручения имеют наибольшие значения. Опасные точки расположены вблизи контура поперечного сечения вала. Поскольку валы, как правило, изготавливают из пластичного материала, обе опасные точки равноопасны.

Изгиб с кручением

Данный вид деформации имеет место когда в сечениях одновременно возникают изгибающий и скручивающий моменты

Условие прочности 

              Эквивалентный момент М_экв рассчитывается по одной из гипотез прочности:

Расчетные схемы при изгибе с кручением