Условия эксплуатации приборных комплексов ЛА

Авиационные приборы эксплуатируются в условиях воздействия климатических, механических и других факторов. Интенсивность воздействия таких факторов на приборы зависит от типа летательного аппарата, его летно-технических характеристик и места установки авиационных приборов на летательном аппарате. К климатическим факторам относятся прежде всего температура, давление и влажность воздуха. Температура окружающего воздуха может изменяться в пределах от +60 до —60° С, температура воздуха в не герметизируемых зонах летательного аппарата может достигать +100° С, а в зоне двигателя до +300° С. Изменение температуры влияет на линейные размеры деталей, упругость чувствительных элементов и пружин, электрическое сопротивление проводников и магнитное сопротивление магнитопроводов, состояние смазки трущихся деталей, состояние пластмасс изоляционных материалов. Для снижения вредного влияния температуры на авиационные приборы выбирают материалы с малыми температурными коэффициентами, применяют термостатирование и устройства температурной компенсации, используют специальные смазки и т. д.

Снижение давления ухудшает отвод тепла от приборов, усиливает испарение смазки, уменьшает напряжение пробоя изоляции, ухудшает коммутацию, снижает работоспособность негерметичных приборов. Для предотвращения вредных последствий влияния пониженного атмосферного давления применяют изоляционные материалы повышенного качества, уменьшают количество контактных групп, улучшают герметичность приборов, трубопроводов и отсеков с оборудованием.

Относительная влажность воздуха может изменяться от 0 до 100% при высотных полетах и при полетах в нижних слоях атмосферы. Для авиационных приборов наиболее опасна повышенная влажность воздуха, которая ухудшает электрическую изоляцию деталей, изменяет диэлектрическую проницаемость материалов, ускоряет коррозию металлов, создает угрозу заклинивания подвижных частей приборов или закупорки трубопроводов при возможном замерзании влаги. Для уменьшения влияния повышенной влажности на авиационные приборы производят осушку воздуха в кабинах и отсеках, применяют нержавеющие материалы, лакокрасочные и гальванические покрытия, используют пластмассы с пониженным водопоглощением, применяют герметизацию и обогрев приборов.

К механическим факторам относятся ускорения, удары, вибрации и шумы. Воздействие механических факторов вызывает смещение положения равновесия подвижных частей приборов при наличии небаланса, увеличение зоны застоя в опорах, нарушение прочности узлов крепления, обрывы проводов в местах пайки, ускоренный износ осей, опор и подшипников, снижение точности работы приборов. Для уменьшения влияния механических факторов на приборы используются индивидуальная амортизация приборных досок, тщательная балансировка подвижных частей приборов, прочные и твердые конструкционные материалы, специальная обработка деталей, обязательная проверка изготовленных приборов на воздействие механических факторов.

К другим эксплуатационным факторам относятся солнечная радиация, пыль, дождь, снег, электрические и магнитные поля и др. Против этих факторов в авиационных приборах также используются определенные защитные меры. Разработка авиационных приборов осуществляется с учетом перечисленных эксплуатационных факторов. Изготовленные приборы в соответствии с требованиями действующих стандартов подвергаются испытаниям на воздействие указанных эксплуатационных факторов.

Основные требования к механизмам авиационнх приборов

Понятие о структуре механизмов. Звено, кинематическая пара

Механи́зм— это совокупность совершающих требуемые движения тел (обычно — деталей машин), подвижно связанных и соприкасающихся между собой. Механизмы служат для передачи и преобразования движения.

Кинематической парой называется подвижное соединение двух звеньев. Кинематические пары классифицируются по различным признакам:

1) По числу связей, накладываемых на относительное движение звеньев, соединенных в кинематическую пару. По этому признаку кинематические пары подразделяются на классы. Приняты следующие обозначения:

W – число степеней свободы

S – число связей, накладываемых на относительное движение звеньев.

Свободное звено в пространстве имеет шесть степеней свободы. При соединении звеньев некоторые из этих степеней свободы отнимаются ("накладываются связи"). Зависимость между числом накладываемых связей и оставшимся числом степеней свободы в относительном движении звеньев очевидна:

W=6–S

или

S=6–W,

таким образом, существует пять классов кинематических пар (если отнять все шесть степеней свободы, то получится неподвижное соединение). 

Низшие кинематические пары обладают большей несущей способностью, т.к. имеют большую площадь контакта (в высшей паре площадь контакта теоретически равна нулю, а реально получается за счет деформации элементов кинематической пары – «пятно контакта"). Но в низших парах при работе происходит скольжение одной поверхности относительно другой, в то время как в высших парах может происходить и скольжение и качение. Звено – это деталь или группа деталей, представляющих с кинематической точки зрения единое целое (т.е. группа деталей, жестко соединенных между собой и движущихся как единое твердое тело). 

Кинематическая цепь – это сочетание звеньев, соединенных в кинематические пары. Имеется определенная классификация кинематических цепей – цепи могут быть простыми и сложными, замкнутыми (закрытыми) и разомкнутыми (открытыми), пространственными и плоскими. 

Ранее считалось, что механизм может быть сформирован только на основе замкнутой цепи. Однако с развитием робототехники в качестве механизмов стали широко применяться разомкнутые (открытые) цепи. Поэтому данная классификация в некоторой степени утратила свое первоначальное значение.

Степень подвижности плоского механизма

Формула а. П. Малышева для пространственных механизмов

Важнейшей характеристикой кинематической цепи является число степеней свободы.

Пусть кинематическая цепь содержит n звеньев. До того как они были соединены посредством кинематических пар, система из n звеньев имела 6n степеней свободы. Каждая кинематическая пара m класса дает m уравнений связей относительно координат. Разность между числом степеней свободы и числом уравнений связей дает число независимых координат - степеней подвижности механизма:

W= 6n - 1P₁ - 2P₂ - 3P₃ - 4P₄ - 5P₅.

где n - число подвижных звеньев;

6n- общее число степеней свободы всех звеньев;

P₁, P₂, P₃, Р₄ , P₅ — число кинематических пар от 1 до 5 класса;

W- степень подвижности механизма.

Формула п. Л. Чебышева для плоских механизмов

Для плоского механизма используется формула Чебышева:

W=3n-1P₄-2P₅

где n-число подвижных звеньев

P₄,P₅-кинематические пары с одной и с двумя наложенными связями.

По-другому эту формулу можно записать в следующем виде:

W=3n-2Pн-Pв

где n-общее число подвижных звеньев механизма

Рн - число низших кинематических пар

Рв — число высших кинематических пар

Передаточное отношение при поступательном и вращательном движениях

Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной самой себе.   При поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. При поступательном движении общую для всех точек тела скорость  V называют скоростью поступательного движения тела, а ускорение a – ускорением поступательного движения. Вращательным называется такое движение твердого тела, при котором любые две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными. Прямая, проходящая через две неподвижные точки, называется осью вращения. Уравнение γ = f(t) выражает закон вращательного движения твердого тела, где γ – угол поворота тела. Основными кинематическими характеристиками вращательного движения твердого тела являются егоугловая скорость ω и угловое ускорение ε. Угловая скорость тела в данный момент времени численно равна первой производной от угла поворота по времени: ω =  Угловое ускорение тела в данный момент времени численно равно первой производной от угловой скорости или второй производной от угла поворота тела по времени: ε =  Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает – замедленным. Если угловая скорость тела остается во все время движения постоянной (ω = const), то вращение тела называется равномерным. Если угловое ускорение тела во все время движения постоянно (ε = const), то вращение называетсяравнопеременным. Линейная скорость точки v вращающегося твердого тела численно равна произведению угловой скорости тела ω на расстояние R от этой точки до оси вращения.  v = ωR. Линейная скорость направлена по касательной к описываемой точкой окружности или перпендикулярно к плоскости, проходящей через ось вращения. Так как для всех точек тела угловая скорость ω имеет в данный момент одно и то же значение, то следует, что линейные скорости точек вращающего тела пропорциональны их расстояниям от оси вращения 

U=w1/w2

Понятие о высших и низших кинематических парах

Кинематической парой называется подвижное соединение двух соприкасающихся тел, например поршень и цилиндр, вал и подшипник и др. Тела, составляющие кинематическую пару, называются звеньями. Звено механизма может состоять из нескольких деталей (отдельно изготовляемых частей механизма), не имеющих между собой относительного движения.

По характеру соприкосновения элементов кинематические пары делятся на два основных класса: низшие и высшие. У низших кинематических пар соприкосновение звеньев происходит по поверхностям, а у высших — по линиям или точкам.

Силы действующие в механизмах

Звенья механизма придут в движение лишь тогда, когда на них будут действовать внешние силы, называемые движущими. Так, домкрат и лебедка поднимают груз в том случае, если к ним приложена мускульная сила человека или сила двигателя. Части механизма часов движутся благодаря силе упругости пружины или весу гири. Зубчатые колеса в коробке скоростей станка вращаются под действием силы электродвигателя.

При установившемся движении механизма требуется постоянное действие движущих сил. В то же время, если это действие прекращается, механизм останавливается. Это происходит потому, что в каждом механизме действуют силы, препятствующие движению.  Важнейшими силами сопротивления являются силы трения, возникающие во вращательных и поступательных кинематических парах.

Трение в, механизмах делится на два вида: трение скольжения и трение качения. При скольжении твердых тел трение вызывается тем, что неровности одного тела задевают за неровности другого. При этом происходит разрушение трущихся поверхностей, отчего и возникает сопротивление при скольжении. Известно, .что при скольжении несмазанных поверхностей величина силы трения прямо пропорциональна, силе давления, действующей перпендикулярно к поверхностям, т. е, в начале движения тел сила трения больше, чем при установившемся равномерном движении.

Опыты показали, что величина коэффициента трения зависит от материала трущихся поверхностей и чистоты их обработки. Уменьшение трения сопряженных тел достигается введением смазки между .трущимися поверхностями. Смазка влияет не только на величину силы трения, но и на характер ее зависимости от скорости движения. Сила трения направлена всегда в сторону, противоположную действию движущей силы.

Если движущая сила больше силы трения, то движение одного тела по отношению к другому будет ускоренным (второй закон Ньютона).  Если движущая сила равна «иле трения, то движение будет равномерным (по инерции).  Если движущая сила окажется меньше силы трения, то движение приостановится. 

Силы трения

Силой трения называют силу, которая возникает при движении одного тела по поверхности другого. Она всегда направлена противоположно направлению движения. Сила трения прямо пропорциональна силе нормального давления на трущиеся поверхности и зависит от свойств этих поверхностей. Законы трения связаны с электромагнитным взаимодействием, которое существует между телами.

       Различают трение внешнее и внутреннее.

       Внешнее трение возникает при относительном перемещении двух соприкасающихся твердых тел (трение скольжения или трение покоя).

       Внутреннее трение наблюдается при относительном перемещении частей одного и того же сплошного тела (например, жидкость или газ).

       Различают сухое и жидкое (или вязкое) трение.

       Сухое трение возникает между поверхностями твердых тел в отсутствие смазки.

       Жидким (вязким) называется трение между твердым телом и жидкой или газообразной средой или ее слоями.

       Сухое трение, в свою очередь, подразделяется на трение скольжения и трение качения.

Сухое трение

Первый закон сухого трения:

Минимальной силой, при которой начинается скольжение тела - называется силой трения покоя.

Fтрения покоя = KN (сила нормального давления).

 Второй закон сухого трения:

Сила трения покоя и сила трения скольжения не завитсят от площади соприкосновения трущихся тел и оказываются равносильной силе нормального давления.Подействуем на тело, лежащее на неподвижной плоскости, внешней силой  , постепенно увеличивая ее модуль. Вначале брусок будет оставаться неподвижным, значит, внешняя сила   уравновешивается некоторой силой  , направленной по касательной к трущейся поверхности, противоположной силе  . В этом случае   и есть сила трения покоя.

Установлено, что максимальная сила трения покоя не зависит от площади соприкосновения тел и приблизительно пропорциональна модулю силы нормального давления  N:

μ₀ – коэффициент трения покоя, зависящий от природы и состояния трущихся поверхностей.

       Когда модуль внешней силы, а следовательно, и модуль силы трения покоя превысит значение  F₀, тело начнет скользить по опоре – трение покоя  F_тр.пок  сменится трением скольжения  F_ск  (рис. 4.6):

Fтр = μ N,

(4.4.1)

где  μ  – коэффициент трения скольжения.

       Трение качения возникает между шарообразным телом и поверхностью, по которой оно катится. Сила трения качения подчиняется тем же законам, что и сила трения скольжения, но коэффициент трения  μ ; здесь значительно меньше.

       Подробнее рассмотрим силу трения скольжения на наклонной плоскости (рис. 4.7).

На тело, находящееся на наклонной плоскости с сухим трением, действуют три силы: сила тяжести   , нормальная сила реакции опоры     и сила сухого трения   . Сила    есть равнодействующая сил     и   ; она направлена вниз, вдоль наклонной плоскости. Из рис. 4.7 видно, что

F = mg sin α,         N = mg cos α.

 Если    – тело остается неподвижным на наклонной плоскости. Максимальный угол наклона  α  определяется из условия  (F_тр)_max = F  или  μ mg cosα = mg sinα, следовательно,  tg α_max = μ, где  μ  – коэффициент сухого трения.

F_тр = μN = mg cosα,  F = mg sinα.

       При  α > α_max  тело будет скатываться с ускорением

a = g ( sinα - μ cosα ),  F_ск = ma = F - F_тр.

  Если дополнительная сила  F_вн, направленная вдоль наклонной плоскости, приложена к телу, то критический угол  α_max  и ускорение тела будут зависеть от величины и направления этой внешней силы.

Жидкостное трение

Вязкое трение – трение при наличии смазки. Смазку обычно используют, чтобы уменьшить трение и интенсивность изнашивания, а также избавиться от некоторых нежелательных особенностей, присущих сухому трению.

Обычно в качестве смазки используют жидкость (например, смазочные масла' ); в этом случае говорят о жидкостном трении. Ныне иногда применяют и твердые смазочные материалы (графит, тефлон, молибденит), которые наносят в виде покрытий на контактирующие поверхности. Силы вязкого трения существенно зависят от относительной скорости контактирующих тел; если она равна нулю, то эти силы также обращаются в нуль. Поскольку мы сейчас занимаемся статикой, то их мы рассматривать не будем. Итак: Ограничимся случаем сухого трения. Чем вызвано наличие сухого трения? Современные представления об этом явлении таковы. Сухое трение возникает за счет механического взаимодействия между микронеровностями соприкасающихся поверхностей, а также адгезии (сцепления этих поверхностей, вызываемого межмолекулярным взаимодействием). Для деталей, обычно используемых в машиностроении, размеры упомянутых микронеровностей изменяются от долей микрометра до десятков микрометров (т.е. весьма невелики). Следовательно, сухое трение – это сложное физическое явление, вызываемое двумя факторами: механическим и адгезионным взаимодействием. Когда мы сталкиваемся с контактом двух заведомо шероховатых поверхностей, то на первый план выходят механические факторы; когда же мы пытаемся сдвинуть друг относительно друга две отполированные свинцовые пластинки, то это трудно сделать из-за эффекта адгезии. Обсудим теперь вопрос о том, какими могут быть предельные значения сил трения.

Трение качения

Тре́ние каче́ния — сопротивление движению, возникающее при перекатывании тел друг по другу. Проявляется, например, между элементами подшипников качения, между шиной колеса автомобиля и дорожным полотном. В большинстве случаев величина трения качения гораздо меньше величины трения скольжения при прочих равных условиях, и потому качение является распространенным видом движения в технике.

Трение качения возникает на границе двух тел, и поэтому оно классифицируется как вид внешнего трения.

Пусть на тело вращения, располагающееся на опоре, действуют

P — внешняя сила, пытающаяся привести тело в состояние качения или поддерживающая качение и направленная вдоль опоры;

N — прижимающая сила;

 — реакция опоры.

Если векторная сумма этих сил равна нулю

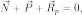
то ось симметрии тела движется равномерно и прямолинейно или остаётся неподвижной(см. рис. 1). Вектор   определяет силу трения качения, противодействующую движению. Это означает, что прижимающая сила уравновешивается вертикальной составляющей реакции опоры, а внешняя сила уравновешивается касательной составляющей реакции опоры.

.   — внешняя сила;   — сила трения качения; R — радиус тела вращения; 

Равномерное качение означает также, что сумма моментов сил относительно произвольной точки равна нулю. Из равновесия относительно оси вращения моментов сил, изображённых на рис. 2 и 3, следует:

откуда

где

 — сила трения качения;

f — коэффициент трения качения, имеющий размерность длины (следует отметить важное отличие от коэффициента трения скольжения, который безразмерен);

R — радиус катящегося тела;

N — прижимающая сила.

Момент силы трения   действующий против часовой стрелки (относительно мгновенного центра вращения в зоне контакта — правого конца отрезка f) и тормозящий качение тела вправо; N — прижимающая сила; f — коэффициент трения качения, равный длине плеча силы N.

Коэффициент трения f;   — асимметричная реакция опорной поверхности, векторная сумма вертикальной   и горизонтальной  компонент;   — прижимающая сила;   — сила трения качения.

Эта зависимость подтверждается экспериментально. Для малой скорости качения сила трения качения не зависит от величины этой скорости. Когда скорость качения достигает значений, сопоставимых со значениями скорости деформации в материале опоры, трение качения резко возрастает и даже может превысить трение скольжения при аналогичных условиях.

Определим для подвижного цилиндра момент, тормозящий вращательное движение тела. Рассматривая данный момент относительно оси вращающегося колеса (например, колеса автомобиля), находим, что он равен произведению тормозного усилия на оси на радиус колеса. Относительно точки контакта движущегося тела с землей момент будет равен произведению внешней силы, уравновешивающей силу трения, на радиус колеса (рис. 2):

.

С другой стороны, момент трения равен моменту прижимающей силы   на плечо, длина которого равна коэффициенту трения качения f:

где

 — момент силы трения в [Н] · [м];

R — радиус тела качения;

P — внешняя сила;

 — сила трения качения;

f — коэффициент трения качения в [м].

Из выписанного выше уравнения следует, что коэффициент трения качения может быть определен как отношение момента трения качения   к прижимной силе N:

Графическая интерпретация коэффициента трения качения f дана на рис. 3 и 4.

Коэффициент трения качения имеет следующие физические интерпретации:

Если тело находится в покое и внешняя сила отсутствует, то реакция опоры лежит на той же линии, что и прижимающая сила. Когда тело катится, то из условия равновесия следует, что нормальная составляющая реакции опоры параллельна и противонаправлена прижимающей силе, но не лежит с ней на одной линии. Коэффициент трения качения равен расстоянию между прямыми, вдоль которых действуют прижимающая сила и нормальная составляющая реакции опоры (рис. 4).

Движение катящегося тела без проскальзывания можно рассматривать как поворот вокруг мгновенной оси вращения (на рис. 4 — точка приложения вектора  ), которая для абсолютно твёрдых тел совпадает с основанием перпендикуляра, опущенного из центра круга на опору. Для случая реальных (деформирующихся под нагрузкой) материалов мгновенный центр вращения смещён в направлении качения тела, а величина смещения равна значению коэффициента трения качения.

Силы инерции (поступательное и вращательное движение)

Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.^[1]

 общем случае поступательное движение происходит в трёхмерном пространстве, но его основная особенность — сохранение параллельности любого отрезка самому себе, остаётся в силе.

Математически поступательное движение по своему конечному результату эквивалентно параллельному переносу.Однако, рассматриваемое как физический процесс оно представляет собой в трёхмерном пространстве вариант винтового движения

сли тело движется поступательно, то для описания его движения достаточно описать движение произвольной его точки (например, движение центра масс тела).

Одной из важнейших характеристик движения точки является её траектория, в общем случае представляющая собой пространственную кривую, которую можно представить в виде сопряжённых дуг различного радиуса, исходящего каждый из своего центра, положение которого может меняться во времени. В пределе и прямая может рассматриваться как дуга, радиус которой равен бесконечности.

В таком случае оказывается, что при поступательном движении в каждый заданный момент времени любая точка тела совершает поворот вокруг своего мгновенного центра поворота, причём длина радиуса в данный момент одинакова для всех точек тела. Одинаковы по величине и направлению и векторы скорости точек тела, а также испытываемые ими ускорения.

При решении задач теоретической механики бывает удобно рассматривать движение тела как сложение движения центра масс тела и вращательного движения самого тела вокруг центра масс (это обстоятельство принято во внимание при формулировке теоремы Кёнига).

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам.

Кинематические характеристики

Вращение твердого тела, как целого характеризуется углом  , измеряющегося в угловых градусах или радианах, угловой скоростью   (измеряется в рад/с) и угловым ускорением   (единица измерения - рад/с²).

При равномерном вращении (T оборотов в секунду),

• Частота вращения — число оборотов тела в единицу времени.

,

• Период вращения — время одного полного оборота. Период вращения T и его частота   связаны соотношением  .

• Линейная скорость точки, находящейся на расстоянии R от оси вращения

,

• Угловая скорость вращения тела

 .Динамические характеристики

Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергии вращения можно записать в виде  . В этой формуле момент инерции играет роль массы, а угловая скорость роль обычной скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы  .

• Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.