4.4.На какое расстояние от плоскости мидель-шпангоута должен быть принят груз массой 300 (т), чтобы осадка судна кормой не изменилась?

М = 4386,2 (т),значит М₁ = 4386,2 +300 = 4686,2 (т),

dк = 6,1 (м)

При dк и М: Хс = -4,56 (м), При dк и М₁: Хс₁ = -4,4 (м).

Абсцисса центра тяжести:

Х = (М₁*Хс₁-М*Хс)/m = (4686,2 *(-4,4 )- 4386,2 *(-4,56))/300 =-2,06 (м).

4.5.Определить изменения метацентрической высоты судна при заливании промысловой палубы слоем воды 0,3 (м).

Метацентрическая высота меняется из-за приема груза и из-за наличия свободной поверхности:

Длина пром.палубы=35 м.

Ширина пром.палубы-11 м.

V = L*H*0,3 = 35*16*0,3 = 168 (м³)

m = V = 1,025*168 = 172,2 (т)

М1=M+m = 4386,2+172,2 = 4558,4(т), по диаграмме посадок снимем новые

М_х1=М_х+ m*х₁= -20008,2+172,2*(-20)=-23452,2(т*м)

Xc₁ Xg₁= М_х1/ М₁=-23452,2/4558,4=-5,14(м)

dн = 3,66 (м)

dк = 6,28 (м)

d = (3,66+6,28)/2 = 4,97 (м).

d = d-d = 4,97-4,88 = 0,09(м).

0.08*35*1331=3726,8

k=1/12

h = =172,2/4558,4*(4,88+0,09/2-10,2-0,81-3726,8/168)=-1,046м.

4.6.Определить на сколько уменьшилась метацентрическая высота судна от обледенения, если период бортовой качки увеличился на 20%.

Для решения задачи воспользуемся формулой для периода бортовой качки судна: _=С*В/ («капитанская формула»), полагая, что инерционный коэффициент С до и после обледенения сохраняет своё значение (для промысловых судов он равен 0,7-0,8).

Так как : _=С*В/ , то 1,2_=С*В/ 1

Если разделить первое на второе получим: 1,2 = / 1

=1,44;

h₁= =0,81/1,44=0,56;

Изменение метацентрической высоты:

h = h₁-h = 0,56-0,81= -0,25 (м) (уменьшилась в результате обледенения).

4.7.Определяем угол крена судна на установившейся циркуляцией при скорости судна 12 уз .

Наибольший кренящий момент на циркуляции:

Мкр = 0,233* (Zg-0,5*d);

где V – скорость судна на прямом курсе;

L – длина между перпендикулярами.

Переводим узлы в м/с:

V = 12*0,514 = 6,17 (м/с)

Подставляем значения в исходную формулу:

Мкр = (0,233*4386,2 *6,17²/96,4)*( 6,94 -4,88/2)=1816,143(кН*м) ;

Угол крена на циркуляции будет равен:

 = 57,3*Мкр/М*g*h = 57,3*1816,143/4386,2 *9,8*0,81 = 2,98

4.8.Находим метацентрическую высоту судна, сидящего на мели без крена с осадками носом и кормой на 0,5 (м) меньше, чем на глубокой воде. Определить критическую осадку, при которой судно начнёт терять устойчивость.

Восстанавливающий момент судна, сидящего на мели, подсчитываем по формуле:

Мв = *(Va*Zma-V*Zg)sin = a*(Zma- /a* Zg)sin = a*ha*sin,

где V и Va – объёмное водоизмещение судна до и после посадки на мель; а=*Vа – вес вытесненной воды после посадки на мель;

=*V-вес судна;

Zma – аппликата поперечного метацентра судна, сидящего на мели.

Из формулы для Мв видно, что метацентрическая высота для судна, сидящего на мели:

ha = Zma- /a*Zg,

dк₁ = dк-0,5= 6,1-0,5=5,6 (м), dн₁ = dн -0,5=3,55-0,5=3,05 (м)

Следовательно Mа находим из приложения 2.2. по dк₁ и dн₁ то Ма=3850(т)

Вычисляем объёмные водоизмещения судна до и после посадки на мель:

V = M/ =4386,2 /1,025 = 4279,2 (м³);

Va = Ма/ = 3905/1,025 = 3809,8 (м³ ).

Находим вес вытесненной воды после посадки на мель и вес судна:

 = *V =* g*V= 10,05*4279,2 = 43005,96(кН);

а = *Vа =* g*V= 10,05*3809,8 = 38288,49(кН).

Zc₁ = 2,58(м), r₁ = 5,3 (м) следовательно Zma₁ = 2,58+5,3 = 7,88 (м)

Zc = 2,87 (м), r = 4,88 (м) следовательно Zma = 2,87+4,88= 7, 75(м)

ha = 7,88 – 43005,96/ 38288,49*6,94=-0,08 (м) .

Для определения критической осадки сводим данные в таблицу и на её основе строим график зависимости V_a Z_ma от осадки d.

Критическую осадку d_кр определяем графическим способом при V_a Z_ma=VZ_g.

V_aZ_ma от d .

d	dн	dк	Ma	va=Ma/	zca	ra	zma= zca+ ra	vazma
4,88	3,55	6,2	4386,2	4279,2	2,87	4,88	7,75	33163,3
4,68	3,35	6,0	4250,0	4146,3	2,75	5,02	7,77	32216,7
4,38	3,05	5,7	3850,0	3756,1	2,58	5,3	7,85	29409,4

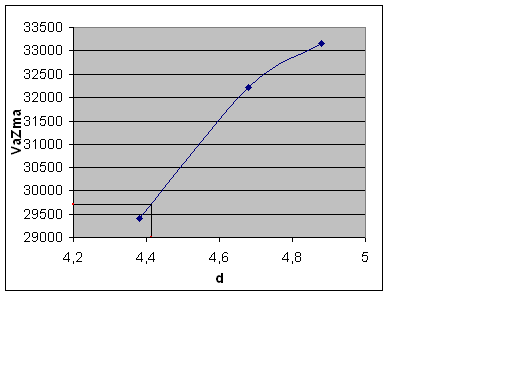
График нам показывает, что судно начнёт терять осадку когда достигнет критической осадки 4,41 м. поскольку VZ_g.=29697,6

4.9.Определяем динамические углы крена от динамически приложенного кренящего момента, от давления ветра для двух случаев положения судна. В первом случае наклонения происходят с прямого положения, во втором – судно накренено на наветренный борт на угол, равный амплитуде бортовой качки.

Динамически приложенный кренящий момент Мкр(в кН*м) подсчитывается по формуле:

Мкр = 0,001*р *S*Z (кН*м),

где р – давление ветра, Н/м²;

S – площадь парусности, м²;

Z – отстояние центра парусности от плоскости действующей ватерлинии, м.

Давление ветра р принимаем в зависимости от района плавания и плеча парусности Z. А площадь парусности S и плечо парусности Z снимаем с графика из приложения 2.9.(площадь и возвышение центра парусности) по d.

Так как d = 4.88(м), то S =1101(м²), Z=6,17(м) относительно действующей ватерлинии.

Следовательно р=1176,9 (Н/м²).

Подставив все найденные значения в формулу, получим:

Мкр = 0,001*1176,9*1101*6,17= 7994,9 (кН*м).

Амплитуду качки вычисляем по формуле:

m = k*X₁*X₂*Y,

где Х₁ и Х₂ – безразмерные множители, зависящие соответственно от отношения B/d и коэффициента общей полноты ;

Y–множитель, (град);

k – коэффициент, зависящий от отношения суммарной площади скуловых килей к произведению L*B.

Значения X₁ ,X₂ и k выбираем из таблиц в зависимости от отношения В/ d, коэффициента общей полноты  и отношения площади скуловых килей Ак к произведению L*B. Значение Y принимаем в зависимости от района плавания и отношения /В.

Так как В/d=16/4,88=3,3, то X₁=0,83.

А =V/L*B*d=4279,2 /96,4*16*4,88=0,57, тогда X₂=0,914.

Так как (Ак/ L*B)*100%=((14,2*2)/96,4*16)*100%=1,8%, следовательно k=0,9.

Найдём Y по /В=0,933/16=0,056, получим Y=26,2

Тогда, подставляя все найденные значения получим, что амплитуда качки

m = 0,9*0,83*0,914*26,2= 17,89

Динамические углы крена д при действии на судно момента Мкр находим из условия равенства работ восстанавливающего и кренящего моментов при наклонении судна в первом случае от 0 до д, во втором – от  до д. Работы восстанавливающего и кренящего моментов геометрически представляются площадями, ограниченными соответственно диаграммой статической остойчивости и кривой плеч кренящего момента, а также осью абсцисс и ординатами  и д в первом случае и m и д – во втором.

Плечо кренящего момента вычисляем по формуле:

L^д_кр = = 7994,9 /(4386,2*9,8) = 0,19(м)

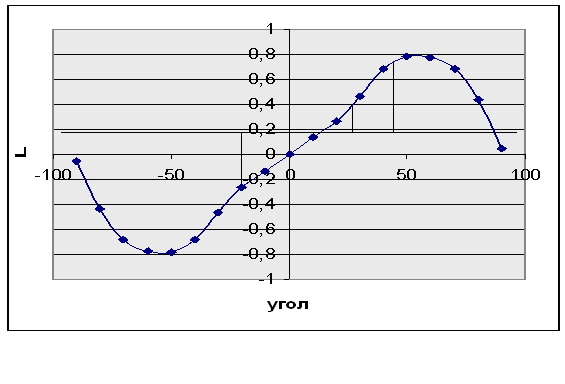
По диаграмме статической остойчивости определяем, что для первого случая д₁ = 25, для второго случая д₂ = 43