4. Алгоритм формирования хэш – функции

4.1. Понятие хэш – функции

Хэш-функция представляет собой криптографическую функцию от сообщения произвольной длины, значение которой зависит сложным образом от каждого бита сообщения.

Реализация хэш-функции обычно осуществляется в виде некото­рого итеративного механизма, который позволяет вычи­слить для сообщения М произвольной длины так называемый хэш-код H(М) фиксированного размера т (обычно т = 128, 160, 256, 384, 512 бит). Хэш-код является подобием "слепка" сообщения (дайджест сообщения, резюме сообщения), а преобразование входного массива данных в короткое число фиксированной длины т называют хэшированием.

Простым примером хэширования может служить нахождение циклической контрольной суммы: сначала суммируются коды символов, входящих в текст сообщения, а затем отбрасываются все цифры, за исключением нескольких последних. Полученное число в данном случае является примером хэш-кода исходного текста.

Широкое применение на практике хэш-функции получили в криптографии (криптостойкие хэш-функции), в частности, в системах электронной цифровой подписи (ЭЦП). Использование хэш-функции в системах ЭЦП позволяет упростить проблему подписи сообщений (документов) большого объема (длиной более 32 кбит).

При прямолинейном использовании механизма двухключевой криптографии блоки данных, которые могут быть подписаны непосредственно, ограничены по размеру: они не могут выходить за пределы используемой при работе алгоритмов разрядной сетки. Поэтому, если сообщение имеет большой размер, то его необходимо разбить на большое число блоков меньшего размера и выработать столько подписей сколько блоков будет содержаться в сообщении, что сильно усложняет проблему хранения подписей и самих подписанных сообщений, а также организацию баз данных, содержащих большое число подписанных документов. Чтобы преодолеть данное ограничение и упростить данную проблему, принято подписывать не непосредственно электронный документ, а некоторый его цифровой образ небольшого фиксированного размера, полученный с помощью определенного алгоритма хэшированием (хэш-функции).

Алгоритмы хэширования, или хэш-функции, помимо использования в схемах ЭЦП могут применяться и самостоятельно в схемах защиты информации. Например, с их помощью можно вырабатывать ключ шифрования из пароля.

К хэш-функциям предъявляются определенные требования, основными среди которых являются следующие:

• постоянством размера: для входного массива данных произвольного размера М результатом должен быть блок данных фиксированного размера т;

• вычислительной необратимостью: вычислительно неосуществимо нахождение сообщения M, хэш-код которого был бы равен заданному значению Н;

• свободой от коллизий: вычислительно неосуществимо нахождение двух сообщений M₁ и М₂  M₁ с равными значениями хэш-кода, т.е. удовлетворяющих условию Н(М₁ ) = Н(М₂ ).

Если эти требования не выполняются, то потенциальный злоумышленник может подделать сообщение для подписанного хэш-кода.

Хэш-функция, построенная на базе итеративного механизма, аналитически записывается в виде:

,

где Н_о – некоторое специфицированное начальное значение, Е – некоторая легко вычислимая функция шифрования, M_i - текущий блок сообщения.

Известно, что если какая-либо атака может быть предпринята против базовой функции h, то эта же атака может быть предпринята и против итеративной функции H, причем сложности атак в обоих случаях одинаковы. Это положение определяет необходимость применения криптографически стойких базовых функций, для построения которых часто используют блочные шифры.

Современные блочные шифры являются стойкими к атаке на основе известного исходного текста, поэтому если использовать блок M_i в качестве ключа (см. рисунок 4.1), то по значениям H_i-1 (входное сообщение для шифрующей функции) и H_i, (результат шифрующего преобразования) вычислительно неосуществимо нахождение значения М_i. Данную схему формирования хэш-кода можно записать как

,

где – функция преобразования значения Н под управлением М, т.е. блока сообщения.

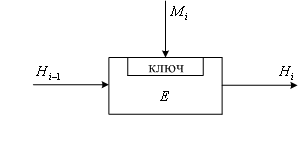
Рисунок 4.1 – Формирование хэш-кода по схеме

Однако при применении данной схемы возможны атаки, использующие «парадокс дня рождения».

«Парадокс дня рождения» заключается в вероятности совпадения дней рождения в одном коллективе как минимум у двух человек, применительно к хэш-функциям – в совпадении двух сообщений, имеющих одинаковый хэш-код, из к сообщений. При этом вероятность совпадения двух хэш-кодов (дней рождения) будет больше 0,5.

Предположим, что количество выходных значений хэш-кодов Н равно n. Тогда вероятность совпадения хэш-кодов для случайной пары сообщений Н(М₁) = Н(M_i) равна 1/n. Соответственно, вероятность того, что Н(М₁) ≠ Н(M_i), равна 1-1/n. При создании к сообщений вероятность того, что ни для одного из них не будет совпадений хэш-кодов, равна произведению вероятностей (1-1/n)^к. Следовательно, вероятность, по крайней мере, одного совпадения хэш-кодов равна 1-(1-1/n)^к. Применив упрощенную формулу бинома Ньютона получим, что к = n^1/2.

Если хэш-код имеет длину m бит, т.е. принимает 2^m значений, то , т.е. при p  0,5 имеется к = 2^m/2 сообщений, у двух из которых хэш – коды имеют одинакое значение, т.е. Н(М₁ ) = Н(M_i ).

Противник, не зная ключа шифрования, создает 2^m/2 вариантов сообщения, каждое из которых имеет некоторый определенный смысл, а также такое же количество сообщений, каждое из которых является поддельным и предназначено для замены настоящего сообщения. Два набора сообщений сравниваются в поисках пары сообщений, имеющих одинаковый хэш-код. При этом вероятность успеха в соответствии с «парадоксом дня рождения» больше 0,5. Если соответствующая пара не найдена, то создаются дополнительные исходные и поддельные сообщения до тех пор, пока не будет найдена пара. Далее атакующий предлагает отправителю исходный вариант сообщения для подписи. Эта подпись затем легко может быть присоединена к поддельному варианту для передачи получателю, поскольку оба варианта имеют один и тот же хэш-код, и, следовательно, будет создана одинаковая цифровая подпись. Легко оценить, что сложность такой атаки составляет около W  2^m/² операций шифрования m-битовых блоков. В случае т = 64 получаем W  2³²  410⁹.

Предпочтительными являются более сложные схемы формирования хэш-кода:

• схема Мейера-Матиаса (рисунок 4.2,а)

• схема Девиса-Мейера (рисунок 4.2,б)

где Е - функция блочного шифрования, а в качестве индекса указано значение, используемое в качестве ключа шифрования.

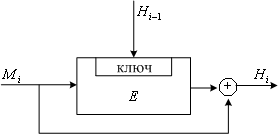
а) б)

Рисунок 4.2 – Формирование хэш-кода по схеме

Мейера-Матиаса (б) и Девиса-Мейера (б)

Однако обе эти схемы также имеют уязвимости при различных атаках.

В общем случае некоторая форма «атаки дня рождения» имеет успех при любом хэш-алгоритме, включающем использование цепочки шифрованных блоков без применения секретного ключа. Сегодня имеются различные подходы к созданию функций хэширования, а также ведутся дальнейшие исследования в данном направлении. Важным применением хэш-функции является контроль целостности информации, например программ и данных в ЭВМ. При этом, во многих случаях требуется выполнить проверку целостности больших массивов данных.

Как правило, в программных шифрах используется этап предварительных вычислений для построения ключа шифрования большой длины. Расписание использования ключа шифрования имеет динамический характер, т.е. оно зависит от входного сообщения. При построении хэш-функций на основе таких шифров существует проблема использования значения М_i или H_i в качестве ключей. Непосредственное наложение значения М_i (или H_i) как гаммы на ключ шифрования не может быть применено, т.к. при шифровании используется только часть подключей, поэтому с большой вероятностью значение хэш-функций может остаться неизменным при модифицировании сообщения М. Эта проблема может быть решена следующими путями:

1. Использование значений М_i или H_i в качестве дополнительного короткого (128-битового) ключа.

2. Применение специального преобразования основного ключа шифрования под управлением значений М_i или H_i .

3. Использование односторонних функций на основе механизмов с псевдослучайной выборкой подключей.

Второй способ не позволяет получить высокие скорости вычисления хэш-функций. Практический интерес представляют первый и третий способы, поскольку позволяют построить скоростные программные хэш-функций.