Вопрос №25. Резонанс напряжений в цепях переменного тока. Его характерные особенности. Условия возникновения и практическое значение.

Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный (Х_L) и емкостной (Х_С) элементы, при котором угол сдвига фаз  между напряжением и током равен нулю ().

Резонанс напряжений возникает на участке с последовательным соединением R,L,C. При этом индуктивное сопротивление равно емкостному, то есть .

Угол сдвига фаз  определяется по формуле:

.

При  или можно записать

Из последнего соотношения следует, что резонанс напряжения в цепи можно достигнуть следующими способами:

• изменением индуктивности L катушки;

• изменением электрической емкости С конденсатора;

• изменением частоты тока f питающей сети.

Характерные особенности резонанса напряжений:

1. Полное сопротивление Z цепи при резонансе равно активному сопротивлению

.

2. Результирующий ток в цепи имеет максимальное значение

.

Зависимость тока I от частоты f имеет вид:

3. Напряжение на участке с активным сопротивлением R равно напряжению питания U и совпадает с ним по фазе .

4. Активная мощность при резонансе имеет максимальное значение

.

Можно предположить, что в цепи существует следующее соотношение между активным (R) и реактивными сопротивлениями ( и X_C)

,

тогда можно записать

.

То есть напряжения на участках с реактивными элементами (U_L и U_C) будут больше напряжения питания U.

Свойство усиления напряжения на реактивных элементах при резонансе напряжения используется в технике.

Коэффициент усиления напряжения равен добротности Q контура

.

Однако повышенное напряжение на реактивных элементах может привести к пробою электрической изоляции проводов и представлять опасность для обслуживающего персонала.

Векторная диаграмма при резонансе напряжений строится с учетом особенностей режима резонанса

=0, ,

Вопрос № 26 Расчет цепи переменного тока с использованием комплексных чисел. Формы представления комплексного числа, их взаимосвязь.

Алгебраическая форма записи комплексного числа:

,

Тригонометрическая:

,

Показательная:

,

модуль комплексного числа:

аргумент

Вопрос №27.Свойства цепей с параллельным соединением элементов. Резонанс токов. Условия возникновения. Векторные диаграммы.

Рис. 2.13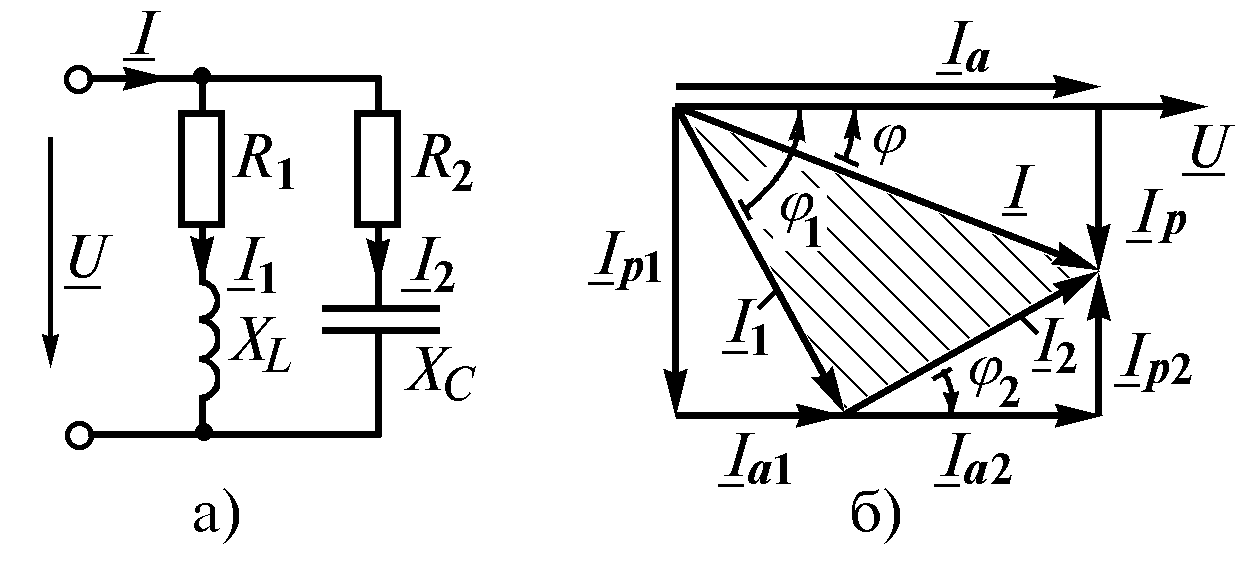

Рассмотрим цепь из двух параллельных ветвей (рис. 2.13 а). Допустим, что из­вестны напряже­ние источника и параметры схемы. Нужно определить ток , потребляемый от источника, и угол сдвига  на входе цепи. Для получения расчетных соотноше­ний построим векторную диаграмму токов. Предварительно рассчитаем токи в па­раллельных ветвях и углы их сдвига относительно приложенного напряжения. У первой ветви характер нагрузки индуктивный, ток отстает от на угол

;

;

.

У второй ветви характер нагрузки емкостный, вектор опережает на угол

;

;

.

В качестве основного вектора принимаем вектор напряжения источника , являющегося общим для двух параллельных ветвей (рис. 2.13 б). Тогда относи­тельно него нетрудно сориентировать векторы токов .

При выборе направления тока второй ветви угол откладываем от вектора в направ­лении, параллельном вектору , поскольку начала этих векторов не совме­щены. В соответствии с первым законом Кирхгофа ( ) определяем входной ток. В дальнейшем все расчетные соотношения получим из векторной диаграммы. Для этого представим каждый вектор проекциями на взаимноперпендикулярные оси. Проекцию вектора тока на вектор напряжения назовем активной составляющей тока , а перпендикулярную проекцию – реактив­ной составляющей . На диаграмме (рис. 2.13 б) эти составляющие показаны для всех векторов. Составляющие токи и физически не существуют и должны рас­сматриваться только как расчетные. По диаграмме активная составляющая вход­ного тока определяется как сумма активных составляющих токов в параллельных ветвях

(2.28)

где – активная проводимость цепи, равная арифметической сумме активных про­водимостей отдельных ветвей

где – активная проводимость -й ветви.

Только в частном случае, когда ветвь представляет собой чисто активное со­противление .

Реактивная составляющая входного тока определяется как алгебраическая сумма реактивных составляющих токов в параллельных ветвях. Реактивную со­ставляющую ветви с катушкой считают положительной, а с конденсатором – отри­цательной. Знаки учитывают при подстановке соответствующих значений

(2.29)

где – реактивная составляющая проводимости цепи, равная алгебраиче­ской сумме реактивных проводимостей отдельных ветвей.

В общем случае

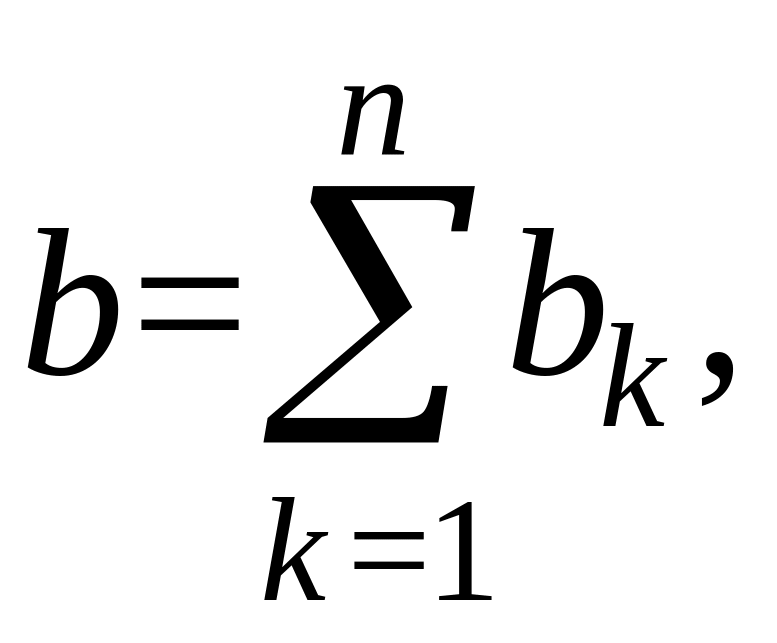
где – реактивная проводимость отдельной -й ветви,

. (2.30)

Если рассматриваемая ветвь чисто реактивная: , проводимость является обратной реактивному сопротивлению. Ток на входе цепи (см. вектор­ную диаграмму на рис. 2.13 б) с учетом (2.28, 2.29)

(2.31)

где – полная проводимость цепи, равная геометрической сумме актив­ной и реактивной проводимостей.

Угол сдвига фаз также определяется из векторной диаграммы. На рис. 2.14 а изображена векторная диаграмма входного тока , его составляющих и и напряжения источника . Треугольник, образованный вектором тока и его проекциями , и , называется треугольником токов (рис. 2.14 а). Если сто­роны этого треугольника разделить на напряжение , получится треугольник, по­добный треугольнику токов – треугольник проводимостей. Он образован проводимостями , модули которых равны соответствующим проводимо­стям, а стороны совпадают с векторами , , треугольника токов (рис. 2.14 б).

в)

На рис. 2.14 в показан треугольник проводимостей при <0. Из него нахо­дим соотношения между параметрами и формулы для определения угла сдвига фаз

; ; ; ; ; .

Чтобы учесть знак , следует использовать формулы тангенса и синуса.

В этой цепи, когда общий ток совпа­дает по фазе с напряжением, а входная реактивная проводимость или , может возникнуть явление резонанса. При противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в такой цепи получил название резонанса токов