3.3. Методические указания к выполнению лабораторных работ

По дисциплине предусмотрено выполнение лабораторного практикума. Тематика лабораторных работ охватывает вопросы исследования структурной организации и процессов функционирования арифметических устройств, устройств управления и ЭВМ в целом. В зависимости от формы обучения и объема занятий, выделенных на проведение лабораторных работ, содержание программы работ может варьироваться.

При выполнении работ № 1 и № 2 используются моделирующие программы ALU_V16.EXE (или ALU3.EXE) и MUP.EXE, расположенные на учебном сайте СЗТУ, а также в разделе сайта www.ord.com.ru/files/org_evm. Варианты заданий к этим работам следует получить у преподавателя. Примеры заданий можно найти по той же ссылке www.ord.com.ru/files/org_evm.

Лабораторная работа № 1

Исследование структуры и принципа действия двоичного арифметического устройства

1. Цель работы

Исследование работы двоичного арифметического устройства, выполняющего операции над двоичными числами с фиксированной запятой.

2. Основные теоретические положения

Арифметические устройства (АУ) предназначаются для переработки информации в ЭВМ. В состав АУ входят сумматор, регистры и ряд вспомогательных элементов и узлов.

В зависимости от типа используемого сумматора (комбинационного или накапливающего) структура АУ и алгоритмы выполнения операций в нем имеют некоторые различия. Так, в АУ на основе накапливающего сумматора обычно имеются еще два регистра. Микрооперации сдвига выполняются непосредственно в сумматоре и регистрах, преобразования кодов (из прямого в обратный и наоборот) могут осуществляться непосредственно в сумматоре и при передаче операндов из регистров в сумматор. Значения знаковых и других разрядов операндов, определяющих ход выполнения операции (например, значения разрядов множителя), анализируются непосредственно по месту хранения операндов.

В состав АУ на основе комбинационного сумматора, помимо собственно сумматора, входят еще три-четыре регистра. Микрооперации сдвига, как правило, осуществляются в специальном узле – сдвигателе, преобразования кодов выполняются только при передаче чисел из регистров в сумматор. Значения знаковых и других, необходимых по ходу выполнения операции разрядов анализируются обычно лишь на выходных шинах сумматора или вспомогательных регистров, временно сохраняющих значения выходных сигналов сумматора. Для этого операнды подаются на один из выходов сумматора при нулевом коде, поданном на его второй вход (передача транзитом). Типичная структура АУ на основе комбинационного сумматора представлена на рис. Л1.1, где Р1, Р2, Р3 – регистры; Сдв – сдвигатель; ВР – выходной (промежуточный) регистр; М1 и М2 – мультиплексоры входов 1 и 2 сумматора, позволяющие также осуществлять преобразование кодов (один или оба); ДР – дополнительный разряд (разряды) для хранения информации, выходящей при сдвигах за пределы разрядной сетки.

Д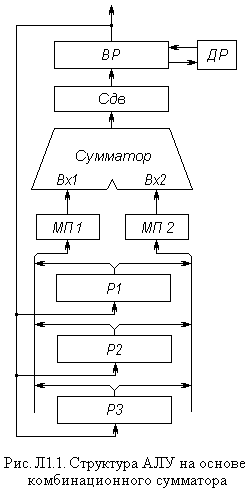 воичные числа с фиксированной запятой могут храниться как в прямом, так и в дополнительном коде памяти ЭВМ. Обработка чисел непосредственно в дополнительном коде позволяет исключать этапы предварительного преобразования кодов операндов и преобразования кода результата, в общем случае приводя к сокращению времени выполнения операции. Это сокращение оказывается особенно существенным для операций сложения и вычитания.

Рассмотрим особенности выполнения операций с помощью лабораторного макета АУ, построенного на базе комбинационного сумматора (рис. Л1.2). Алгоритм сложения двоичных чисел с фиксированной запятой, представленных в прямом коде, включает следующие шаги:

• анализ знака первого слагаемого и преобразование его в обратный (дополнительный) код, если слагаемое отрицательное;

• анализ знака и преобразование кода второго слагаемого;

• суммирование преобразованных кодов;

• анализ результата на переполнение разрядной сетки;

• анализ знака результата и преобразование обратного (дополнительного) кода отрицательного результата в прямой.

При использовании обратного кода необходимо сигнал переноса из знакового разряда подавать в младший разряд сумматора (циклический перенос). При использовании дополнительного кода этого не требуется.

Если необходимо выполнить операцию вычитания, то знак вычитаемого изменяется на обратный.

Сложение чисел, представленных в дополнительном коде, включает лишь третий и четвертый шаги, причем коды слагаемых преобразованиям не подвергаются.

При вычитании код вычитаемого преобразуется в дополнительный вне зависимости от знака и преобразование охватывает все разряды, включая знаковые. Это преобразование производится передачей на вход сумматора инверсных значений разрядов уменьшаемого и добавлением 1 к младшему разряду сумматора, что выполняется одновременно с подачей уменьшаемого на второй вход сумматора.

Р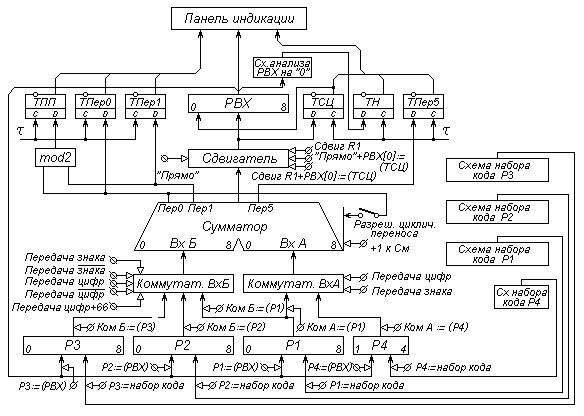 ис. Л1.2. Структурная схема макета АЛУ

Признаком переполнения разрядной сетки при наличии только одного знакового разряда в сумматоре может служить несовпадение сигналов переноса из старшего цифрового и знакового разрядов.

При умножении наиболее часто используется алгоритм умножения со сдвигом вправо суммы частичных произведений, начиная с младших разрядов множителя. Возможность реализации такого алгоритма умножения и предусматривается лабораторным макетом.

В АУ на основе комбинационного сумматора множимое, множитель и произведение (сумма частичных произведений) хранятся на отдельных регистрах. Алгоритм умножения чисел, представленных в прямом коде, включает в себя следующие шаги:

• анализ младшего разряда множителя и добавление множимого к сумме частичных произведений при единичном значении анализируемого разряда;

• сдвиг множителя и суммы частичных произведений вправо;

• определение знака произведения.

Первый и второй шаги повторяются столько раз, сколько разрядов имеет множитель. Во время их выполнения знаковый разряд множимого не принимается во внимание и не участвует в преобразовании суммы частичных произведений. Знак произведения определяется как сумма по mod2 знаков сомножителей.

Сдвиг суммы частичных произведений и множителя осуществляется поочередно посредством подачи их на один из входов сумматора с последующей передачей сигналов с его выхода через сдвигатель со сдвигом вправо на регистр, в котором хранится множитель или сумма частичных произведений.

В качестве счетчика количества повторений цикла умножения может использоваться обычный регистр, информация из которого передается через сумматор обратно в регистр, причем в момент передачи на второй вход сумматора подается обратный код единицы.

При умножении чисел, представленных в дополнительном коде, без перевода сомножителей в прямой код учитываются следующие особенности. При отрицательном множимом и положительном множителе отличие от умножения в прямых кодах состоит лишь в использовании модифицированного (с сохранением значения знакового разряда) сдвига суммы частичных произведений. Если множитель отрицателен, то независимо от знака множимого при нулевом значении анализируемого разряда множителя к сумме частичных произведений добавляется дополнение кода множимого. Перед началом операции к нулевому значению суммы частичных произведений следует добавить дополнение кода множимого, т. е. вычесть множимое. При положительных сомножителях их дополнительные коды совпадают с прямыми, поэтому отличий от умножения чисел, представленных прямыми кодами, не имеется.