20. Математическое ожидание случайной величины и его свойства. Математическое ожидание характеризует среднее ожидаемое значение случайной величины, т.Е. Приближенно равно ее среднему значению

Математическое ожидание дискретной случайной величины определяется соотношением:

, где .

Математическое ожидание непрерывной случайной величины равно

где - плотность вероятности.

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно этой величине.

.

2. Математическое ожидание суммы (разности) двух или нескольких случайных величин и равно сумме (разности) их математических ожиданий:

.

Следствие. Если – постоянная величина, то

3. Математическое ожидание произведения двух независимых случайных величин и равно произведению их математических ожиданий:

.

Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин.

Следствие. Постоянный множитель можно выносить за знак математического ожидания, т.е. .

21. Дисперсия случайной величины и ее свойства.

Дисперсией случайной величины называют математическое ожидание квадрата отклонения этой величины от ее математического ожидания.

.

Дисперсия дискретной случайной величины .

Дисперсия непрерывной случайной величины

Свойства дисперсии

1. Дисперсия постоянной величины равна нулю.

2.Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

.

3. Дисперсия суммы (разности) двух независимых случайных величин равна сумме дисперсий этих величин:

.

Если – постоянная величина, то .

Средним квадратическим отклонением случайной величины называется корень квадратный из дисперсии этой величины:

.

23. Биномиальное распределение, его математическое ожидание и дисперсия.

Закон распределения случайной величины числа появлений события в схеме Бернулли имеет вид ,

где , .

Для закона биномиального распределения вероятностей выполняется условие нормировки, т.е. сумма всех вероятностей равна единице: .

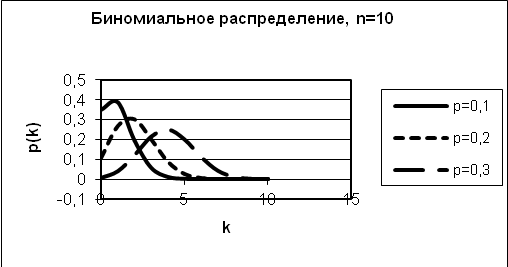
Биномиальное распределение для и некоторых значений

Математическое ожидание число появлений события в независимых испытаниях для биномиального распределения равно произведению числа испытаний на вероятность появления события в каждом испытании Дисперсия и среднее квадратическое отклонения равны соответственно:

24. Распределение Пуассона, его мат. Ожидание и дисперсия

Случайная величина называется распределенной по закону Пуассона, если она может принимать значения , соответствующая вероятность которых определяется по формуле Пуассона: ,

Распределение Пуассона для приведено ниже

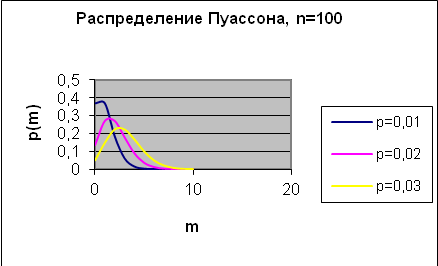
Для распределения Пуассона математическое ожидание и дисперсия равны соответственно:

.

Равенство значений математического ожидания и дисперсии является уникальным свойством распределения Пуассона. Это свойство часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина X распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики случайной величины – математическое ожидание и дисперсию. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении.