
- •1. Понятие случайного эксперимента. Пространство элементарных событий. Достоверное и невозможное событие.
- •Пространство элементарных событий.
- •2. Операции над событиями (сумма, разность, произведение). Совместные и несовместные события. Противоположное событие. Совместные и несовместные события.
- •Операции над событиями (сумма, разность, произведение).
- •3. Свойства операций над событиями.
- •4. Алгебра и сигма-алгебра событий.
- •5. Классическое определение вероятности события.
- •6. Статистическое определение вероятности события.
- •7. Геометрические вероятности.
- •Аксиоматическое построение теории вероятностей.
- •8. Понятие о полной группе событий.
- •9. Формула сложения вероятностей для совместных и несовместных событий
- •10. Условная вероятность. Формула умножения вероятностей. Независимость событий.
- •Формула умножения вероятностей.
- •Независимость событий.
- •11. Формула полной вероятности.
- •12. Формула Байеса
- •13. Основные понятия комбинаторики. Правила суммы и произведения. Перестановки, размещения, сочетания и формулы для их вычисления.
- •Правила суммы и произведения.
- •14. Схема независимых испытаний Бернулли. Наивероятнейшее число наступления событий в схеме Бернулли.
- •15. Теорема Пуассона.
- •16. Локальная теорема Муавра –Лапласа.
- •17. Интегральная (глобальная) теорема Муавра – Лапласа.
- •18. Случайная величина и ее функция распределения. Свойства функции распределения.
- •19. Непрерывные и дискретные случайные величины.
- •Закон распределения дискретной случайной величины.
- •20. Математическое ожидание случайной величины и его свойства. Математическое ожидание характеризует среднее ожидаемое значение случайной величины, т.Е. Приближенно равно ее среднему значению
- •21. Дисперсия случайной величины и ее свойства.
- •23. Биномиальное распределение, его математическое ожидание и дисперсия.
- •24. Распределение Пуассона, его мат. Ожидание и дисперсия
- •25. Равномерное распределение, его мат. Ожидание и дисперсия.
- •26. Показательное распределение, его мат.Ожидание и дисперсия.
- •27. Нормальное распределение. Свойства функции Гаусса
- •Свойства функции Гаусса.
- •28. Функция Лапласа и ее свойства. Вероятность попадания нормальной случайной величины в заданный интервал.
- •Функция Лапласа и ее свойства.
- •29. Отклонение нормальной случайной величины от ее математического ожидания. Правило «трех сигм».
- •30. Совместная функция распределения двух случайных величин. Независимые случайные величины. Мат. Ожидание и дисперсия независимых случайных величин.
- •Свойства совместной функции распределения двух случайных величин
- •Независимые случайные величины
- •Для независимых случайных величин справедливы соотношения
- •31. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины и ее свойства.
- •Свойства двумерной плотности вероятности
- •32. Корреляционный момент и коэффициент корреляции.
- •Выборочный метод и его основные понятия. Случайная выборка, объем выборки.
- •34. Вариационный ряд для дискретных и непрерывных случайных величин. Полигон и гистограмма.
- •35. Эмпирическая функция распределения и ее свойства.
- •36. Статистические оценки параметров распределения. Состоятельность и несмещенность статистических оценок.
- •37. Выборочные среднее и дисперсия.
- •38. Надежность и доверительный интервал.
- •39. Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
- •40. Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии.
- •41. Доверительный интервал для оценки среднего квадратического отклонения нормального распределения.
- •42. Проверка статистических гипотез. Нулевая и альтернативная гипотезы, статистический критерий. Ошибки первого и второго рода.
- •43. Этапы проверки статистической гипотезы.
- •44. Критерий согласия Пирсона о виде распределения.
- •45. Понятие о регрессионной зависимости случайных величин. Парная и множественная регрессии.
- •46. Выборочные уравнения регрессии.
- •47. Линейная регрессия. Нахождение коэффициентов линейной регрессии методом наименьших квадратов.
- •48. Понятие о множественной линейной регрессии.
- •49. Корреляционная матрица.
- •54. Нелинейная регрессия. Логарифмическая, обратная, степенная, и показательные модели нелинейной регрессии.
- •55. Понятие о цепях Маркова. Однородные цепи Маркова. Переходные вероятности. Матрица перехода.
- •56. Равенство Маркова. Расчет вероятностей состояния системы с использованием матрицы перехода.
- •57. Понятие о цепях Маркова с непрерывным временем.
- •58. Уравнения Колмогорова. Финальные вероятности цепей Маркова с непрерывным временем.
- •59. Понятие о схеме гибели и размножения. Расчет вероятностей состояний.
- •60. Понятие о системах массового обслуживания.
7. Геометрические вероятности.
Чтобы преодолеть недостаток классического определения вероятности, связанный с его неприменимостью к испытаниям с бесконечным числом исходов, вводят понятие геометрической вероятности – вероятности попадания точки в некоторую область ( отрезок, часть плоскости и т.д.).
В
подобных случаях пространство элементарных
исходов может быть представлено областью
![]() ,
а под событием
можно понимать исходы, входящие в
некоторую область
,
а под событием
можно понимать исходы, входящие в
некоторую область
![]() ,
принадлежащую области
.
,
принадлежащую области
.
Пусть на область наугад бросается “точка”. Какова вероятность того, что эта точка попадет в область , являющуюся частью области ?
Пусть отрезок длины
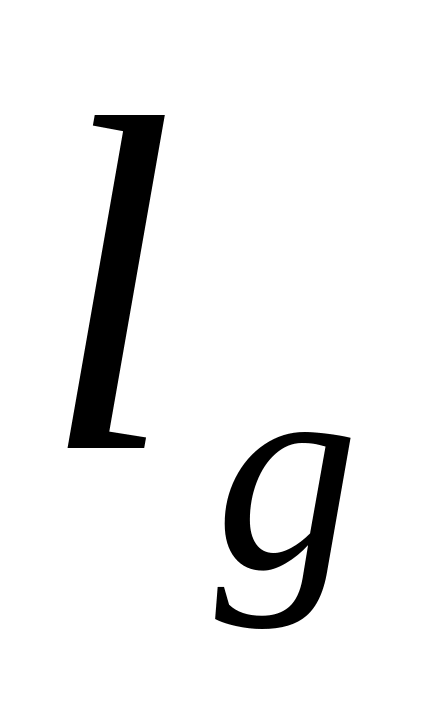 ,
составляет часть отрезка
длина которого
,
составляет часть отрезка
длина которого
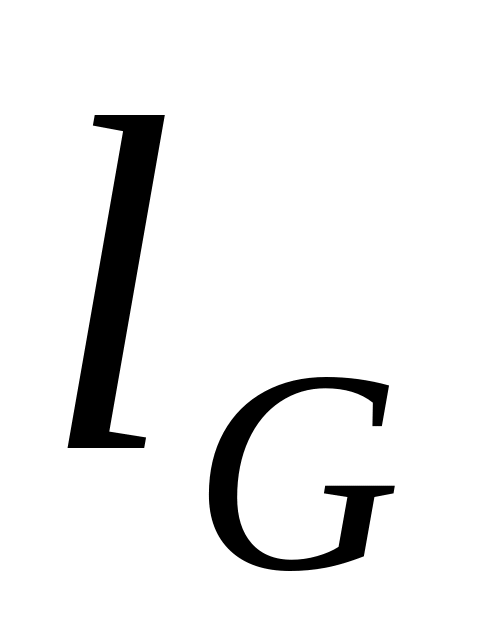 .
На отрезок
наудачу поставлена точка. Предполагается,
что
.
На отрезок
наудачу поставлена точка. Предполагается,
что
поставленная точка может оказаться в любой точке отрезка ;
вероятность попадания точки на отрезок пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка .
Тогда
вероятность попадания точки на отрезок
определяется равенством ![]() .
.
Пусть плоская фигура с площадью
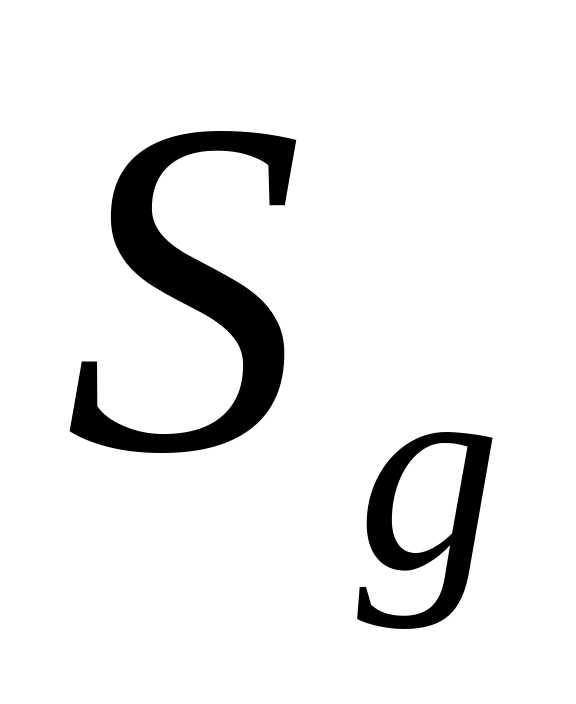 составляет часть плоской фигуры
,
площадь которой
составляет часть плоской фигуры
,
площадь которой
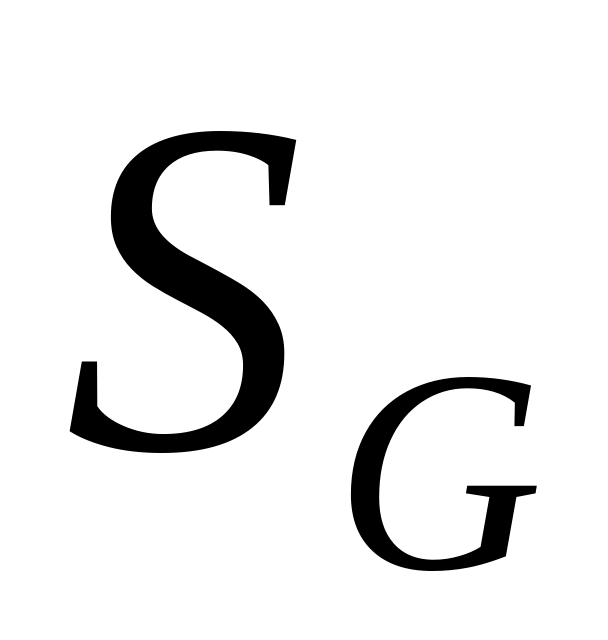 .
На фигуру
наудачу брошена точка. Предполагается,
что:
.
На фигуру
наудачу брошена точка. Предполагается,
что:
брошенная точка может оказаться в любой точке фигуры ;
вероятность попадания брошенной точки на фигуру пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно фигуры , ни от формы .
В
этих предположениях вероятность
попадания точки на фигуру
определяется равенством
![]() .
.
Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область объема
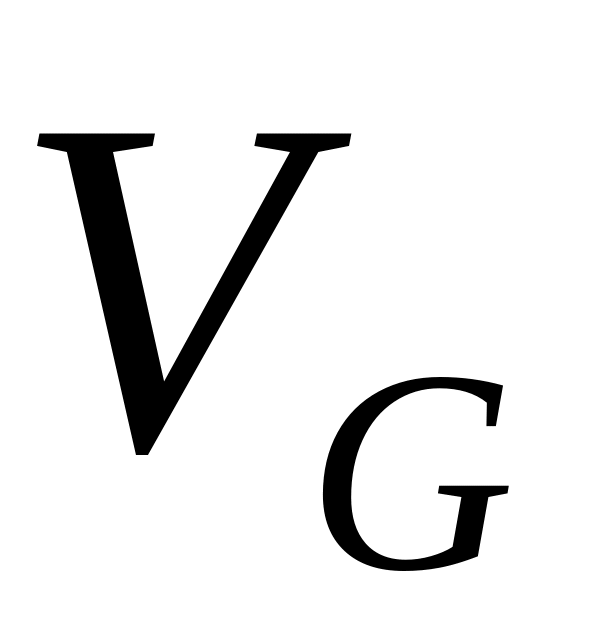 ,
содержащую область
объема
,
содержащую область
объема
![]() :
:![]()
В
общем случае понятие геометрической
вероятности вводится следующим образом.
Обозначим меру области
(длину, площадь, объем и т.д.) через
![]() ,
а меру области
– через
,
а меру области
– через
![]() .
Тогда вероятность попадания в область
точки, брошенной в область
,
определяется формулой:
.
Тогда вероятность попадания в область
точки, брошенной в область
,
определяется формулой:
![]() .
.
Пример: в течение суток к причалу могут подойти 2 парохода. Время прихода обоих пароходов независимо и равновозможно в течение суток. Определить вероятность того, что одному из пароходов придется ждать, если время разгрузки одного ид них равно 1 часу, а другого – 2 часам.
Аксиоматическое построение теории вероятностей.
Построение логически полноценной теории вероятностей основано на аксиоматическом определении случайного события и его вероятности. В системе аксиом, предложенной А.Н. Колмогоровым, элементарное событие и вероятность являются неопределяемыми понятиями. Приведем аксиомы системы Колмогорова
Каждому событию A поставлено в соответствие неотрицательное действительное число P(A). Это число называется вероятностью события A;
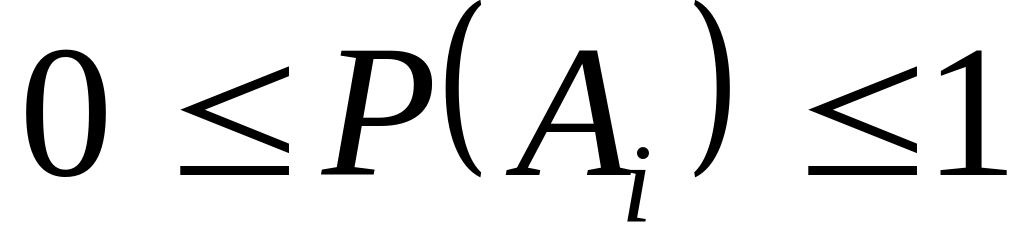
Вероятность достоверного события равна единице

Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий;
 (конечное
пространство элементарных событий)
(конечное
пространство элементарных событий)
![]() (бесконечное
пространство элементарных событий)
(бесконечное
пространство элементарных событий)
Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем.
Вероятностное пространство
Будем говорить, что задано вероятностное пространство, если задано пространство элементарных исходов , сигма алгебра и для каждого элементарного события задана его вероятность.
![]()
Иначе
говоря, Вероятностным
пространством
называется тройка (![]() ,
где
,
где
![]() - вероятностная мера на
- вероятностная мера на
![]() .
.
