42. Проверка статистических гипотез. Нулевая и альтернативная гипотезы, статистический критерий. Ошибки первого и второго рода.

Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Примеры статистических гипотез: генеральная совокупность распределена по закону Пуассона; дисперсии двух нормальных распределений равны между собой.

Нулевой (основной) называют выдвинутую гипотезу .

Альтернативной (конкурирующей) называют гипотезу , которая противоречит нулевой.

Простой называют гипотезу, содержащую только одно предположение. Например, если – параметр показательного распределения, то гипотеза – простая. Сложной называют гипотезу, состоящую из конечного или бесконечного числа простых гипотез.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Вероятность совершить ошибку первого рода принято обозначать через ; ее называют уровнем значимости.

Статистическим критерием (или просто критерием) называют случайную величину (обозначим ее через K), которая служит для проверки нулевой гипотезы. Например, если проверяют гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей, то в качестве критерия K принимают отношение исправленных выборочных дисперсий . Наблюдаемым значением критерия K_набл называют значение критерия, вычисленное по выборкам.

43. Этапы проверки статистической гипотезы.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если области принятия гипотезы – гипотезу принимают.

Различают одностороннюю (правостороннюю и левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством , где – положительное число.

Левосторонней называют критическую область, определяемую неравенством , где – отрицательное число.

Двусторонней называют критическую область, определяемую неравенствами , где . В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами или равносильным неравенством .

Этапы:

• Формулируется нулевая гипотеза ;

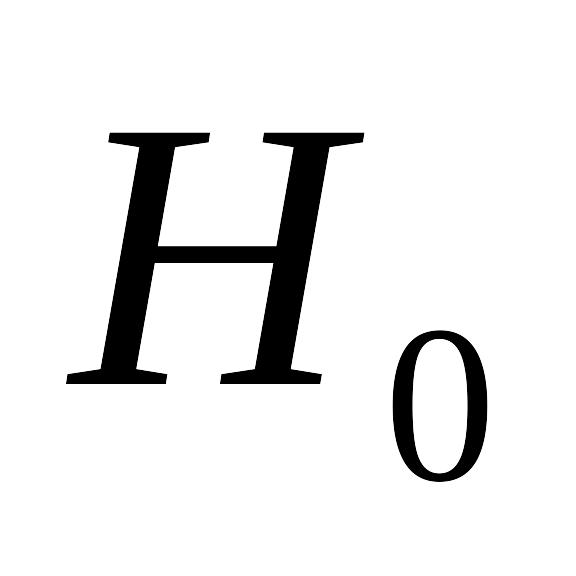• Определяется критерий K, по значениям которого можно будет принять или отвергнуть и выбирается уровень значимости ;

• По уровню значимости определяется критическая область;

По выборке вычисляется значение критерия K, определяется, принадлежит ли оно критической области и на основании этого принимается или .

44. Критерий согласия Пирсона о виде распределения.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения

Если закон распределения неизвестен, но есть основания предполагать, что он имеет определенный вид А, то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А. проверка по критерию согласия.

В качестве критерия проверки нулевой гипотезы примем случайную величину:

критерий характеризует близость эмпирич. и теор. распределений. Сам критерий называется критерием согласия X^2.

Число степеней свободы определяется из равенства , где s – число групп (частичных интервалов) выборки, r – число параметров предполагаемого распределения. . В частности, если предполагаемое распределение – нормальное, то оценивают два параметра (МО и СКО), поэтому число степеней свободы .

Построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости :

.

Таким образом, правосторонняя критическая область определяется неравенством , а область принятия нулевой гипотезы – соответственно неравенством . Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу H₀: генеральная совокупность распределена нормально, необходимо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия и по таблице критических точек распределения , по заданному уровню значимости  и числу степеней свободы k=n–3 найти критическую точку . Если – нет оснований отвергать нулевую гипотезу.

Правило проверки нулевой гипотезы: Объем выборки должен быть достаточно велик (не менее 50). Каждая группа должна содержать не менее 5–8 вариант, а малочисленные группы следует объединять в одну, суммируя частоты.

Поскольку возможны ошибки первого и второго рода, следует проявлять осторожность. Например, можно повторить опыт, увеличить число наблюдений, построить предварительно график распределения и т.п.